Published online by Cambridge University Press: 10 March 2017
The flow in a split cylinder with each half in exact counter rotation is studied numerically. The exact counter rotation, quantified by a Reynolds number  $\mathit{Re}$ based on the rotation rate and radius, imparts the system with an
$\mathit{Re}$ based on the rotation rate and radius, imparts the system with an  $O(2)$ symmetry (invariance to azimuthal rotations as well as to an involution consisting of a reflection about the mid-plane composed with a reflection about any meridional plane). The
$O(2)$ symmetry (invariance to azimuthal rotations as well as to an involution consisting of a reflection about the mid-plane composed with a reflection about any meridional plane). The  $O(2)$ symmetric basic state is dominated by a shear layer at the mid-plane separating the two counter-rotating bodies of fluid, created by the opposite-signed vortex lines emanating from the two endwalls being bent to meet at the split in the sidewall. With the exact counter rotation, the additional involution symmetry allows for steady non-axisymmetric states, that exist as a group orbit. Different members of the group simply correspond to different azimuthal orientations of the same flow structure. Steady states with azimuthal wavenumber
$O(2)$ symmetric basic state is dominated by a shear layer at the mid-plane separating the two counter-rotating bodies of fluid, created by the opposite-signed vortex lines emanating from the two endwalls being bent to meet at the split in the sidewall. With the exact counter rotation, the additional involution symmetry allows for steady non-axisymmetric states, that exist as a group orbit. Different members of the group simply correspond to different azimuthal orientations of the same flow structure. Steady states with azimuthal wavenumber  $m$ (the value of
$m$ (the value of 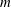 $m$ depending on the cylinder aspect ratio
$m$ depending on the cylinder aspect ratio  $\unicode[STIX]{x1D6E4}$) are the primary modes of instability as
$\unicode[STIX]{x1D6E4}$) are the primary modes of instability as 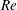 $\mathit{Re}$ and
$\mathit{Re}$ and 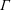 $\unicode[STIX]{x1D6E4}$ are varied. Mode competition between different steady states ensues, and further bifurcations lead to a variety of different time-dependent states, including rotating waves, direction-reversing waves, as well as a number of slow–fast pulse waves with a variety of spatio-temporal symmetries. Further from the primary instabilities, the competition between the vortex lines from each half-cylinder settles on either a
$\unicode[STIX]{x1D6E4}$ are varied. Mode competition between different steady states ensues, and further bifurcations lead to a variety of different time-dependent states, including rotating waves, direction-reversing waves, as well as a number of slow–fast pulse waves with a variety of spatio-temporal symmetries. Further from the primary instabilities, the competition between the vortex lines from each half-cylinder settles on either a 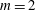 $m=2$ steady state or a limit cycle state with a half-period-flip spatio-temporal symmetry. By computing in symmetric subspaces as well as in the full space, we are able to unravel many details of the dynamics involved.
$m=2$ steady state or a limit cycle state with a half-period-flip spatio-temporal symmetry. By computing in symmetric subspaces as well as in the full space, we are able to unravel many details of the dynamics involved.