Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-22T20:43:51.824Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear Bragg scattering of surface waves over a two-dimensional periodic structure

Published online by Cambridge University Press:  04 August 2022

D.Z. Ning ,
S.B. Zhang ,
L.F. Chen Open the ORCID record for L.F. Chen [Opens in a new window] ,
H.-W. Liu  and
B. Teng
D.Z. Ning
Affiliation:
State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, PR China
S.B. Zhang
Affiliation:
State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, PR China
L.F. Chen*
Affiliation:
State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, PR China Oceans Graduate School, Faculty of Engineering and Mathematical Sciences, University of Western Australia, Crawley, WA 6009, Australia
H.-W. Liu
Affiliation:
School of Naval Architecture and Maritime, Zhejiang Ocean University, Zhoushan 316022, PR China
B. Teng
Affiliation:
State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, PR China
*
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

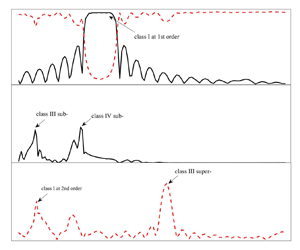
Bragg scattering of nonlinear surface waves over a wavy bottom is studied using two-dimensional fully nonlinear numerical wave tanks (NWTs). In particular, we consider cases of high nonlinearity which lead to complex wave generation and transformations, hence possible multiple Bragg resonances. The performance of the NWTs is well verified by benchmarking experiments. Classic Bragg resonances associated with second-order triad interactions among two surface (linear incident and reflected waves) and one bottom wave components (class I), and third-order quartet interactions among three surface (linear incident and reflected waves, and second-order reflected/transmitted waves) and one bottom wave components (class III) are observed. In addition, class I Bragg resonance occurring for the second-order (rather than linear) transmitted waves, and Bragg resonance arising from quintet interactions among three surface and two bottom wave components, are newly captured. The latter is denoted class IV Bragg resonance which magnifies bottom nonlinearity. It is also found that wave reflection and transmission at class III Bragg resonance have a quadratic rather than a linear relation with the bottom slope if the bottom size increases to a certain level. The surface wave and bottom nonlinearities are found to play opposite roles in shifting the Bragg resonance conditions. Finally, the results indicate that Bragg resonances are responsible for the phenomena of beating and parasitic beating, leading to a significantly large local free surface motion in front of the depth transition.

JFM classification

Waves/Free-surface Flows: Surface gravity waves Waves/Free-surface Flows: Wave scattering
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 946 , 10 September 2022 , A25
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anbarsooz, M., Passandideh-Fard, M. & Moghiman, M. 2013 Fully nonlinear viscous wave generation in numerical wave tanks. Ocean Engng 59, 73–85.CrossRefGoogle Scholar
Bailard, J.A., DeVries, J.W. & Kirby, J.T. 1992 Considerations in using Bragg reflection for storm erosion protection. ASCE J. Waterway Port Coastal Ocean Engng 118 (1), 62–74.CrossRefGoogle Scholar
Brebbia, C.A. & Walker, S. 2016 Boundary Element Techniques in Engineering. Elsevier.Google Scholar
Brorsen, M. & Larsen, J. 1987 Source generation of nonlinear gravity waves with the boundary integral equation method. Coast. Engng 11 (2), 93–113.CrossRefGoogle Scholar
Chamberlain, P.G. & Porter, D. 1995 The modified mild-slope equation. J. Fluid Mech. 291, 393–407.CrossRefGoogle Scholar
Chen, L.-F., Ning, D.-Z., Teng, B. & Zhao, M. 2017 Numerical and experimental investigation of nonlinear wave-current propagation over a submerged breakwater. J. Engng Mech. 143 (9), 04017061.Google Scholar
Christou, M., Swan, C. & Gudmestad, O.T. 2008 The interaction of surface water waves with submerged breakwaters. Coast. Engng 55 (12), 945–958.CrossRefGoogle Scholar
Davies, A.G. 1982 a On the interaction between surface waves and undulations on the seabed. J. Mar. Res. 40 (2), 331–368.Google Scholar
Davies, A.G. 1982 b The reflection of wave energy by undulations on the seabed. Dyn. Atmos. Oceans 6 (4), 207–232.CrossRefGoogle Scholar
Davies, A.G., Guazzelli, E. & Belzons, M. 1989 The propagation of long waves over an undulating bed. Phys. Fluids A 1 (8), 1331–1340.CrossRefGoogle Scholar
Davies, A.G. & Heathershaw, A.D. 1984 Surface-wave propagation over sinusoidally varying topography. J. Fluid Mech. 144, 419–443.CrossRefGoogle Scholar
Dick, T.M. & Brebner, A. 1969 Solid and permeable submerged breakwaters. In Coastal Engineering 1968, pp. 1141–1158. American Society of Civil Engineers.CrossRefGoogle Scholar
Gao, J., Ma, X., Dong, G., Chen, H., Liu, Q. & Zang, J. 2021 Investigation on the effects of Bragg reflection on harbor oscillations. Coast. Engng 170, 103977.CrossRefGoogle Scholar
Grue, J. 1992 Nonlinear water waves at a submerged obstacle or bottom topography. J. Fluid Mech. 244, 455–476.CrossRefGoogle Scholar
Hansen, J.B. & Svendsen, A. 1974 Laboratory generation of waves of constant form. Coast. Engng. 1, 321–339.Google Scholar
Heathershaw, A.D. 1982 Seabed-wave resonance and sand bar growth. Nature 296 (5855), 343–345.CrossRefGoogle Scholar
Hsu, T.-W., Lin, J.-F., Hsiao, S.-C., Ou, S.-H., Babanin, A.V. & Wu, Y.-T. 2014 Wave reflection and vortex evolution in Bragg scattering in real fluids. Ocean Engng 88, 508–519.CrossRefGoogle Scholar
Huang, C.-J. & Dong, C.-M. 2002 Propagation of water waves over rigid rippled beds. ASCE J. Waterway Port Coastal Ocean Engng 128 (5), 190–201.CrossRefGoogle Scholar
Koo, W. & Kim, M.-H. 2007 Current effects on nonlinear wave-body interactions by a 2d fully nonlinear numerical wave tank. ASCE J. Waterway Port Coastal Ocean Engng 133 (2), 136–146.CrossRefGoogle Scholar
Le Méhauté, B. 2013 An Introduction to Hydrodynamics and Water Waves. Springer Science & Business Media.Google Scholar
Liu, H.-W., Li, X.-F. & Lin, P. 2019 Analytical study of Bragg resonance by singly periodic sinusoidal ripples based on the modified mild-slope equation. Coast. Engng 150, 121–134.CrossRefGoogle Scholar
Liu, H.-W. & Zhou, X.-M. 2014 Explicit modified mild-slope equation for wave scattering by piecewise monotonic and piecewise smooth bathymetries. J. Engng Maths 87 (1), 29–45.CrossRefGoogle Scholar
Liu, Y. & Yue, D.K.P. 1998 On generalized Bragg scattering of surface waves by bottom ripples. J. Fluid Mech. 356, 297–326.CrossRefGoogle Scholar
Mattioli, F. 1990 Resonant reflection of a series of submerged breakwaters. Il Nuovo Cimento C 13 (5), 823–833.CrossRefGoogle Scholar
Mei, C.C. 1985 Resonant reflection of surface water waves by periodic sandbars. J. Fluid Mech. 152, 315–335.CrossRefGoogle Scholar
Mei, C.C., Hara, T. & Naciri, M. 1988 Note on Bragg scattering of water waves by parallel bars on the seabed. J. Fluid Mech. 186, 147–162.CrossRefGoogle Scholar
Newman, J.N. 1992 The approximation of free-surface green functions. In Wave Asymptotics, p. 107. (ed. P.A. Martin & G.R. Wickham). Cambridge University Press.Google Scholar
Ning, D., Chen, L., Zhao, M. & Teng, B. 2016 Experimental and numerical investigation of the hydrodynamic characteristics of submerged breakwaters in waves. J. Coast. Res. 32 (4), 800–813.CrossRefGoogle Scholar
Ning, D.Z. & Teng, B. 2007 Numerical simulation of fully nonlinear irregular wave tank in three dimension. Intl J. Numer. Meth. Fluids 53 (12), 1847–1862.CrossRefGoogle Scholar
Ning, D.-Z., Li, Q.-X., Chen, L.-F., Zhao, M. & Teng, B. 2017 Higher harmonics induced by dual-submerged structures. J. Coast. Res. 33 (3), 668–677.Google Scholar
Ning, D.-Z., Lin, H.-X., Teng, B. & Zou, Q.-P. 2014 Higher harmonics induced by waves propagating over a submerged obstacle in the presence of uniform current. China Ocean Engng 28 (6), 725–738.CrossRefGoogle Scholar
Peng, J., Tao, A., Liu, Y., Zheng, J., Zhang, J. & Wang, R. 2019 A laboratory study of class III Bragg resonance of gravity surface waves by periodic beds. Phys. Fluids 31 (6), 067110.Google Scholar
Peng, J., Tao, A.-F., Fan, J., Zheng, J.-H. & Liu, Y.-M. 2022 On the downshift of wave frequency for Bragg resonance. China Ocean Engng 36 (1), 76–85.CrossRefGoogle Scholar
Phillips, O.M. 1960 On the dynamics of unsteady gravity waves of finite amplitude. Part 1. The elementary interactions. J. Fluid Mech. 9 (2), 193–217.CrossRefGoogle Scholar
Porter, R. & Porter, D. 2003 Scattered and free waves over periodic beds. J. Fluid Mech. 483, 129–163.CrossRefGoogle Scholar
Wen, C. & Tsai, L. 2008 Numerical simulation of Bragg reflection based on linear waves propagation over a series of rectangular seabed. China Ocean Engng 22 (1), 71.Google Scholar
Yu, J. & Howard, L.N. 2010 On higher order Bragg resonance of water waves by bottom corrugations. J. Fluid Mech. 659, 484–504.CrossRefGoogle Scholar