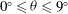Experiments on the non-Boussinesq gravity currents generated from an instantaneous buoyancy source propagating on an inclined boundary in the slope angle range $0^{\circ } \le \theta \le 9^{\circ }$ with relative density difference in the range of 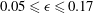$0.05 \le \epsilon \le 0.17$ are reported, where 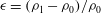$\epsilon = (\rho _1-\rho _0)/\rho _0$, with 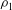$\rho _1$ and 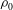$\rho _0$ the densities of the heavy and light ambient fluids, respectively. We showed that a 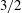$3/2$ power-law, 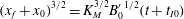${(x_f+x_0)}^{3/2}= K_M^{3/2} {B_0'}^{1/2} (t+t_{I0})$, exists between the front location measured from the virtual origin, 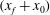$(x_f+x_0)$, and time, $t$, in the early deceleration phase for both the Boussinesq and non-Boussinesq cases, where 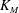$K_M$ is a measured empirical constant, 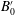$B_0'$ is the total released buoyancy, and 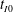$t_{I0}$ is the $t$-intercept. Our results show that 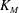$K_M$ not only increases as the relative density difference increases but also assumes its maximum value at 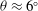$\theta \approx 6^{\circ }$ for sufficiently large relative density differences. In the late deceleration phase, the front location data deviate from the 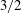$3/2$ power-law and the flow patterns on 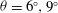$\theta =6^{\circ },9^{\circ }$ slopes are qualitatively different from those on 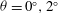$\theta =0^{\circ },2^{\circ }$. In the late deceleration phase, we showed that viscous effects could become more important and another power-law, 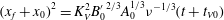${(x_f+x_0)}^{2}= K_{V}^{2} {B_0'}^{2/3} {{A}^{1/3}_0} {\nu }^{-1/3} (t+t_{V0})$, applies for both the Boussinesq and non-Boussinesq cases, where 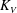$K_V$ is an empirical constant, 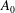$A_0$ is the initial volume of heavy fluid per unit width, $\nu $ is the kinematic viscosity of the fluids, and 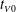$t_{V0}$ is the $t$-intercept. Our results also show that 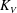$K_V$ increases as the relative density difference increases and 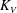$K_V$ assumes its maximum value at 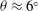$\theta \approx 6^{\circ }$.