Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T09:04:28.408Z Has data issue: false hasContentIssue false
  • English
  • Français

Near-sonic pure steam flow with real-gas effects and non-equilibrium and homogeneous condensation around thin airfoils

Published online by Cambridge University Press:  13 December 2019

Akashdeep Singh Virk Open the ORCID record for Akashdeep Singh Virk [Opens in a new window]  and
Zvi Rusak Open the ORCID record for Zvi Rusak [Opens in a new window]
Akashdeep Singh Virk
Affiliation:
Department of Mechanical, Aerospace and Nuclear Engineering, Rensselaer Polytechnic Institute, 110 8th Street, Troy, NY12180, USA
Zvi Rusak*
Affiliation:
Department of Mechanical, Aerospace and Nuclear Engineering, Rensselaer Polytechnic Institute, 110 8th Street, Troy, NY12180, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

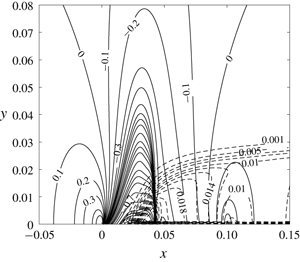
A small-disturbance asymptotic model is derived to describe the complex nature of a pure water vapour flow with non-equilibrium and homogeneous condensation around a thin airfoil operating at transonic speed and small angle of attack. The van der Waals equation of state provides real-gas relationships among the thermodynamic properties of water vapour. Classical nucleation and droplet growth theory is used to model the condensation process. The similarity parameters which determine the flow and condensation physics are identified. The flow may be described by a nonlinear and non-homogeneous partial differential equation coupled with a set of four ordinary differential equations to model the condensation process. The model problem is used to study the effects of independent variation of the upstream flow and thermodynamic conditions, airfoil geometry and angle of attack on the pressure and condensate mass fraction distributions along the airfoil surfaces and the consequent effect on the wave drag and lift coefficients. Increasing the upstream temperature at fixed values of upstream supersaturation ratio and Mach number results in increased condensation and higher wave drag coefficient. Increasing the upstream supersaturation ratio at fixed values of upstream temperature and Mach number also results in increased condensation and the wave drag coefficient increases nonlinearly. In addition, the effects of varying airfoil geometry with a fixed thickness ratio and chord on flow properties and condensation region are studied. The computed results confirm the similarity law of Zierep & Lin (Forsch. Ing. Wes. A, vol. 33 (6), 1967, pp. 169–172), relating the onset condensation Mach number to upstream stagnation relative humidity, when an effective specific heat ratio is used. The small-disturbance model is a useful tool to analyse the physics of high-speed condensing steam flows around airfoils operating at high pressures and temperatures.

JFM classification

Multiphase and Particle-laden Flows: Reacting multiphase flow Compressible Flows: Compressible Flows Compressible Flows: Shock waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 884 , 10 February 2020 , A30
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bakhtar, F. & Zidi, K. 1989 Nucleation phenomena in flowing high-pressure steam: experimental results. Proc. Inst. Mech. Engrs A 203 (3), 195–200.CrossRefGoogle Scholar
Cole, J. D. & Cook, L. P. 1986 Transonic Aerodynamics, 1st edn. North-Holland Series in Applied Mathematics and Mechanics, vol. 30. Elsevier.Google Scholar
Hamidi, S. & Kermani, M. J. 2015 Numerical study of non-equilibrium condensation and shock waves in transonic moist-air and steam flows. Aerosp. Sci. Technol. 46, 188–196.CrossRefGoogle Scholar
Head, R.1949 Investigation in spontaneous condensation phenomena. PhD thesis, California Institute of Technology, Pasadena, CA.Google Scholar
Hill, P. G. 1966 Condensation of water vapour during supersonic expansion in nozzles. J. Fluid Mech. 25 (3), 593–620.CrossRefGoogle Scholar
Krupp, J. A.1972 The numerical calculation of plane steady transonic flows past thin lifting airfoils. PhD thesis, University of Washington, Seattle, WA.CrossRefGoogle Scholar
Krupp, J. A. & Murman, E. M. 1972 Computation of transonic flows past lifting airfoils and slender bodies. AIAA J. 10 (7), 880–886.CrossRefGoogle Scholar
Lee, J.-C. & Rusak, Z. 2000 Parametric investigation of nonadiabatic compressible flow around airfoils. Phys. Fluids 13 (1), 315–323.CrossRefGoogle Scholar
Moore, M. J., Walters, P. T., Crane, R. I. & Davidson, B. J. 1973 Predicting the fog drop size in wet steam turbines. In Wet Steam 4th Conf. paper C37/73, pp. 101–109. Institution of Mechanical Engineers.Google Scholar
Moran, M. J., Shapiro, H. N., Boettner, D. D. & Bailey, M. B. 2014 Fundamentals of Engineering Thermodynamics, 8th edn. Wiley.Google Scholar
Murman, E. M. & Cole, J. D. 1971 Calculation of plane steady transonic flows. AIAA J. 9 (1), 114–121.CrossRefGoogle Scholar
Rusak, Z. 1993 Transonic flow around the leading edge of a thin airfoil with a parabolic nose. J. Fluid Mech. 248, 1–26.CrossRefGoogle Scholar
Rusak, Z. 1995 Transonic flow around optimum critical airfoils. SIAM J. Appl. Maths 55 (5), 1455–1467.CrossRefGoogle Scholar
Rusak, Z. & Lee, J.-C. 2000a Transonic flow of moist air around a thin airfoil with non-equilibrium and homogeneous condensation. J. Fluid Mech. 403, 173–199.CrossRefGoogle Scholar
Rusak, Z. & Lee, J.-C. 2000b Transonic small-disturbance theory – a tool for aerodynamic analysis and design. Can. Aeronaut. Space J. 46 (2), 74–86.Google Scholar
Rusak, Z. & Wang, C. W. 1997 Transonic flow of dense gases around an airfoil with a parabolic nose. J. Fluid Mech. 346, 1–21.CrossRefGoogle Scholar
Schmidt, B. 1966 Schallnahe Profilumströmung mit Kondensation. Acta Mechanica 2, 194–208.CrossRefGoogle Scholar
Schnerr, G. H. 1993 Transonic aerodynamics including strong effects from heat addition. Comput. Fluids 22 (2-3), 103–116.CrossRefGoogle Scholar
Schnerr, G. H. & Dohrmann, U. 1990 Transonic flow around airfoils with relaxation and energy supply by homogeneous condensation. AIAA J. 28 (7), 1187–1193.CrossRefGoogle Scholar
Schnerr, G. H. & Dohrmann, U. 1994 Drag and lift in nonadiabatic transonic flow. AIAA J. 32 (1), 101–107.CrossRefGoogle Scholar
Virk, A. S. & Rusak, Z. 2019 A small disturbance model for transonic flow of pure steam with condensation. Trans. ASME J. Fluids Engng 141 (3), 031204.CrossRefGoogle Scholar
Wagner, W. & Kretzschmar, H. J. 2007 International Steam Tables-Properties of Water and Steam based on the Industrial Formulation IAPWS-IF97: Tables, Algorithms, Diagrams, and CD-ROM Electronic Steam Tables-All of the equations of IAPWS-IF97 including a complete set of supplementary backward equations for fast calculations of heat cycles, boilers, and steam turbines, 2nd edn. Springer.Google Scholar
Wegener, P. P. 1975 Nonequilibrium flow with condensation. Acta Mechanica 21 (1–2), 65–91.CrossRefGoogle Scholar
Wegener, P. P. & Mack, L. M. 1958 Condensation in supersonic and hypersonic wind tunnels. Adv. Appl. Mech. 5, 307–447.CrossRefGoogle Scholar
Yamamoto, S. 2005 Computation of practical flow problems with release of latent heat. Energy 30 (2–4), 197–208.CrossRefGoogle Scholar
Zierep, J. 1965 Similarity laws for flows past profiles with heat influx. Acta Mechanica 1 (1), 60–70.CrossRefGoogle Scholar
Zierep, J. 1969 Transonic flow with heat input. Acta Mechanica 8 (1-2), 126–132.CrossRefGoogle Scholar
Zierep, J. & Lin, S. 1967 Bestimmung des Kondensationsbeginns bei der Entspannung feuchter Luft in Überschalldüsen. Forsch. Ing. Wes. A 33 (6), 169–172.CrossRefGoogle Scholar
Supplementary material: File

Virk and Rusak supplementary material

Virk and Rusak supplementary material

Download Virk and Rusak supplementary material(File)
File 160.9 KB