Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-23T03:01:34.845Z Has data issue: false hasContentIssue false
  • English
  • Français

A model for the electric field-driven flow and deformation of a drop or vesicle in strong electrolyte solutions

Published online by Cambridge University Press:  20 June 2022

Manman Ma ,
Michael R. Booty Open the ORCID record for Michael R. Booty [Opens in a new window]  and
Michael Siegel
Manman Ma
Affiliation:
School of Mathematical Sciences, Tongji University, Shanghai 200092, PR China
Michael R. Booty*
Affiliation:
Department of Mathematical Sciences and Center for Applied Mathematics and Statistics, New Jersey Institute of Technology, Newark, NJ 07102, USA
Michael Siegel
Affiliation:
Department of Mathematical Sciences and Center for Applied Mathematics and Statistics, New Jersey Institute of Technology, Newark, NJ 07102, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

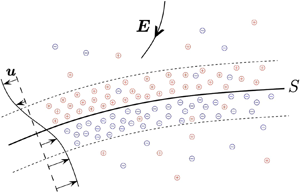
A model is constructed to describe the flow field and arbitrary deformation of a drop or vesicle that contains and is embedded in an electrolyte solution, where the flow and deformation are caused by an applied electric field. The applied field produces an electrokinetic flow, which is set up on the charge-up time scale $\tau _{*c}=\lambda _{*} a_{*}/D_{*}$, where $\lambda _{*}$ is the Debye screening length, $a_{*}$ is the inclusion length scale and $D_{*}$ is an ion diffusion constant. The model is based on the Poisson–Nernst–Planck and Stokes equations. These are reduced or simplified by forming the limit of strong electrolytes, for which dissolved salts are completely ionised in solution, together with the limit of thin Debye layers. Debye layers of opposite polarity form on either side of the drop interface or vesicle membrane, together forming an electrical double layer. Two formulations of the model are given. One utilises an integral equation for the velocity field on the interface or membrane surface together with a pair of integral equations for the electrostatic potential on the outer faces of the double layer. The other utilises a form of the stress-balance boundary condition that incorporates the double layer structure into relations between the dependent variables on the layers’ outer faces. This constitutes an interfacial boundary condition that drives an otherwise unforced Stokes flow outside the double layer. For both formulations relations derived from the transport of ions in each Debye layer give additional boundary conditions for the potential and ion concentrations outside the double layer.

JFM classification

MHD and Electrohydrodynamics: Electrokinetic flows Drops and Bubbles: Electrohydrodynamic effects Biological Fluid Dynamics: Membranes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 943 , 25 July 2022 , A47
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Allan, R.S. & Mason, S.G. 1962 Particle behaviour in shear and electric fields I. Deformation and burst of fluid drops. Proc. R. Soc. Lond. A 267, 45–61.Google Scholar
Atwater, R.P. 2020 Studies of two-phase flow with soluble surfactant. PhD thesis, New Jersey Institute of Technology.Google Scholar
Barthès-Biesel, D. 2011 Modeling the motion of capsules in flow. Curr. Opin. Colloid Interface Sci. 16, 3–12.CrossRefGoogle Scholar
Batchelor, G.K. 2000 An Introduction to Fluid Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Baygents, J.C. & Saville, D.A. 1989 The circulation produced in a drop by an electric field: a high field strength electrokinetic model. In Drops & Bubbles, Third International Colloquium, Monterey 1988 (ed. T. Wang), vol. 7, pp. 7–17. AIP Conference Proceedings, American Institute of Physics.CrossRefGoogle Scholar
Bazant, M.Z. & Squires, T.M. 2010 Induced-charge electrokinetic phenomena. Curr. Opin. Colloid Interface Sci. 15, 203–213.CrossRefGoogle Scholar
Booty, M.R. & Siegel, M. 2010 A hybrid numerical method for interfacial fluid flow with soluble surfactant. J. Comput. Phys. 229, 3864–3883.CrossRefGoogle Scholar
Chapman, D.L. 1913 A contribution to the theory of eltroencapillarity. Phil. Mag. 25, 475–481.CrossRefGoogle Scholar
Girault, H.H. 2010 Electrochemistry at liquid–liquid interfaces. In Electroanalytical Chemistry (ed. A.J. Bard & C.G. Zoski), vol. 23, pp. 1–104. CRC.CrossRefGoogle Scholar
Gouy, G. 1910 Sur la constitution de la charge électrique à la surface d'un électrolyte. J. Phys. Radium 9, 457–468.Google Scholar
Gschwend, G.C., Olaya, A., Peljo, P. & Girault, H.H. 2020 Structure and reactivity of the polarized liquid–liquid interface: what we know and what we do not. Curr. Opin. Electrochem. 19, 137–143.CrossRefGoogle Scholar
Helfrich, W. 1973 Elastic properties of lipid bilayers – theory and possible experiments. Z. Naturforsch. 28c, 693–703.CrossRefGoogle Scholar
Helmholtz, H. 1853 Ueber einige gesetze der vertheilung elektrischer ströme in körperlichen leitern mit anwendung auf die thierisch-elektrischen versuche. Ann. Phys. Chem. 165, 211–233.CrossRefGoogle Scholar
Hunter, R.J. 2001 Foundations of Colloid Science, 2nd edn. Oxford University Press.Google Scholar
Kress, R. 1999 Linear Integral Equations. Springer.CrossRefGoogle Scholar
Lacoste, D., Menon, G.I., Bazant, M.Z. & Joanny, J.F. 2009 Electrostatic and electrokinetic contributions to the elastic moduli of a driven membrane. Eur. Phys. J. E 28, 243–264.CrossRefGoogle Scholar
Mareček, V. & Samec, Z. 2017 Ion transfer kinetics at the interface between two immiscible electrolyte solutions supported on a thick-wall micro-capillary. A mini review. Curr. Opin. Electrochem. 1, 133–139.CrossRefGoogle Scholar
Melcher, J.R. & Taylor, G.I. 1969 Electrohydrodynamics: a review of the role of interfacial shear stress. Annu. Rev. Fluid Mech. 1, 111–146.CrossRefGoogle Scholar
Mori, Y., Liu, C. & Eisenberg, R.S. 2011 A model of electrodiffusion and osmotic water flow and its energetic structure. Physica D 240, 1385–1852.CrossRefGoogle Scholar
Mori, Y. & Young, Y.-N. 2018 From electrodiffusion theory to the electrohydrodynamics of leaky dielectrics through the weak electrolyte limit. J. Fluid Mech. 855, 67–130.CrossRefGoogle Scholar
Pascall, A.J. & Squires, T.M. 2011 Electrokinetics at liquid/liquid interfaces. J. Fluid Mech. 684, 163–191.CrossRefGoogle Scholar
Pozrikidis, C. 1992 Boundary Integral and Singularity Methods for Linearized Viscous Flow. Cambridge University Press.CrossRefGoogle Scholar
Rallison, J.M. & Acrivos, A. 1978 A numerical study of the deformation and burst of a viscous drop in an extensional flow. J. Fluid Mech. 89, 191–200.CrossRefGoogle Scholar
Reymond, F., Fermin, D., Lee, H.J. & Girault, H.H. 2000 Electrochemistry at liquid/liquid interfaces: methodology and potential applications. Electrochim. Acta 45, 2647–2662.CrossRefGoogle Scholar
Russel, W.B., Saville, D.A. & Schowalter, W.R. 1989 Colloidal Dispersions. Cambridge University Press.CrossRefGoogle Scholar
Samec, Z. 1988 Electrical double layer at the interface between two immiscible electrolyte solutions. Chem. Rev. 88, 617–632.CrossRefGoogle Scholar
Saville, D.A. 1997 Electrohydrodynamics: the Taylor–Melcher leaky dielectric model. Annu. Rev. Fluid Mech. 29, 27–64.CrossRefGoogle Scholar
Schnitzer, O. & Yariv, E. 2015 The Taylor–Melcher leaky dielectric model as a macroscale electrokinetic description. J. Fluid Mech. 773, 1–33.CrossRefGoogle Scholar
Schwalbe, J.T., Vlahovska, P.M. & Miksis, M.J. 2011 Vesicle electrohydrodynamics. Phys. Rev. E 83, 046309.CrossRefGoogle ScholarPubMed
Seifert, U. 1999 Fluid membranes in hydrodynamic flow fields: formalism and an application to fluctuating quasispherical vesicles in shear flow. Eur. Phys. J. B 8, 405–415.CrossRefGoogle Scholar
Squires, T.M. & Bazant, M.Z. 2004 Induced-charge electro-osmosis. J. Fluid Mech. 509, 217–252.CrossRefGoogle Scholar
Taylor, G.I. 1966 Studies in electrohydrodynamics. I. The circulation produced in a drop by an electric field. Proc. R. Soc. Lond. A 291, 159–166.Google Scholar
Vlahovska, P.M. 2019 Electrohydrodynamics of drops and vesicles. Annu. Rev. Fluid Mech. 51, 305–330.CrossRefGoogle Scholar
Vlahovska, P.M. & Gracia, R.S. 2007 Dynamics of a viscous vesicle in linear flows. Phys. Rev. E 75, 016313.CrossRefGoogle ScholarPubMed
Vlahovska, P.M., Podgorski, T. & Misbah, C. 2009 Vesicles and red blood cells in flow: from individual dynamics to rheology. C. R. Phys. 10, 775–789.CrossRefGoogle Scholar
Weatherburn, C.E. 1927 Differential Geometry of Three Dimensions, vol. 1. Cambridge University Press (Reissued 2016).Google Scholar
Woodhouse, F.G. & Goldstein, R.E. 2012 Shear-driven circulation patterns in lipid membrane vesicles. J. Fluid Mech. 705, 165–175.CrossRefGoogle Scholar
Zholkovskij, E.K., Masliyah, J.H. & Czarnecki, J. 2002 An electrokinetic model of drop deformation in an electric field. J. Fluid Mech. 472, 1–27.CrossRefGoogle Scholar