Published online by Cambridge University Press: 09 January 2013
We investigate the effect of a prescribed tangential velocity on the drag force on a circular cylinder in a spanwise uniform cross flow. Using a combination of theoretical and numerical techniques we make an attempt at determining the optimal tangential velocity profiles which will reduce the drag force acting on the cylindrical body while minimizing the net power consumption characterized through a non-dimensional power loss coefficient (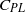 ${C}_{\mathit{PL}} $). A striking conclusion of our analysis is that the tangential velocity associated with the potential flow, which completely suppresses the drag force, is not optimal for both small and large, but finite Reynolds number. When inertial effects are negligible (
${C}_{\mathit{PL}} $). A striking conclusion of our analysis is that the tangential velocity associated with the potential flow, which completely suppresses the drag force, is not optimal for both small and large, but finite Reynolds number. When inertial effects are negligible (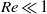 $\mathit{Re}\ll 1$), theoretical analysis based on two-dimensional Oseen equations gives us the optimal tangential velocity profile which leads to energetically efficient drag reduction. Furthermore, in the limit of zero Reynolds number (
$\mathit{Re}\ll 1$), theoretical analysis based on two-dimensional Oseen equations gives us the optimal tangential velocity profile which leads to energetically efficient drag reduction. Furthermore, in the limit of zero Reynolds number (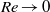 $\mathit{Re}\ensuremath{\rightarrow} 0$), minimum power loss is achieved for a tangential velocity profile corresponding to a shear-free perfect slip boundary. At finite
$\mathit{Re}\ensuremath{\rightarrow} 0$), minimum power loss is achieved for a tangential velocity profile corresponding to a shear-free perfect slip boundary. At finite 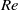 $\mathit{Re}$, results from numerical simulations indicate that perfect slip is not optimum and a further reduction in drag can be achieved for reduced power consumption. A gradual increase in the strength of a tangential velocity which involves only the first reflectionally symmetric mode leads to a monotonic reduction in drag and eventual thrust production. Simulations reveal the existence of an optimal strength for which the power consumption attains a minima. At a Reynolds number of 100, minimum value of the power loss coefficient (
$\mathit{Re}$, results from numerical simulations indicate that perfect slip is not optimum and a further reduction in drag can be achieved for reduced power consumption. A gradual increase in the strength of a tangential velocity which involves only the first reflectionally symmetric mode leads to a monotonic reduction in drag and eventual thrust production. Simulations reveal the existence of an optimal strength for which the power consumption attains a minima. At a Reynolds number of 100, minimum value of the power loss coefficient (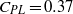 ${C}_{\mathit{PL}} = 0. 37$) is obtained when the maximum in tangential surface velocity is about one and a half times the free stream uniform velocity corresponding to a percentage drag reduction of approximately 77 %;
${C}_{\mathit{PL}} = 0. 37$) is obtained when the maximum in tangential surface velocity is about one and a half times the free stream uniform velocity corresponding to a percentage drag reduction of approximately 77 %; 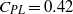 ${C}_{\mathit{PL}} = 0. 42$ and
${C}_{\mathit{PL}} = 0. 42$ and 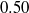 $0. 50$ for perfect slip and potential flow cases, respectively. Our results suggest that potential flow tangential velocity enables energetically efficient propulsion at all Reynolds numbers but optimal drag reduction only for
$0. 50$ for perfect slip and potential flow cases, respectively. Our results suggest that potential flow tangential velocity enables energetically efficient propulsion at all Reynolds numbers but optimal drag reduction only for 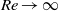 $\mathit{Re}\ensuremath{\rightarrow} \infty $. The two-dimensional strategy of reducing drag while minimizing net power consumption is shown to be effective in three dimensions via numerical simulation of flow past an infinite circular cylinder at a Reynolds number of 300. Finally a strategy of reducing drag, suitable for practical implementation and amenable to experimental testing, through piecewise constant tangential velocities distributed along the cylinder periphery is proposed and analysed.
$\mathit{Re}\ensuremath{\rightarrow} \infty $. The two-dimensional strategy of reducing drag while minimizing net power consumption is shown to be effective in three dimensions via numerical simulation of flow past an infinite circular cylinder at a Reynolds number of 300. Finally a strategy of reducing drag, suitable for practical implementation and amenable to experimental testing, through piecewise constant tangential velocities distributed along the cylinder periphery is proposed and analysed.