Published online by Cambridge University Press: 05 January 2018
We derive and assess the sharpness of analytic upper bounds for the instantaneous growth rate and finite-time amplification of palinstrophy in solutions of the two-dimensional incompressible Navier–Stokes equations. A family of optimal solenoidal fields parametrized by initial values for the Reynolds number 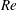 $Re$ and palinstrophy
$Re$ and palinstrophy 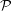 ${\mathcal{P}}$ which maximize
${\mathcal{P}}$ which maximize 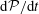 $\text{d}{\mathcal{P}}/\text{d}t$ is constructed by numerically solving suitable optimization problems for a wide range of
$\text{d}{\mathcal{P}}/\text{d}t$ is constructed by numerically solving suitable optimization problems for a wide range of 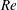 $Re$ and
$Re$ and 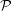 ${\mathcal{P}}$, providing numerical evidence for the sharpness of the analytic estimate
${\mathcal{P}}$, providing numerical evidence for the sharpness of the analytic estimate 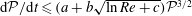 $\text{d}{\mathcal{P}}/\text{d}t\leqslant (a+b\sqrt{\ln Re+c}){\mathcal{P}}^{3/2}$ with respect to both
$\text{d}{\mathcal{P}}/\text{d}t\leqslant (a+b\sqrt{\ln Re+c}){\mathcal{P}}^{3/2}$ with respect to both 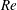 $Re$ and
$Re$ and 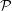 ${\mathcal{P}}$. This family of instantaneously optimal fields is then used as initial data in fully resolved direct numerical simulations, and the time evolution of different relevant norms is carefully monitored as the palinstrophy is transiently amplified before decaying. The peak values of the palinstrophy produced by these initial data, i.e.
${\mathcal{P}}$. This family of instantaneously optimal fields is then used as initial data in fully resolved direct numerical simulations, and the time evolution of different relevant norms is carefully monitored as the palinstrophy is transiently amplified before decaying. The peak values of the palinstrophy produced by these initial data, i.e. 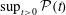 $\sup _{t>0}{\mathcal{P}}(t)$, are observed to scale with the magnitude of the initial palinstrophy
$\sup _{t>0}{\mathcal{P}}(t)$, are observed to scale with the magnitude of the initial palinstrophy 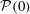 ${\mathcal{P}}(0)$ in accord with the corresponding a priori estimate. Implications of these findings for the question of finite-time singularity formation in the three-dimensional incompressible Navier–Stokes equation are discussed.
${\mathcal{P}}(0)$ in accord with the corresponding a priori estimate. Implications of these findings for the question of finite-time singularity formation in the three-dimensional incompressible Navier–Stokes equation are discussed.
Last updated 21 February 2022