Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Grandemange, M.
Gohlke, M.
and
Cadot, O.
2014.
Statistical axisymmetry of the turbulent sphere wake.
Experiments in Fluids,
Vol. 55,
Issue. 11,
Lambert, Thomas J.
Vukasinovic, Bojan
and
Glezer, Ari
2015.
Unsteady Aerodynamic Loads Effected by Flow Control on a Moving Axisymmetric Bluff Body.
Cadot, Olivier
Evrard, Antoine
and
Pastur, Luc
2015.
Imperfect supercritical bifurcation in a three-dimensional turbulent wake.
Physical Review E,
Vol. 91,
Issue. 6,
Volpe, Raffaele
Devinant, Philippe
and
Kourta, Azeddine
2015.
Experimental characterization of the unsteady natural wake of the full-scale square back Ahmed body: flow bi-stability and spectral analysis.
Experiments in Fluids,
Vol. 56,
Issue. 5,
Rigas, G.
Morgans, A. S.
Brackston, R. D.
and
Morrison, J. F.
2015.
Diffusive dynamics and stochastic models of turbulent axisymmetric wakes.
Journal of Fluid Mechanics,
Vol. 778,
Issue. ,
Oxlade, Anthony R.
Morrison, Jonathan F.
Qubain, Ala
and
Rigas, Georgios
2015.
High-frequency forcing of a turbulent axisymmetric wake.
Journal of Fluid Mechanics,
Vol. 770,
Issue. ,
p.
305.
Gentile, V.
Schrijer, F. F. J.
Van Oudheusden, B. W.
and
Scarano, F.
2016.
Low-frequency behavior of the turbulent axisymmetric near-wake.
Physics of Fluids,
Vol. 28,
Issue. 6,
Gentile, Valeria
Schrijer, Ferdinand F. J.
Van Oudheusden, Bas W.
and
Scarano, Fulvio
2016.
Proceedings of the 5th International Conference on Jets, Wakes and Separated Flows (ICJWSF2015).
Vol. 185,
Issue. ,
p.
157.
Barros, Diogo
Borée, Jacques
Noack, Bernd R.
Spohn, Andreas
and
Ruiz, Tony
2016.
Bluff body drag manipulation using pulsed jets and Coanda effect.
Journal of Fluid Mechanics,
Vol. 805,
Issue. ,
p.
422.
Brackston, R. D.
García de la Cruz, J. M.
Wynn, A.
Rigas, G.
and
Morrison, J. F.
2016.
Stochastic modelling and feedback control of bistability in a turbulent bluff body wake.
Journal of Fluid Mechanics,
Vol. 802,
Issue. ,
p.
726.
Barros, Diogo
Borée, Jacques
Noack, Bernd R.
and
Spohn, Andreas
2016.
Resonances in the forced turbulent wake past a 3D blunt body.
Physics of Fluids,
Vol. 28,
Issue. 6,
Gentile, V.
Schrijer, F. F. J.
van Oudheusden, B. W.
and
Scarano, F.
2016.
Afterbody Effects on Axisymmetric Base Flows.
AIAA Journal,
Vol. 54,
Issue. 8,
p.
2285.
Cadot, O.
2016.
Stochastic fluid structure interaction of three-dimensional plates facing a uniform flow.
Journal of Fluid Mechanics,
Vol. 794,
Issue. ,
Li, Ruiying
Barros, Diogo
Borée, Jacques
Cadot, Olivier
Noack, Bernd R.
and
Cordier, Laurent
2016.
Feedback control of bimodal wake dynamics.
Experiments in Fluids,
Vol. 57,
Issue. 10,
Varon, Eliott
Eulalie, Yoann
Edwige, Stephie
Gilotte, Philippe
and
Aider, Jean-Luc
2017.
Chaotic dynamics of large-scale structures in a turbulent wake.
Physical Review Fluids,
Vol. 2,
Issue. 3,
Yang, Jianzhi
Liu, Minghou
Wu, Guang
Gu, Hailin
and
Yao, Mengyun
2017.
On the unsteady wake dynamics behind a circular disk using fully 3D proper orthogonal decomposition.
Fluid Dynamics Research,
Vol. 49,
Issue. 1,
p.
015510.
Krol, Jakub
and
Wynn, Andrew
2017.
Dynamic reconstruction and data reconstruction for subsampled or irregularly sampled data.
Journal of Fluid Mechanics,
Vol. 825,
Issue. ,
p.
133.
García de la Cruz, Juan Marcos
Oxlade, Anthony R.
and
Morrison, Jonathan F.
2017.
Passive control of base pressure on an axisymmetric blunt body using a perimetric slit.
Physical Review Fluids,
Vol. 2,
Issue. 4,
Gentile, V.
van Oudheusden, B. W.
Schrijer, F. F. J.
and
Scarano, F.
2017.
The effect of angular misalignment on low-frequency axisymmetric wake instability.
Journal of Fluid Mechanics,
Vol. 813,
Issue. ,
Evstafyeva, O.
Morgans, A. S.
and
Dalla Longa, L.
2017.
Simulation and feedback control of the Ahmed body flow exhibiting symmetry breaking behaviour.
Journal of Fluid Mechanics,
Vol. 817,
Issue. ,
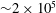 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}{\sim }2\times 10^5$. Proper orthogonal decomposition of base pressure measurements indicates that the most energetic coherent structures retain the structure of the symmetry-breaking laminar instabilities and are manifested as unsteady vortex shedding with azimuthal wavenumber
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}{\sim }2\times 10^5$. Proper orthogonal decomposition of base pressure measurements indicates that the most energetic coherent structures retain the structure of the symmetry-breaking laminar instabilities and are manifested as unsteady vortex shedding with azimuthal wavenumber 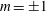 $m={\pm }1$. In a rotating reference frame, the shedding preserves the reflectional symmetry and is linked with a reflectionally symmetric mean pressure distribution on the base. Due to a slow rotation of the symmetry plane of the turbulent wake around the axis of the body, statistical axisymmetry is recovered in the time average. The ratio of the time scales associated with the slow rotation of the symmetry plane and the vortex shedding is of order 100.
$m={\pm }1$. In a rotating reference frame, the shedding preserves the reflectional symmetry and is linked with a reflectionally symmetric mean pressure distribution on the base. Due to a slow rotation of the symmetry plane of the turbulent wake around the axis of the body, statistical axisymmetry is recovered in the time average. The ratio of the time scales associated with the slow rotation of the symmetry plane and the vortex shedding is of order 100.