Published online by Cambridge University Press: 05 January 2018
This paper examines flow-separation lines on axisymmetric bodies with tapered tails, where the separating flow takes into account the effect of local body radius 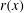 $r(x)$, incidence angle
$r(x)$, incidence angle 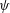 $\unicode[STIX]{x1D713}$ and the body-length Reynolds number
$\unicode[STIX]{x1D713}$ and the body-length Reynolds number  $\mathit{Re}_{L}$. The flow is interpreted as a transient problem which relates the longitudinal distance
$\mathit{Re}_{L}$. The flow is interpreted as a transient problem which relates the longitudinal distance  $x$ to time
$x$ to time 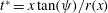 $t^{\ast }=x\,\text{tan}(\unicode[STIX]{x1D713})/r(x)$, similar to the approach of Jeans & Holloway (J. Aircraft, vol. 47 (6), 2010, pp. 2177–2183) on scaling separation lines. The windward and leeward sides correspond to the body azimuth angles
$t^{\ast }=x\,\text{tan}(\unicode[STIX]{x1D713})/r(x)$, similar to the approach of Jeans & Holloway (J. Aircraft, vol. 47 (6), 2010, pp. 2177–2183) on scaling separation lines. The windward and leeward sides correspond to the body azimuth angles 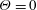 $\unicode[STIX]{x1D6E9}=0$ and
$\unicode[STIX]{x1D6E9}=0$ and 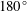 $180^{\circ }$, respectively. From China-clay flow visualisation on axisymmetric bodies and from a literature review of slender-body flows, the present study shows three findings. (i) The time scale
$180^{\circ }$, respectively. From China-clay flow visualisation on axisymmetric bodies and from a literature review of slender-body flows, the present study shows three findings. (i) The time scale 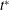 $t^{\ast }$ provides a collapse of the separation-line data,
$t^{\ast }$ provides a collapse of the separation-line data, 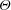 $\unicode[STIX]{x1D6E9}$, for incidence angles between
$\unicode[STIX]{x1D6E9}$, for incidence angles between 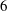 $6$ and
$6$ and 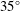 $35^{\circ }$, where the data fall on a power law
$35^{\circ }$, where the data fall on a power law  $\unicode[STIX]{x1D6E9}\sim (t^{\ast })^{k}$. (ii) The data suggest that the separation rate
$\unicode[STIX]{x1D6E9}\sim (t^{\ast })^{k}$. (ii) The data suggest that the separation rate 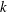 $k$ is independent of the Reynolds number over the range
$k$ is independent of the Reynolds number over the range 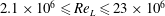 $2.1\times 10^{6}\leqslant \mathit{Re}_{L}\leqslant 23\times 10^{6}$; for a primary separation
$2.1\times 10^{6}\leqslant \mathit{Re}_{L}\leqslant 23\times 10^{6}$; for a primary separation 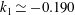 $k_{1}\simeq -0.190$, and for a secondary separation
$k_{1}\simeq -0.190$, and for a secondary separation 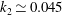 $k_{2}\simeq 0.045$. (iii) The power-law curve fits trace the primary and secondary lines to a characteristic start time
$k_{2}\simeq 0.045$. (iii) The power-law curve fits trace the primary and secondary lines to a characteristic start time 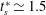 $t_{s}^{\ast }\simeq 1.5$.
$t_{s}^{\ast }\simeq 1.5$.