Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-09T20:23:29.896Z Has data issue: false hasContentIssue false
  • English
  • Français

Large-eddy simulation study of the logarithmic law for second- and higher-order moments in turbulent wall-bounded flow

Published online by Cambridge University Press:  29 September 2014

Richard J. A. M. Stevens ,
Michael Wilczek  and
Charles Meneveau
Richard J. A. M. Stevens*
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA Department of Science and Technology and J.M. Burgers Center for Fluid Dynamics, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands
Michael Wilczek
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
Charles Meneveau
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
*
†Email address for correspondence: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The logarithmic law for the mean velocity in turbulent boundary layers has long provided a valuable and robust reference for comparison with theories, models and large-eddy simulations (LES) of wall-bounded turbulence. More recently, analysis of high-Reynolds-number experimental boundary-layer data has shown that also the variance and higher-order moments of the streamwise velocity fluctuations 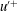$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}u^{\prime +}$ display logarithmic laws. Such experimental observations motivate the question whether LES can accurately reproduce the variance and the higher-order moments, in particular their logarithmic dependency on distance to the wall. In this study we perform LES of very high-Reynolds-number wall-modelled channel flow and focus on profiles of variance and higher-order moments of the streamwise velocity fluctuations. In agreement with the experimental data, we observe an approximately logarithmic law for the variance in the LES, with a ‘Townsend–Perry’ constant of 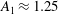$A_1\approx 1.25$. The LES also yields approximate logarithmic laws for the higher-order moments of the streamwise velocity. Good agreement is found between 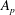$A_p$, the generalized ‘Townsend–Perry’ constants for moments of order 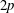$2p$, from experiments and simulations. Both are indicative of sub-Gaussian behaviour of the streamwise velocity fluctuations. The near-wall behaviour of the variance, the ranges of validity of the logarithmic law and in particular possible dependencies on characteristic length scales such as the roughness length 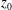$z_0$, the LES grid scale 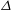$\Delta $, and subgrid scale mixing length 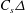$C_s\Delta $ are examined. We also present LES results on moments of spanwise and wall-normal fluctuations of velocity.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 757 , 25 October 2014 , pp. 888 - 907
Copyright
© 2014 Cambridge University Press 

References

Albertson, J. D. & Parlange, M. B. 1999 Surface length-scales and shear stress: implications for land–atmosphere interaction over complex terrain. Water Resour. Res. 35, 2121–2132.CrossRefGoogle Scholar
Alfredsson, P. H., Segalini, A. & Örlü, R. 2011 A new scaling for the streamwise turbulence intensity in wall-bounded turbulent flows and what it tells us about the ‘outer’ peak. Phys. Fluids 23, 041702.Google Scholar
Bou-Zeid, E., Meneveau, C. & Parlange, M. B. 2005 A scale-dependent Lagrangian dynamic model for large eddy simulation of complex turbulent flows. Phys. Fluids 17, 025105.Google Scholar
Brasseur, J. G. & Wei, T. 2010 Designing large-eddy simulation of the turbulent boundary layer to capture law-of-the-wall scaling. Phys. Fluids 22, 021303.CrossRefGoogle Scholar
Calaf, M., Meneveau, C. & Meyers, J. 2010 Large eddy simulations of fully developed wind-turbine array boundary layers. Phys. Fluids 22, 015110.CrossRefGoogle Scholar
Chamecki, M. & Meneveau, C. 2011 Particle boundary layer above and downstream of an area source: scaling, simulations, and pollen transport. J. Fluid Mech. 683, 1–26.CrossRefGoogle Scholar
Chester, S., Meneveau, C. & Parlange, M. B. 2007 Modeling turbulent flow over fractal trees with renormalized numerical simulation. J. Comput. Phys. 225, 427–448.Google Scholar
Eyink, G. L. 2008 Turbulent flow in pipes and channels as cross-stream ‘inverse cascades’ of vorticity. Phys. Fluids 20, 125101.Google Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2012 Turbulent pipe flow at extreme Reynolds numbers. Phys. Rev. Lett. 108 (9), 94501.Google Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2013 Logarithmic scaling of turbulence in smooth- and rough-wall pipe flow. J. Fluid Mech. 728, 376–395.Google Scholar
Hutchins, N., Chauhan, K., Marusic, I., Monty, J. P. & Klewicki, J. 2012 Towards reconciling the large-scale structure of turbulent boundary layers in the atmosphere and laboratory. Boundary-Layer Meteorol. 145 (2), 273–306.Google Scholar
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.Google Scholar
Kang, H. S., Chester, S. & Meneveau, C. 2003 Decaying turbulence in an active grid generated flow and comparisons with large eddy simulation. J. Fluid Mech. 480, 129–160.Google Scholar
Klewicki, J. C., Fife, P. & Wei, T. 2009 On the logarithmic mean profile. J. Fluid Mech. 638, 73–93.Google Scholar
Kulandaivelu, V.2012 Evolution of zero pressure gradient turbulent boundary layers from different initial conditions. PhD thesis, University of Melbourne.Google Scholar
Lenschow, D. H., Lothon, M., Mayor, S. D., Sullivan, P. P. & Canut, G. 2012 A comparison of higher-order vertical velocity moments in the convective boundary layer from lidar with in situ measurements and large-eddy simulation. Boundary-Layer Meteorol. 143, 107–123.CrossRefGoogle Scholar
Lu, H. & Porté-Agel, F. 2010 A modulated gradient model for large-eddy simulation: application to a neutral atmospheric boundary layer. Phys. Fluids 22, 015109.Google Scholar
Lu, H. & Porté-Agel, F. 2013 A modulated gradient model for scalar transport in large-eddy simulation of the atmospheric boundary layer. Phys. Fluids 25, 015110.Google Scholar
Marusic, I. & Kunkel, G. J. 2003 Streamwise turbulence intensity formulation for flat-plate boundary layers. Phys. Fluids 15, 2461–2464.Google Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010 Predictive model for wall-bounded turbulent flow. Science 329, 193–196.CrossRefGoogle ScholarPubMed
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
Meneveau, C. & Marusic, I. 2013 Generalized logarithmic law for high-order moments in turbulent boundary layers. J. Fluid Mech. 719, R1.Google Scholar
Metzger, M. M. & Klewicki, J. C. 2001 A comparative study of near-wall turbulence in high and low Reynolds number boundary layers. Phys. Fluids 13, 692–701.CrossRefGoogle Scholar
Millikan, C. M. 1938 A critical discussion of turbulent flows in channels and circular tubes. In Proceedings of the Fifth International Congress for Applied Mechanics, Harvard and MIT, 12–26 September. Wiley.Google Scholar
Moeng, C.-H. 1984 A large-eddy simulation model for the study of planetary boundary-layer turbulence. J. Atmos. Sci. 41, 2052–2062.Google Scholar
Moeng, C. H. & Rotunno, R. 1990 Vertical velocity skewness in the buoyancy-driven boundary layer. Boundary-Layer Meteorol. 47, 1149–1162.Google Scholar
Nicoud, F. & Ducros, F. 1999 Subgrid-scale stress modelling based on the square of the velocity gradient tensor. Flow Turbul. Combust. 62, 183–200.Google Scholar
Perry, A. E. & Chong, M. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.Google Scholar
Perry, A. E., Henbest, S. M. & Chong, M. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.Google Scholar
Perry, A. E., Lim, K. L. & Henbest, S. M. 1987 An experimental study of the turbulence structure in smooth- and rough-wall boundary layers. J. Fluid Mech. 177, 437–466.Google Scholar
Porté-Agel, F., Meneveau, C. & Parlange, M. B. 2000 A scale-dependent dynamic model for large-eddy simulation: application to a neutral atmospheric boundary layer. J. Fluid Mech. 415, 261–284.Google Scholar
Prandtl, L. 1925 Bericht über Untersuchungen zur ausgebildeten Turbulenz. Z. Angew. Math. Mech. 5, 136–139.Google Scholar
Schultz, M. P. & Flack, K. A. 2007 The rough-wall turbulent boundary layer from the hydraulically smooth to the fully rough regime. J. Fluid Mech. 580, 381–405.Google Scholar
Scotti, A., Meneveau, C. & Lilly, D. K. 1993 Generalized Smagorinsky model for anisotropic grids. Phys. Fluids 5, 2306–2308.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.Google Scholar
Stoll, R. & Porté-Agel, F. 2006 Effects of roughness on surface boundary conditions for large-eddy simulation. Boundary-Layer Meteorol. 118, 169–187.Google Scholar
Sullivan, P. P. & Patton, E. G. 2011 The effect of mesh resolution on convective boundary layer statistics and structures generated by large-eddy simulation. J. Atmos. Sci. 68, 2395–2415.CrossRefGoogle Scholar
Townsend, A. A. 1976 Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
von Kármán, T. 1930 Mechanische Ähnlichkeit und Turbulenz. Gött. Nachr. 68, 58–76.Google Scholar
Vreman, B., Geurts, B. & Kuerten, H. 1997 Large-eddy simulation of the turbulent mixing layer. J. Fluid Mech. 339, 357–390.Google Scholar
Wei, T., Fife, P., Klewicki, J. C. & McMurtry, P. 2005 Properties of the mean momentum balance in turbulent boundary layer, pipe and channel flows. J. Fluid Mech. 522, 303–327.Google Scholar
Winkel, E. S., Cutbirth, J. M., Ceccio, S. L., Perlin, M. & Dowling, D. R. 2012 Turbulence profiles from a smooth flat-plate turbulent boundary layer at high Reynolds number. Exp. Therm. Fluid Sci. 40, 140–149.Google Scholar
Zagarola, M. V. & Smits, A. J. 1998 Mean-flow scaling of turbulent pipe flow. J. Fluid Mech. 373, 33–79.CrossRefGoogle Scholar