Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-17T11:23:45.215Z Has data issue: false hasContentIssue false
  • English
  • Français

Isolated marginally stable geophysical vortices

Published online by Cambridge University Press:  17 July 2017

Álvaro Viúdez Open the ORCID record for Álvaro Viúdez [Opens in a new window]
Álvaro Viúdez*
Affiliation:
Department of Physical Oceanography and Technology, Institute of Marine Sciences, CSIC, Barcelona 08003, Spain
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Long-term marginal stability of a new family of isolated oceanic vortices is analysed. Sign reversal of the radial gradient of the potential vorticity anomaly, as implied by the isolation requirement, leads to vortex unsteadiness but does not break the coherence of the vortex, which remains marginally stable even for high absolute Rossby numbers 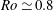$Ro\simeq 0.8$. The marginally stable vortices are characterized by a zero amount of potential vorticity anomaly on every isopycnal. The marginally stable final state is an unsteady vortex whose inner one-signed potential vorticity anomaly experiences revolution, rotation, precession and nutation.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Vortex Flows: Vortex Flows Vortex Flows: Vortex instability
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 824 , 10 August 2017 , R4
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Benilov, E. S. 2003 Instability of quasi-geostrophic vortices in a two-layer ocean with a thin upper layer. J. Fluid Mech. 475, 303–331.CrossRefGoogle Scholar
Carnevale, G. F. & Kloosterziel, R. C. 1994 Emergence and evolution of triangular vortices. J. Fluid Mech. 259, 305–331.Google Scholar
Carton, X. 2010 Oceanic vortices. In Fronts, Waves and Vortices in Geophysical Flows (ed. Flór, J.-B.), Lecture Notes in Physics, vol. 805, pp. 61–108. Springer.Google Scholar
Charney, J. G. & Stern, M. E. 1962 On the stability of internal baroclinic jets in a rotating atmosphere. J. Atmos. Sci. 19, 159–172.Google Scholar
Dritschel, D. G. & Viúdez, A. 2003 A balanced approach to modelling rotating stably-stratified geophysical flows. J. Fluid Mech. 488, 123–150.CrossRefGoogle Scholar
Hua, B. L., Ménesguen, C., Gentil, S. L., Schopp, R., Marsset, B. & Aiki, H. 2013 Layering and turbulence surrounding an anticyclonic oceanic vortex: in situ observations and quasi-geostrophic numerical simulations. J. Fluid Mech. 731, 418–442.Google Scholar
McWilliams, J. C., Graves, L. P. & Montgomery, M. T. 2003 A formal theory for vortex Rossby waves and vortex evolution. Geophys. Astrophys. Fluid Dyn. 97, 275–309.Google Scholar
Meunier, T., Ménesguen, C., Schopp, R. & Le Gentil, S. 2015 Tracer stirring around a meddy: the formation of layering. J. Phys. Oceanogr. 45, 407–423.Google Scholar
Montgomery, M. T. & Kallenbach, R. J. 1997 A theory for vortex Rossby-waves and its applications to spiral bands and intensity changes in hurricanes. Q. J. R. Meteorol. Soc. 123, 435–446.Google Scholar
Morel, Y. G. & Carton, X. J. 1994 Multipolar vortices in two-dimensional incompressible flows. J. Fluid Mech. 267, 23–51.CrossRefGoogle Scholar
Nguyen, H. Y., Hua, B. L., Schopp, R. & Carton, X. 2012 Slow quasigeostrophic unstable modes of a lens vortex in a continuously stratified flow. Geophys. Astrophys. Fluid Dyn. 106 (3), 305–319.Google Scholar
Paillet, J., Cann, B. L., Carton, X., Morel, Y. & Serpette, A. 2002 Dynamics and evolution of a northern meddy. J. Phys. Oceanogr. 32, 55–79.Google Scholar
Päschke, E., Marschalik, P., Owinoh, A. Z. & Klein, R. 2012 Motion and structure of atmospheric mesoscale baroclinic vortices: dry air and weak environmental shear. J. Fluid Mech. 701, 137–170.Google Scholar
Reinaud, J. N. 2017 Piecewise uniform potential vorticity pancake shielded vortices. Geophys. Astrophys. Fluid Dyn. 111 (1), 32–64.Google Scholar
Richardson, P. L., Bower, A. S. & Zenk, W. 2000 A census of meddies tracked by floats. Prog. Oceanogr. 45, 209–250.Google Scholar
Tsang, Y.-K. & Dritschel, D. G. 2014 Ellipsoidal vortices in rotating stratified fluids: beyond the quasi-geostrophic approximation. J. Fluid Mech. 762, 196–231.Google Scholar
Tung, K. K. 1983 Initial-value problems for Rossby waves in a shear flow with critical level. J. Fluid Mech. 133, 443–469.Google Scholar
Viúdez, A. 2007 The origin of the stationary frontal wave packet spontaneously generated in rotating stratified vortex dipoles. J. Fluid Mech. 593, 359–383.Google Scholar
Viúdez, A. & Dritschel, D. G. 2003 Vertical velocity in mesoscale geophysical flows. J. Fluid Mech. 483, 199–223.Google Scholar
Yim, E., Billant, P. & Ménesguen, C. 2016 Stability of an isolated pancake vortex in continuously stratified-rotating fluids. J. Fluid Mech. 801, 508–553.Google Scholar

Viúdez et al. supplementary movie 1

Time evolution of potential vorticity anomaly isosurfaces PVA=-0.2 (blue) and PVA=0.14 (grey). PVA contours at z=0, from PVA=0.01 to PVA=0.18, are included. The colour distribution corresponds to PVA at z=0.

Download Viúdez et al. supplementary movie 1(Video)
Video 75.1 MB

Viúdez et al. supplementary movie 2

Time evolution of vertical velocity isosurfaces w=-0.001 (blue) and w=0.001 (red). The black contours and colour distribution corresponds to the PVA. The white lines join the vertical velocity centres at every depth.

Download Viúdez et al. supplementary movie 2(Video)
Video 5.6 MB