Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-05T02:04:02.521Z Has data issue: false hasContentIssue false
  • English
  • Français

Interaction between near-wall streaks and large-scale motions in turbulent channel flows

Published online by Cambridge University Press:  08 April 2022

Zisong Zhou Open the ORCID record for Zisong Zhou [Opens in a new window] ,
Chun-Xiao Xu Open the ORCID record for Chun-Xiao Xu [Opens in a new window]  and
Javier Jiménez Open the ORCID record for Javier Jiménez [Opens in a new window]
Zisong Zhou
Affiliation:
AML, Department of Engineering Mechanics, Tsinghua University, Beijing 100084, PR China
Chun-Xiao Xu*
Affiliation:
AML, Department of Engineering Mechanics, Tsinghua University, Beijing 100084, PR China
Javier Jiménez
Affiliation:
School of Aeronautics, Universidad Politécnica de Madrid, 28040 Madrid, Spain
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

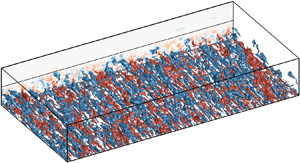
The interactions between the near-wall streaks and the large-scale motions (LSMs) of the outer region of wall-bounded turbulent flows are investigated. The co-supporting hypothesis of Toh & Itano (J. Fluid Mech., vol. 524, 2005, pp. 249–262) is checked in full-scale channels at low to moderate Reynolds numbers, from two points of view. To study the top-down influence of the outer structures on the spanwise motion of the near-wall streaks, a method inspired by particle-image velocimetry is used to track the spanwise position of the streaks. Their spanwise advection velocity is found to be affected by the hierarchy of large-scale circulations in the logarithmic layer, but their spanwise streak density is only weakly related to the LSMs. The evidence suggests that a top-down influence exists and drives the drift of the streaks in the spanwise direction, as suggested by Toh & Itano (J. Fluid Mech., vol. 524, 2005, pp. 249–262), but that the hypothesised streak accumulation rarely occurs. Numerical experiments at $Re_{\tau }\thickapprox 535$ are then performed to clarify the role of the near-wall streaks in the generation and preservation of the outer LSMs. The results show that the merger of the near-wall streaks is only weakly correlated with the generation of the LSMs, and that removing the near-wall roots of the LSMs does not affect the evolution of their outer region. It is concluded that the bottom-up influence from the near-wall streaks is not essential for the LSM generation and preservation, also weakening the evidence for the co-supporting hypothesis.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulence simulation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 940 , 10 June 2022 , A23
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abe, H., Antonia, R. & Toh, S. 2018 Large-scale structures in a turbulent channel flow with a minimal streamwise flow unit. J. Fluid Mech. 850, 733–768.CrossRefGoogle Scholar
Abe, H., Kawamura, H. & Choi, H. 2004 Very large-scale structures and their effects on the wall shear-stress fluctuations in a turbulent channel flow up to $Re \tau = 640$. Trans. ASME J. Fluids Engng 126 (5), 835–843.CrossRefGoogle Scholar
Adrian, R.J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19 (4), 041301.CrossRefGoogle Scholar
del Álamo, J.C. & Jiménez, J. 2003 Spectra of the very large anisotropic scales in turbulent channels. Phys. Fluids 15 (6), L41–L44.CrossRefGoogle Scholar
del Álamo, J.C. & Jiménez, J. 2006 Linear energy amplification in turbulent channels. J. Fluid Mech. 559, 205–213.CrossRefGoogle Scholar
del Álamo, J.C. & Jiménez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor's approximation. J. Fluid Mech. 640, 5–26.CrossRefGoogle Scholar
del Álamo, J.C., Jiménez, J., Zandonade, P. & Moser, R.D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.CrossRefGoogle Scholar
Balakumar, B.J. & Adrian, R.J. 2007 Large- and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. A 365 (1852), 665–681.CrossRefGoogle ScholarPubMed
Baltzer, J.R., Adrian, R.J. & Wu, X.H. 2013 Structural organization of large and very large scales in turbulent pipe flow simulation. J. Fluid Mech. 720, 236–279.CrossRefGoogle Scholar
Butler, K.M. & Farrell, B.F. 1993 Optimal perturbations and streak spacing in wall-bounded shear flow. Phys. Fluids A 5, 774–777.CrossRefGoogle Scholar
Cossu, C. & Hwang, Y. 2017 Self-sustaining processes at all scales in wall-bounded turbulent shear flows. Phil. Trans. R. Soc. A 375 (2089), 20160088.CrossRefGoogle ScholarPubMed
Deng, B.-Q. & Xu, C.-X. 2012 Influence of active control on STG-based generation of streamwise vortices in near-wall turbulence. J. Fluid Mech. 710, 234–259.CrossRefGoogle Scholar
Dong, S., Lozano-Durán, A., Sekimoto, A. & Jiménez, J. 2017 Coherent structures in statistically stationary homogeneous shear turbulence. J. Fluid Mech. 816, 167–208.CrossRefGoogle Scholar
Doohan, P., Willis, A.P. & Hwang, Y. 2021 Minimal multi-scale dynamics of near-wall turbulence. J. Fluid Mech. 913, A8.CrossRefGoogle Scholar
Flores, O. & Jiménez, J. 2006 Effect of wall-boundary disturbances on turbulent channel flows. J. Fluid Mech. 566, 357–376.CrossRefGoogle Scholar
Flores, O. & Jiménez, J. 2010 Hierarchy of minimal flow units in the logarithmic layer. Phys. Fluids 22 (7), 071704.CrossRefGoogle Scholar
Guala, M., Hommema, S.E. & Adrian, R.J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.CrossRefGoogle Scholar
Hamilton, J., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.CrossRefGoogle Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to $Re_\tau =2003$. Phys. Fluids 18, 011702.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007 a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007 b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. A 365 (1852), 647–664.CrossRefGoogle ScholarPubMed
Hwang, Y. & Cossu, C. 2010 Self-sustained process at large scales in turbulent channel flow. Phys. Rev. Lett. 105 (4), 044505.CrossRefGoogle ScholarPubMed
Jiménez, J. 1998 The largest scales of turbulence. In CTR Ann. Res. Briefs (ed. P. Moin, W.C. Reynolds & N.N. Mansour), pp. 137–154. Stanford University.Google Scholar
Jiménez, J. 2012 Cascades in wall-bounded turbulence. Annu. Rev. Fluid Mech. 44, 27–45.CrossRefGoogle Scholar
Jiménez, J., Kawahara, G., Simens, M.P., Nagata, M. & Shiba, M. 2005 Characterization of near-wall turbulence in terms of equilibrium and ‘bursting’ solutions. Phys. Fluids 17, 015105.CrossRefGoogle Scholar
Jiménez, J. & Moin, P. 1991 The minimal flow unit in near-wall turbulence. J. Fluid Mech. 225, 213–240.CrossRefGoogle Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.CrossRefGoogle Scholar
Kim, J. & Hussain, F. 1993 Propagation velocity of perturbations in channel flow. Phys. Fluids A 5, 695–706.CrossRefGoogle Scholar
Kim, K.C. & Adrian, R.J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417–422.CrossRefGoogle Scholar
Kline, S.J., Reynolds, W.C., Schraub, F.A. & Runstadler, P.W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30 (4), 741–773.CrossRefGoogle Scholar
Kwon, Y. & Jiménez, J. 2021 An isolated logarithmic layer. J. Fluid Mech. 916, A35.CrossRefGoogle Scholar
Lee, J.H. & Sung, H.J. 2011 Very-large-scale motions in a turbulent boundary layer. J. Fluid Mech. 673, 80–120.CrossRefGoogle Scholar
Lozano-Durán, A. & Jiménez, J. 2014 a Effect of the computational domain on direct simulations of turbulent channels up to $Re_\tau = 4200$. Phys. Fluids 26 (1), 011702.CrossRefGoogle Scholar
Lozano-Durán, A. & Jiménez, J. 2014 b Time-resolved evolution of coherent structures in turbulent channels: characterization of eddies and cascades. J. Fluid Mech. 759, 432–471.CrossRefGoogle Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010 a High Reynolds number effects in wall turbulence. Intl J. Heat Fluid Flow 31 (3), 418–428.CrossRefGoogle Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010 b Predictive model for wall-bounded turbulent flow. Science 329 (5988), 193–196.CrossRefGoogle ScholarPubMed
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.CrossRefGoogle Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2011 A predictive inner–outer model for streamwise turbulence statistics in wall-bounded flows. J. Fluid Mech. 681, 537–566.CrossRefGoogle Scholar
McKeon, B. & Sharma, A. 2010 A critical-layer framework for turbulent pipe flow. J. Fluid Mech. 658, 336–382.CrossRefGoogle Scholar
Mizuno, Y. & Jiménez, J. 2013 Wall turbulence without walls. J. Fluid Mech. 723, 429–455.CrossRefGoogle Scholar
Monty, J.P., Hutchins, N., Ng, H.C.H., Marusic, I. & Chong, M.S. 2009 A comparison of turbulent pipe, channel and boundary layer flows. J. Fluid Mech. 632, 431–442.CrossRefGoogle Scholar
Pujals, G., García-Villalba, M., Cossu, C. & Depardon, S. 2009 A note on optimal transient growth in turbulent channel flows. Phys. Fluids 21 (1), 015109.CrossRefGoogle Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.CrossRefGoogle Scholar
Scovazzi, G., Jiménez, J. & Moin, P. 2001 LES of the very large scales in a $Re_\tau =920$ channel. In Proc. Div. Fluid Dyn. (ed. P. Moin), pp. KF–5. American Physical Society.Google Scholar
Smith, C.R. & Metzler, S.P. 1983 The characteristics of low speed streaks in the near wall region of a turbulent boundary layer. J. Fluid Mech. 129, 27–54.CrossRefGoogle Scholar
Tanahashi, M., Kang, S.-J., Miyamoto, T., Shiokawa, S. & Miyauchi, T. 2004 Scaling law of fine scale eddies in turbulent channel flow at to $Re_\tau =800$. Intl J. Heat Fluid Flow 25, 331–340.CrossRefGoogle Scholar
Toh, S. & Itano, T. 2005 Interaction between a large-scale structure and near-wall structures in channel flow. J. Fluid Mech. 524, 249–262.CrossRefGoogle Scholar
Townsend, A.A. 1961 Equilibrium layers and wall turbulence. J. Fluid Mech. 11 (1), 97–120.CrossRefGoogle Scholar
Townsend, A.A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Tuerke, F. & Jiménez, J. 2013 Simulations of turbulent channels with prescribed velocity profiles. J. Fluid Mech. 723, 587–603.CrossRefGoogle Scholar
Zhang, C. & Chernyshenko, S.I. 2016 Quasisteady quasihomogeneous description of the scale interactions in near-wall turbulence. Phys. Rev. Fluids 1, 014401.CrossRefGoogle Scholar