Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-26T19:41:04.372Z Has data issue: false hasContentIssue false
  • English
  • Français

Interaction between breaking-induced vortices and near-bed structures. Part 1. Experimental and theoretical investigation

Published online by Cambridge University Press:  19 April 2022

Maurizio Brocchini Open the ORCID record for Maurizio Brocchini [Opens in a new window] ,
Francesco Marini Open the ORCID record for Francesco Marini [Opens in a new window] ,
Matteo Postacchini Open the ORCID record for Matteo Postacchini [Opens in a new window] ,
Gianluca Zitti Open the ORCID record for Gianluca Zitti [Opens in a new window] ,
Massimo Falchi Open the ORCID record for Massimo Falchi [Opens in a new window]  and
Zhihua Xie Open the ORCID record for Zhihua Xie [Opens in a new window]
Maurizio Brocchini
Affiliation:
Department of Civil and Building Engineering, and Architecture, Università Politecnica delle Marche, 60131, Ancona, Italy
Francesco Marini
Affiliation:
Department of Civil and Building Engineering, and Architecture, Università Politecnica delle Marche, 60131, Ancona, Italy
Matteo Postacchini
Affiliation:
Department of Civil and Building Engineering, and Architecture, Università Politecnica delle Marche, 60131, Ancona, Italy
Gianluca Zitti*
Affiliation:
Department of Civil and Building Engineering, and Architecture, Università Politecnica delle Marche, 60131, Ancona, Italy
Massimo Falchi
Affiliation:
National Research Council, CNR-INM, 00128, Rome, Italy
Zhihua Xie
Affiliation:
School of Engineering, Cardiff University, Cardiff, CF24 3AA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

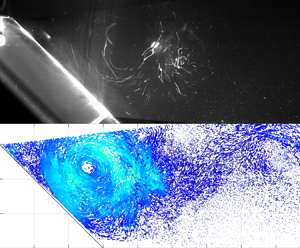
The present work describes the vortex–vortex interactions observed during laboratory experiments, where a single regular water wave is allowed to travel over a discontinuous rigid bed promoting the generation of both near-bed and surface vortices. While near-bed vortices are generated by the flow separation occurring at the bed discontinuity, surface vortices are induced by the wave breaking in conjunction with a breaking-induced jet. A ‘backward breaking’ (previously observed in the case of solitary waves) occurs at the air–water interface downstream of the discontinuity and generates a surface anticlockwise vortex that interacts with the near-bed clockwise vortex. With the vortex–vortex interaction influenced by many physical mechanisms, a point-vortex model, by which vortices evolve under both self-advection (in relation to both free surface and seabed) and mutual interaction, has been implemented to separately investigate the vortex- and wave-induced dynamics. The available data indicate that both self-advection and mutual interaction are the governing mechanisms for the downward motion of the surface vortex, with the effect of the breaking-induced jet being negligible. The same two mechanisms, combined with the mean flow, are responsible for the almost horizontal and oscillating path of the near-bed vortex. The investigation of the vortex paths allow us to group the performed tests into three distinct classes, each characterized by a specific range of wave nonlinearity. The time evolution of the main variables characterizing the vortices (e.g. circulation, kinetic energy, enstrophy, radius) and their maximum values increase with the wave nonlinearity, such dependences being described by synthetic best-fit formulas.

JFM classification

Vortex Flows: Vortex interactions Vortex Flows: Vortex dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 940 , 10 June 2022 , A44
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Batchelor, G.K. 1971 Small-scale variation of convected quantities like temperature in turbulent fluid. Part 1. General discussion and the case of small conductivity. J. Fluid Mech. 5, 113–133.CrossRefGoogle Scholar
Best, J. 2005 The fluid dynamics of river dunes: a review and some future research directions. J. Geophys. Res. 110, F4S02.Google Scholar
Bourgoin, A., Guillou, S.S., Thiébot, J. & Ata, R. 2021 Use of large-eddy simulation for the bed shear stress estimation over a dune. Intl J. Sedim. Res. 36 (6), 687–695.CrossRefGoogle Scholar
Bristow, N.R., Blois, G., Best, J.L. & Christensen, K.T. 2020 Secondary flows and vortex structure associated with isolated and interacting barchan dunes. J. Geophys. Res. 125 (2), e2019JF005257.Google Scholar
Brocchini, M., Kennedy, A., Soldini, L. & Mancinelli, A. 2004 Topographically controlled, breaking-wave-induced macrovortices. Part 1. Widely separated breakwaters. J. Fluid Mech. 507, 289–307.CrossRefGoogle Scholar
Bühler, O. & Jacobson, T.E. 2001 Wave-driven currents and vortex dynamics on barred beaches. J. Fluid Mech. 449, 313–339.CrossRefGoogle Scholar
Chang, K.A., Hsu, T.J. & Liu, P.L.F. 2001 Vortex generation and evolution in water waves propagating over a submerged rectangular obstacle: part I. Solitary waves. Coastal Engng 44 (1), 13–36.CrossRefGoogle Scholar
Chang, K.A., Hsu, T.J. & Liu, P.L.F. 2005 Vortex generation and evolution in water waves propagating over a submerged rectangular obstacle: part II: Cnoidal waves. Coastal Engng 52 (3), 257–283.CrossRefGoogle Scholar
Cheng, M., Lou, J. & Luo, L.S. 2010 Numerical study of a vortex ring impacting a flat wall. J. Fluid Mech. 660, 430–455.CrossRefGoogle Scholar
Chickadel, C.C., Horner-Devine, A.R., Talke, S.A. & Jessup, A.T. 2009 Vertical boil propagation from a submerged estuarine sill. Geophys. Res. Lett. 36, L10601.CrossRefGoogle Scholar
Cooker, M., Peregrine, D.H., Vidal, C. & Dold, J.W. 1990 The interaction between a solitary wave and a submerged semicircular cylinder. J. Fluid Mech. 215, 1–22.CrossRefGoogle Scholar
Corvaro, S., Marini, F., Mancinelli, A., Lorenzoni, C. & Brocchini, M. 2018 Hydro-and morpho-dynamics induced by a vertical slender pile under regular and random waves. ASCE J. Waterway Port Coastal Ocean Engng 144 (6), 04018018.CrossRefGoogle Scholar
Crow, S.C. 1970 Stability theory for a pair of trailing vortices. AIAA J. 8 (12), 2172–2179.CrossRefGoogle Scholar
Curtis, C.W. & Kalisch, H. 2017 Vortex dynamics in nonlinear free surface flows. Phys. Fluids 29 (3), 032101.CrossRefGoogle Scholar
Fabre, D., Jacquin, L. & Loof, A. 2002 Optimal perturbations in a four-vortex aircraft wake in counter-rotating configuration. J. Fluid Mech. 451, 319–328.CrossRefGoogle Scholar
Falchi, M. & Romano, G.P. 2009 Evaluation of the performance of high-speed PIV compared to standard PIV in a turbulent jet. Exp. Fluids 47 (3), 509–526.CrossRefGoogle Scholar
Gharib, M., Rambod, E. & Shariff, K. 1998 A universal time scale for vortex ring formation. J. Fluid Mech. 360, 121–140.CrossRefGoogle Scholar
Grilli, S.T., Losada, M.A. & Martin, F. 1994 Characteristics of solitary wave breaking induced by breakwaters. ASCE J. Waterway Port Coastal Ocean Engng 120 (1), 74–92.CrossRefGoogle Scholar
Janke, T., Schwarze, R. & Bauer, K. 2020 Part2track: a matlab package for double frame and time resolved particle tracking velocimetry. SoftwareX 11, 100413.CrossRefGoogle Scholar
Kennedy, A.B., Brocchini, M., Soldini, L. & Gutierrez, E. 2006 Topographically controlled, breaking-wave-induced macrovortices. Part 2. Changing geometries. J. Fluid Mech. 559, 57–80.CrossRefGoogle Scholar
Kuvshinov, B.N. & Schep, T.J. 2016 Point-vortex approach in two-dimensional turbulence. Plasma Phys. Rep. 42 (5), 523–536.CrossRefGoogle Scholar
Leweke, T., Le Dizes, S. & Williamson, C.H.K. 2016 Dynamics and instabilities of vortex pairs. Annu. Rev. Fluid Mech. 48, 507–541.CrossRefGoogle Scholar
Leweke, T. & Williamson, C.H.K. 1998 Cooperative elliptic instability of a vortex pair. J. Fluid Mech. 360, 85–119.CrossRefGoogle Scholar
Li, C.Y., Shih, R.S., Weng, W.K. & Liao, T.W. 2021 Analysis of vortex formation and energy dissipation during interaction of solitary-like waves with submerged breakwaters based on particle image velocimetry. Appl. Ocean Res. 110, 102579.CrossRefGoogle Scholar
Lorenzoni, C., Postacchini, M., Brocchini, M. & Mancinelli, A. 2016 Experimental study of the short-term efficiency of different breakwater configurations on beach protection. J. Ocean Engng Mar. Energy 2 (2), 195–210.CrossRefGoogle Scholar
Lorenzoni, C., Soldini, L., Brocchini, M., Mancinelli, A., Postacchini, M., Seta, E. & Corvaro, S. 2010 Working of defense coastal structures dissipating by macroroughness. ASCE J. Waterway Port Coastal Ocean Engng 136 (2), 79–90.CrossRefGoogle Scholar
Madsen, P.A., Fuhrman, D.R. & Schäffer, H.A. 2008 On the solitary wave paradigm for tsunamis. J. Geophys. Res. 113, C12012.Google Scholar
Meunier, P., Le Dizes, S. & Leweke, T. 2005 Physics of vortex merging. C. R. Phys. 6 (4–5), 431–450.CrossRefGoogle Scholar
Miozzi, M., Postacchini, M., Corvaro, S. & Brocchini, M. 2015 Whole-wavelength description of a wave boundary layer over permeable wall. Exp. Fluids 56 (6), 127.CrossRefGoogle Scholar
Nadaoka, K., Hino, M. & Koyano, Y. 1989 Structure of the turbulent flow field under breaking waves in the surf zone. J. Fluid Mech. 204, 359–387.CrossRefGoogle Scholar
Ryan, K., Butler, C.J. & Sheard, G.J. 2012 Stability characteristics of a counter-rotating unequal-strength batchelor vortex pair. J. Fluid Mech. 696, 374–401.CrossRefGoogle Scholar
Sinha, S., Hardy, R.J., Blois, G., Best, J.L. & Sambrook Smith, G.H. 2017 A numerical investigation into the importance of bed permeability on determining flow structures over river dunes. Water Resour. Res. 53 (4), 3067–3086.CrossRefGoogle Scholar
So, J., Ryan, K. & Sheard, G.J. 2011 Short-wave instabilities on a vortex pair of unequal strength circulation ratio. Appl. Math. Model. 35 (4), 1581–1590.CrossRefGoogle Scholar
Terrile, E. & Brocchini, M. 2007 A dissipative point-vortex model for nearshore circulation. J. Fluid Mech. 589, 455–478.CrossRefGoogle Scholar
Wu, Y.T., Hsiao, S.C., Huang, Z.C. & Hwang, K.S. 2012 Propagation of solitary waves over a bottom-mounted barrier. Coastal Engng 62, 31–47.CrossRefGoogle Scholar
Zheng, Y., Dong, L. & Rinoshika, A. 2019 Multi-scale wake structures around the dune. Expl Therm. Fluid Sci. 104, 209–220.CrossRefGoogle Scholar
Supplementary material: File

Brocchini et al. supplementary material

Brocchini et al. supplementary material

Download Brocchini et al. supplementary material(File)
File 3.4 MB