Published online by Cambridge University Press: 19 December 2018
Langmuir circulations (LCs) generated by the interaction between wind-driven currents and surface waves can engulf the whole water column in neutrally stratified shallow water and interact with the turbulence in the bottom boundary layer. In this study, we perform a mechanistic study using wall-resolved large-eddy simulations (LES) based on the Craik–Leibovich equations to investigate the effects of LCs on turbulence statistics in the bottom half of shallow water. The highest Reynolds number considered in this paper, 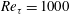 $Re_{\unicode[STIX]{x1D70F}}=1000$, is larger than the values considered in wall-resolved LES studies of shallow-water Langmuir turbulence reported in literature. The logarithmic layer is diagnosed based on a plateau region in the profile of a diagnostic function. It is found that the logarithmic layer disrupted at
$Re_{\unicode[STIX]{x1D70F}}=1000$, is larger than the values considered in wall-resolved LES studies of shallow-water Langmuir turbulence reported in literature. The logarithmic layer is diagnosed based on a plateau region in the profile of a diagnostic function. It is found that the logarithmic layer disrupted at 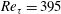 $Re_{\unicode[STIX]{x1D70F}}=395$ reappears at
$Re_{\unicode[STIX]{x1D70F}}=395$ reappears at 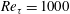 $Re_{\unicode[STIX]{x1D70F}}=1000$, but the von Kármán constant is slightly different from the traditional value
$Re_{\unicode[STIX]{x1D70F}}=1000$, but the von Kármán constant is slightly different from the traditional value 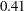 $0.41$. To study the effects of LCs on turbulence statistics, LCs are extracted using streamwise averaging. The velocity fluctuations
$0.41$. To study the effects of LCs on turbulence statistics, LCs are extracted using streamwise averaging. The velocity fluctuations 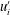 $u_{i}^{\prime }$ are decomposed into a LC-coherent part
$u_{i}^{\prime }$ are decomposed into a LC-coherent part 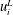 $u_{i}^{L}$ and a residual turbulence part
$u_{i}^{L}$ and a residual turbulence part 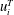 $u_{i}^{T}$. It is found that the profiles of LC-coherent Reynolds shear stress
$u_{i}^{T}$. It is found that the profiles of LC-coherent Reynolds shear stress 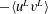 $-\langle u^{L}v^{L}\rangle$ obtained at various Reynolds numbers are close to each other in the water-column coordinate
$-\langle u^{L}v^{L}\rangle$ obtained at various Reynolds numbers are close to each other in the water-column coordinate 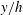 $y/h$, with
$y/h$, with 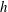 $h$ being the half-water depth. As the Reynolds number (or, by definition, the ratio between the outer and inner length scales) increases, the influence of LCs on the near-bottom momentum transfer is reduced, which is responsible for the reappearance of the logarithmic layer. At all of the Reynolds numbers under investigation, the peaks of
$h$ being the half-water depth. As the Reynolds number (or, by definition, the ratio between the outer and inner length scales) increases, the influence of LCs on the near-bottom momentum transfer is reduced, which is responsible for the reappearance of the logarithmic layer. At all of the Reynolds numbers under investigation, the peaks of 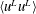 $\langle u^{L}u^{L}\rangle$ are collocated in the water-column coordinate
$\langle u^{L}u^{L}\rangle$ are collocated in the water-column coordinate 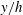 $y/h$, while those of
$y/h$, while those of 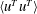 $\langle u^{T}u^{T}\rangle$ are collocated in the inner-scale coordinate
$\langle u^{T}u^{T}\rangle$ are collocated in the inner-scale coordinate 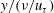 $y/(\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}})$. Due to the increase in the distance between the peaks of
$y/(\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}})$. Due to the increase in the distance between the peaks of 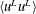 $\langle u^{L}u^{L}\rangle$ and
$\langle u^{L}u^{L}\rangle$ and 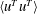 $\langle u^{T}u^{T}\rangle$ with the Reynolds number, the profile of
$\langle u^{T}u^{T}\rangle$ with the Reynolds number, the profile of  $\langle u^{\prime }u^{\prime }\rangle$ forms a bimodal shape at
$\langle u^{\prime }u^{\prime }\rangle$ forms a bimodal shape at 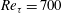 $Re_{\unicode[STIX]{x1D70F}}=700$ and
$Re_{\unicode[STIX]{x1D70F}}=700$ and 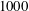 $1000$.
$1000$.