3.1. Evolution of the turbulent mixing layer

For all of the simulations listed in table 1, we take non-dimensional time $t=0$ to correspond to the time of billow saturation, or maximal $\mathcal {K}_{2\text{-}D}$, as described above. To get an overview of flow behaviour, figure 1 shows successive 2-D contour plots through $y=0$ of the spanwise vorticity field $\omega _y =\partial _z u - \partial _x w$, demonstrating the turbulent transition behaviour for flows L10 and T16. The presence of the ambient stratification in the L10 flow means that a considerably lower ${Ri}_0=0.10$ produces a billow of similar height to its T16 counterpart with ${Ri}_0=0.16$. As is to be expected at ${Re}=6000$ following the investigations of Mashayek & Peltier (Reference Mashayek and Peltier2012a,Reference Mashayek and Peltierb), the noise perturbation at $t=0$ triggers a variety of rapidly emerging secondary instabilities that facilitate the breakdown to turbulence, which then becomes increasingly isotropic within the mixing layer as it evolves. Analogous behaviour is observed for the simulations L13 and T19. The main qualitative difference between the class L and T simulations is the presence of faint internal gravity waves in the L simulations that propagate away from the turbulent layer in class L simulations through the turbulent/non-turbulent layer interface (TNTI), which is visible most distinctly at the turbulent layer boundary in figure 1(d). (The dynamics of the TNTI are discussed in detail in Watanabe et al. Reference Watanabe, Riley, Nagata, Onishi and Matsuda2018.) We note here that the relatively weak far field stratification in both L simulations means that the total energy propagated away from the shear layer by gravity waves during the mixing process is small compared with the initial kinetic energy (${<}1\,\%$) and far field turbulent fluctuations are insignificant in magnitude compared to within the turbulent region, at least whilst more intense turbulence persists. This is the period during which the majority of irreversible mixing takes place; hence, for the present study, we will not be largely concerned with internal wave effects and will instead focus primarily on the dynamics within the turbulent layer. Stronger far field stratifications may result in larger amounts of energy extraction from the turbulent region. For example, Pham et al. (Reference Pham, Sarkar and Brucker2009) show that when the shear layer lies above a region of stronger stratification with $N^2 = -{Ri}_0\partial \bar {\rho }/\partial z \geq 0.25$, the amount of turbulent energy transported into the far field by internal waves can be up to 15 % of the initial mean kinetic energy inside the shear layer. Such a set-up might be more appropriate to model, for example, a turbulent shear layer in the ocean thermocline, as opposed to more weakly stratified abyssal waters.

Figure 1. Spanwise slices through $y=0$ for various indicated times during the turbulent transition phase of flow showing contours of spanwise vorticity for simulations (a–d) L10 and (e–h) T16.

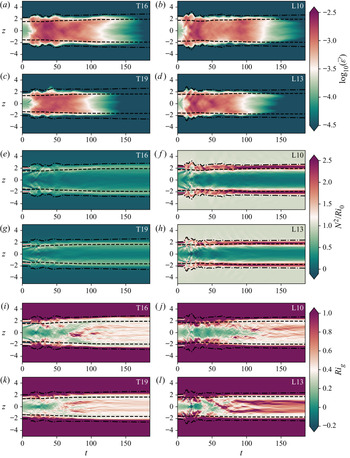
To investigate further the similarities and differences between the mixing layers produced by KHI in the L and T simulations, we examine the evolution of the horizontally averaged turbulent dissipation $\bar {\varepsilon '}(z,t) \equiv \overline {\partial _j u'_i\partial _j u'_i}/{Re}$, the normalized buoyancy frequency $N^2(z,t)/{Ri}_0 = -\partial \bar {\rho }/\partial z$ and the local gradient Richardson number ${Ri}_g(z,t)$ defined in (2.8). The results are shown in figure 2, where we also plot the evolution of the height of the turbulent mixing layer as measured in two different ways. Firstly, we plot the momentum thickness

(3.1)\begin{equation} \ell_u(t) = \int_{{-}L_z/2}^{L_z/2} (1-\bar{u}(z,t)^2)\,\textrm{d} z \end{equation}

defined by Smyth & Moum (Reference Smyth and Moum2000) as an estimate for the vertical extent of the mixing layer for simulations that have a background shear profile given by a hyperbolic tangent function (note their definition includes an additional factor of 4 due to differences in the non-dimensionalization). Secondly, similar to VanDine et al. (Reference VanDine, Pham and Sarkar2021), we identify a so-called ‘transition layer’ (TL) as a region of enhanced stratification (specifically, we demarcate the edges of these regions where $|\partial \bar {\rho }/\partial z|$ becomes larger than the far field stratification by more than 10 % of its maximum value) immediately above and below the mixing layer and plot the evolution of the outer boundaries of these layers for each simulation.

Figure 2. Time-evolving vertical profiles of (a–d) horizontally averaged turbulent dissipation $\bar {\varepsilon '} (z,t)$, (e–h) normalized buoyancy frequency $N^2(z,t)/Ri_0$ and (i–l) gradient Richardson number $Ri_g(z,t)$ for each simulation as indicated in the top right-hand corner of the panels. Dashed lines are the contours $z=\pm \ell _u(t)/2$, whilst dot–dashed lines are the contours marking the edges of the transition layers.

Looking at the structural evolution of $\bar {\varepsilon '}$, flows T16 and L10 are qualitatively very similar in terms of the extent of the turbulent mixing layer, the patterns of more intense turbulence within the mixing layer and the time taken for turbulence to decay. Flows T19 and L13 are likewise qualitatively similar. There are slight differences in $\bar {\varepsilon '}$ between L and T simulations during the early part of the flow, with the asymmetry of young turbulence rotating around the distorted laminar billow core (as seen in figure 1c) causing wave-like patterns at the edge of the mixing region in L simulations for $t<40$. More obvious differences between L and T simulations are visible in the evolution of the background stratification $N^2/Ri_0$, which is much larger in the TLs for L simulations than it is for T simulations. The importance of the TL has been investigated in detail by VanDine et al. (Reference VanDine, Pham and Sarkar2021), who argue that the dynamics within this region are important and should be included when computing bulk flow statistics. We will explore this issue further in § 3.2. Finally, looking at the evolution of the local gradient Richardson number ${Ri}_g$, we see that the turbulent breakdown in both L and T simulations is characterised by small local values of ${Ri}_g$ in the centre of the mixing layer. Once the turbulence starts to decay, however, class L flows exhibit a distinct increased frequency of relatively larger values of ${Ri}_g$ between the TLs, despite the fact that the dissipation decays in an apparently similar manner between T and L simulations. We will discuss the importance of ${Ri}_g$ for parameterizing mixing in § 3.4.

In general, the observed similarities between corresponding L and T simulations are supported by the behaviour of $\ell _u(t)$ and the boundaries of the TLs, which are both reasonable measures of the height of the mixing layer when turbulence is present. Based on the qualitative similarities between these two pairs of flows that have a similar mixing layer height, it is natural to ask whether the mixing taking place is also quantitatively similar, and whether the behaviour is generic enough such that attempts to parameterize its efficiency do not largely depend on the background stratification.

3.2. Local and global measures of mixing

In order to define mixing appropriately as an irreversible diffusive flux across isopycnals, it is important to distinguish between diabatic processes (those in which the physical properties of individual fluid parcels are modified) associated with mixing and adiabatic processes (those which modify only the distribution of parcels) associated with stirring in the flow. Proceeding as in Caulfield & Peltier (Reference Caulfield and Peltier2000), we divide the total potential energy $\mathscr {P} = {Ri}_0 \langle \rho z \rangle$ into two parts, the background potential energy (BPE) $\mathscr {P}_B$ defined as

(3.2)\begin{equation} \mathscr{P}_B = {Ri}_0 \langle z \rho_B(z) \rangle, \end{equation}

and the available potential energy (APE) $\mathscr {P}_A$ defined in the equation

(3.3)\begin{equation} \mathscr{P} = \mathscr{P}_B + \mathscr{P}_A. \end{equation}

The background density profile $\rho _B(z)$ is obtained by adiabatically rearranging the density field into a gravitationally stable monotonic configuration. An important result obtained by Winters et al. (Reference Winters, Lombard, Riley and D'Asoro1995) states that, for an initially statically stable closed system, the potential energy of this configuration (i.e. the BPE) necessarily increases monotonically with time at a rate bounded below by the rate of diffusion of the mean laminar flow $\mathscr {D}_p = \int _{-L_z/2}^{L_z/2} z(\partial ^2\bar {\rho }/\partial z^2)\,\textrm {d} z$. Thus, by taking the time derivative of (3.3) we can write

(3.4a,b)\begin{equation} \frac{{\rm d}\mathscr{P}_B}{{\rm d}t} = \mathscr{M} + \mathscr{D}_p,\quad \frac{{\rm d}\mathscr{P}_A}{{\rm d}t} ={-}\mathscr{B} - \mathscr{M}, \end{equation}

where $\mathscr {B}\equiv -{Ri}_0 \langle \rho w \rangle$ is the volume integrated buoyancy flux and $\mathscr {M}$ is the strictly non-negative mixing rate that occurs due to macroscopic fluid motions. Note that we have $\mathscr {D}_p = 2{Ri}_0/({Re}{Pr} L_z)$ for T simulations and $\mathscr {D}_p=0$ for L simulations. From this definition of mixing, it is clear that BPE effectively increases ultimately due to conversion of energy from the APE reservoir. We compute $\mathscr {M}$ by taking a numerical time derivative of $\mathscr {P}_B$, which is evaluated at each time step using an approximation for $\rho _B(z)$ calculated using the probability density function of the full 3-D density field as described in Tseng & Ferziger (Reference Tseng and Ferziger2001).

The mixing rate $\mathscr {M}$ is global by construction, and relies on the assumption that there is no flux of energy into or out of the domain. Whilst appropriate for our class T simulations in which energy is confined to the mixing layer by the lack of ambient stratification, possible issues arise in class L simulations where internal waves generated by turbulence cause fluctuations in the mixing rate $\mathscr {M}$ which become significant at later times when the turbulence is decaying. In order to isolate the mixing due to turbulence, it is more appropriate to invoke an alternative definition of mixing that can be applied to local regions. We appeal to a local definition of APE originally formulated by Holliday & Mcintyre (Reference Holliday and Mcintyre1981) and Andrews (Reference Andrews1981), which has seen recent interest applied to numerical simulations of turbulence in domains where boundary fluxes and large-scale internal waves complicate global definitions of mixing (Howland, Taylor & Caulfield Reference Howland, Taylor and Caulfield2021). Following Scotti & White (Reference Scotti and White2014), we define local APE density $E_{APE}$ as

(3.5)\begin{equation} E_{APE}(x,y,z,t)\equiv {Ri}_0 \int_{\rho_B(z,t)}^{\rho(x,y,z,t)} z-z_B(s,t)\,\textrm{d} s, \end{equation}

where $z_B(\rho , t)$ is the reference height of the background density profile $\rho _B$ defined above, such that $z_B(\rho _B(z,t),t) = z$. This is equivalent to the work done in bringing a fluid parcel from its position in the sorted density profile to its actual position in the density field. Volume averaging the above, we recover the global definition $\mathscr {P}_A = {Ri}_0 \langle \rho (z-z_B) \rangle$, which may also be obtained from (3.2) and (3.3). To make progress in defining a local rate of mixing – that is, the rate of conversion from APE into BPE – first note that if we decompose the density field into the background profile $\rho _B$ plus a small perturbation $\delta \rho$, then to leading order we have $E_{APE}\sim {Ri}_0(\partial \rho _B/\partial z)^{-1} \delta \rho ^2/2$. If we assume that this decomposition is approximately equivalent to the turbulent flow decomposition achieved by horizontally averaging, i.e.

(3.6)\begin{equation} \rho(x,y,z,t) = \rho_B(z,t) + \delta\rho(x,y,z,t) \approx \bar{\rho}(z,t)+\rho'(x,y,z,t), \end{equation}

and make the additional strong assumption that the turbulent fluctuations are in fact small perturbations from a uniform imposed buoyancy gradient, then integrating over the turbulent region we obtain the following approximate expression $\tilde {\mathscr {P}}_A$ for APE:

(3.7)\begin{equation} \tilde{\mathscr{P}}_A \equiv \frac{{Ri}_0}{2} \frac{\langle \rho'^2\rangle_T}{\langle \partial \bar{\rho}/\partial z \rangle_T }. \end{equation}

Here the angle brackets $\langle \cdot \rangle _T$ denote a volume average taken over the extent of the mixing layer. The right-hand side can be recognised as an (appropriately scaled) definition of the variance of the density (or, equivalently, the buoyancy) relative to the horizontally averaged density (or buoyancy) distribution.

Assuming the denominator varies slowly in time compared with the numerator, the time evolution of (the approximation) $\tilde {\mathscr {P}}_A$ is given by

(3.8a,b)\begin{equation} \frac{{\rm d}\tilde{\mathscr{P}}_A}{{\rm d}t} = {Ri}_0\langle \rho' w'\rangle_T - \chi,\quad \chi\equiv\frac{{Ri}_0}{{Re} {Pr}} \frac{\langle \partial_i\rho'\partial_i\rho' \rangle_T}{\langle \partial \bar{\rho}/\partial z \rangle_T}, \end{equation}

where $\chi$ is the appropriately normalised positive definite rate of density variance dissipation, often used as an alternative definition for mixing. One advantage of (3.8a,b) is that the numerator and denominator of $\chi$ can be defined pointwise, thus giving rise to a local definition of mixing. There is some degree of ambiguity as to how such pointwise measures should be interpreted. Based on the decomposition in (3.6), we consider two natural local interpretations of (3.8a,b), given by

(3.9)$$\begin{gather} \chi_{{loc}}(x,y,z,t) \equiv \frac{{Ri}_0}{{Re} {Pr}} \frac{{\partial_i\rho'\partial_i\rho'}}{ \langle \partial \bar{\rho}/\partial z \rangle_T}, \end{gather}$$

(3.10)$$\begin{gather}\tilde{\chi}_{{loc}}(x,y,z,t) \equiv \frac{{Ri}_0}{{Re} {Pr}}\frac{{\partial_i\rho'\partial_i\rho'}}{ \partial \widetilde{\bar{\rho}}/\partial z }, \end{gather}$$

where $\widetilde {\bar {\rho }}(z,t)$ represents the horizontally averaged density field which has been sorted to be statically stable to avoid negative local gradients. The horizontal average $\overline {\tilde {\chi }_{{loc}}}$ is analogous to the alternative definition of local mixing used by Arthur et al. (Reference Arthur, Venayagamoorthy, Koseff and Fringer2017), who average in the spanwise direction only in their turbulent decomposition, as opposed to both horizontal directions. Note that the denominator in (3.10) is defined locally as a function of $z$ and $t$ whereas the denominator in (3.9) is a bulk average. In what follows we will be interested in whether the definitions (3.9)–(3.10) lead to accurate approximations of the globally evaluated irreversible mixing rate $\mathscr {M}$ when averaged over the turbulent layer. We have by definition that $\langle \chi _{{loc}} \rangle _T=\chi$, where $\chi$ is defined in (3.8a,b), and we correspondingly define the volume average

(3.11)\begin{equation} \tilde{\chi} \equiv \langle \tilde{\chi}_{{loc}}\rangle_T. \end{equation}

Howland et al. (Reference Howland, Taylor and Caulfield2021) find that $\chi$, as defined in (3.8a,b), is a reasonable approximation for the mixing rate $\mathscr {M}$ in a variety of forced and unforced turbulent flows with an imposed uniform stratification, though their simulations display much weaker overturning behaviour than the KHI billows we consider here. Using simulations of breaking internal waves on slopes, Arthur et al. (Reference Arthur, Venayagamoorthy, Koseff and Fringer2017) show that the way in which local mixing rates are computed (in terms of how local density gradients are inferred from the denominator in $\chi$) can significantly modify values of the corresponding mixing efficiency. To compare the mixing rates $\mathscr {M}$, $\chi$ and $\tilde {\chi }$, we define three corresponding ‘instantaneous’ mixing efficiencies (i.e. based on mixing rates),

(3.12a–c)\begin{equation} \eta_{\mathscr{M}}(t) \equiv \frac{\mathscr{M}}{\mathscr{M}+\langle \varepsilon \rangle},\quad \eta_{\chi}(t) \equiv \frac{\chi}{\chi+\langle \varepsilon \rangle_T},\quad \eta_{\tilde{\chi}}(t) \equiv \frac{\tilde{\chi}}{\tilde{\chi}+\langle \varepsilon \rangle_T}, \end{equation}

where we note that $\varepsilon (x,y,z,t) = \partial _j u_i \partial _j u_i /{Re}$ is the total kinetic energy dissipation, which is then volume averaged over either the entire domain or over the turbulent region as appropriate. We also define the horizontally averaged local mixing efficiency

(3.13)\begin{equation} \eta_{{loc}}(z,t) \equiv \frac{\overline{\tilde{\chi}_{{loc}}}}{\overline{\tilde{\chi}_{{loc}}} + \bar{\varepsilon}}. \end{equation}

We can investigate the evolution of $\eta _{{loc}}$ by plotting a time-evolving normalised frequency distribution or probability density function (p.d.f.), forming a 2-D histogram. Similar analysis for the evolution of horizontally averaged parameter profiles has been carried out by Salehipour, Peltier & Caulfield (Reference Salehipour, Peltier and Caulfield2018) for class T background density profiles. The time-evolving distribution of values of $\eta _{{loc}}$ is shown in figure 3, with plots of $\eta _{\mathscr {M}}$, $\eta _{\chi }$ and $\eta _{\tilde {\chi }}$ superimposed. The left- and right-hand panels of the figure demonstrate the sensitivity of each measure of mixing to the way in which the extent of the turbulent region is defined, that is, either within $\ell _u/2< \leq z\leq \ell _u/2$ or between the boundaries of the TLs above and below the centreline $z=0$. Note that the initial transient behaviour of $\eta _{\mathscr {M}}$ for the T simulations occurs due to the weighting of the initial noise perturbations in the far field. All of the measures of efficiency defined above exhibit similar behaviour for each of the simulations considered, consisting of an initial highly efficient mixing period during which the primary KHI billow is destroyed, followed by a period of roughly constant efficiency of around 0.2, and finally a period of decay as the flow relaminarises. There are noticeable oscillations in $\eta _{\mathscr {M}}$ for both class L simulations as predicted, caused by the internal gravity waves that are produced by turbulent motions and propagate into the far field. These oscillations become increasingly significant as the turbulence decays and the wave-induced far field fluctuations become similar in magnitude to the turbulent fluctuations in the mixing layer, as is seen particularly in simulation L13 which starts to decay earlier than L10. As discussed above, one of the central problems in using a globally defined mixing rate $\mathscr {M}$ is that it essentially assumes the dominant mixing is confined to within the turbulent layer, with no energy flux in or out of the domain. Whilst appropriate for T simulations in which the lack of ambient stratification prevents an outward energy flux, and at early times in L simulations when high-energy turbulence dominates, in general the mixing rate $\mathscr {M}$ calculated by global sorting of the density field should be treated with caution.

Figure 3. Time-evolving frequency p.d.f. of horizontally averaged local mixing efficiency $\eta _{{loc}}$ for simulations (a–b) T16, (c–d) L10, (e–f ) T19 and (g–h) L13. In the left-hand panels values are sampled within the region $-\ell _u/2 \leq z \leq \ell _u/2$, in the right-hand panels values are sampled within the TL boundaries. Plots of $\eta _{\mathscr {M}}(t)$, $\eta _{\chi }(t)$ and $\eta _{\tilde {\chi }}(t)$ are superimposed, and are calculated by taking the vertical averages $\langle \cdot \rangle _T$ over the corresponding definitions of mixing region. Note by definition the global mixing efficiency $\eta _{\mathscr {M}}$ is the same in the left- and right-hand panels.

Here $\eta _{\chi }$ and $\eta _{\tilde {\chi }}$ are appealing alternative measures of mixing efficiency because they do not rely on a global sorting process and, hence, may be averaged over the turbulent region only, though as can be seen from comparing the left- and right-hand panels in figure 3, these measures may be sensitive to the way in which the extent of the mixing region is defined. In particular, the bulk measure $\eta _\chi$ is lower in L simulations when averaged over the region that includes the TL boundaries, due to the fact that large local values of $\partial \bar {\rho }/\partial z$ in the TL cause the denominator of $\chi$ to increase. This is the opposite result to that reported by VanDine et al. (Reference VanDine, Pham and Sarkar2021), but is entirely due to a difference in the definition of the calculated quantities. In particular, VanDine et al. (Reference VanDine, Pham and Sarkar2021) use a constant value of $\langle \partial \bar {\rho }/\partial z \rangle = 1$ defined by the initial density profile as the denominator in their equivalent expression for $\chi$ instead of the time-evolving bulk average as here. Hence, they found that their corresponding $\eta _{\chi }$ increases when including the TLs in vertical averages.

We also point out that, despite the large local values of $\eta _{{loc}}$ that are seen to be present within the TLs for L and T simulations, neither bulk value $\eta _{\tilde {\chi }}$ nor $\eta _{\chi }$ appear to increase when these regions are included in the definition of the extent of the mixing layer. Overall, figure 3 demonstrates that $\eta _{\chi }$ is a reasonable approximation for $\eta _{\mathscr {M}}$ throughout (when the use of the latter is justified as reasoned above), being most accurate to the precise definition $\eta _{\mathscr {M}}$ when the mixing region is defined using $\ell _u(t)$ from (3.1), though the margins of error can become as large as 0.1 at times. The use of $\tilde {\chi }_{{loc}}$ at early times produces mixing efficiencies $\eta _{\tilde {\chi }}$ that are much higher than $\eta _{\mathscr {M}}$ as the denominator in (3.10) can become very small locally due to the presence of overturnings in the flow. Once turbulence becomes more isotropic, all three measures of mixing follow similar trajectories until the end of the simulation, or until the behaviour of $\eta _{\mathscr {M}}$ becomes strongly affected by internal wave oscillations. Despite the differences between them, the plots of $\eta _{\mathscr {M}}$, $\eta _{\chi }$ and $\eta _{\tilde {\chi }}$ all fall within the distribution of values of $\eta _{{loc}}$ throughout the flow evolution.

To summarise our comparison of the mixing rates $\mathscr {M}$, $\chi$ and $\tilde {\chi }$, figure 3 demonstrates that $\chi$ is a useful diagnostic for analysing mixing, in the sense that the corresponding efficiency reasonably approximates the precise value calculated using the mixing rate $\mathscr {M}$ in flows where this is appropriately defined, even when significant overturnings are present. This is important as $\chi$ is much more straightforward to calculate than $\mathscr {M}$ computationally, and additionally may also be calculated using microstructure measurements in the ocean where there is no way to calculate the exact sorted density profile $\rho _B(z)$. Using $\tilde {\chi }$ instead of $\chi$ produces significant overestimates of the mixing rate when overturnings persist in the flow. However, distributions of local efficiency $\eta _{{loc}}$ obtained using vertical profiles of $\overline {\tilde {\chi }_{{loc}}}$ and $\bar {\varepsilon }$ may provide one way of obtaining reasonable bounds or uncertainty estimates for measures of efficiency obtained by volume averaging. Due to the fact that the best estimates for $\eta _{\mathscr {M}}$ come from using $\eta _{\chi }$ obtained by averaging over the region $-\ell _u/2 \leq z\leq -\ell _u/2$, we will from henceforth use $\ell _u(t)$ as the definition of the extent of the mixing layer.

More generally, figure 3 shows a strong similarity in measurements of mixing efficiency between T and L simulations, especially between simulations T16 and L10, and T19 and L13. Using $\eta _{\chi }$ as a reference measure for comparison based on the discussion above, all simulations have an initial peak around $0.8$ and settle at a constant efficiency of around $0.2$ before decaying. This suggests that mixing is not largely affected by the presence of the ambient stratification. As long as distinct overturnings characterised by an initial period of highly efficient mixing exist in the flow, the subsequent period of mixing that they produce appears to be generic, being both qualitatively and quantitatively similar. We will investigate this observation further in § 3.4 by looking at local distributions of commonly used mixing parameters in the flow.

3.3. Influence of secondary instabilities

Here we apply the concepts of local APE and mixing to the period of flow evolution in which secondary instabilities proliferate on the primary billow braid and facilitate the breakdown to turbulence. Mashayek et al. (Reference Mashayek, Caulfield and Peltier2013) argue that these coherent secondary structures are the primary factor contributing to increased mixing efficiency in conditions that optimise their emergence, which they find to occur at ${Ri}_0=0.16$ for their simulations of class T. To investigate the influence of secondary instabilities on mixing efficiency and further the existing discussion from the literature, we invoke a modified version of the T16 flow that has no additional noise perturbation imposed at $t=0$, referred to as UT16, used in our investigation into the impact of resolution on the emergence of secondary instabilities discussed above in § 2.2 and detailed in the Appendix. This flow has exactly the same initial parameters as T16, but does not exhibit the same proliferation of secondary instabilities due to the absence of the perturbation at $t=0$, allowing us to compare the corresponding mixing efficiencies.

The results in § 3.2 indicate that at early times when large overturnings are present in the flow, $\chi _{{loc}}$ may be a more appropriate choice than $\tilde {\chi }_{{loc}}$ for measuring the local mixing rate as the former gives rise to a bulk mixing efficiency that better approximates the global ‘ground truth’ value $\eta _{\mathscr {M}}$. Figure 4(a) shows the local APE field $E_{APE}(x,y,z,t)$, as defined in (3.5), with superimposed contours of $\chi _{{loc}}$ defined in (3.9) for simulations T16 and UT16 at an equivalent early point in time where secondary instabilities have proliferated on the primary billow in the perturbed T16 simulation. There is a high local APE density in the billow ‘eyelids’ above and below the central core, as well as above and below the billow braid to the right and left of the core for both simulations, indicating these regions are the primary sources of energy for the subsequent mixing. We are interested specifically in where this APE is converted into BPE locally, as measured by the local mixing rate $\chi _{{loc}}$.

Figure 4. (a,b) Spanwise slices through $y=0$ at $t=12$ showing the local APE field $E_{APE}(x,y,z,t)$ with contours of the dissipation of density variance $\chi _{{loc}}$ superimposed for simulations T16 and UT16, as labelled in the top-right corner. (c,d) The same as in (a), instead showing contours of kinetic energy dissipation $\varepsilon$. (e) Time evolution of mixing efficiency $\eta _{\mathscr {M}}$. The vertical dot–dashed line $t=12$ corresponds to the snapshot time from the panels in (a–d).

The main result which can be deduced from the figure is that the action of the secondary instabilities is to deform regions of high local APE density and provide an extended billow braid surface area through which large amounts of local mixing can take place, as is evidenced by the contours of $\chi _{{loc}}$ that are co-located with the edges of regions containing large amounts of local APE. Another important feature of the secondary instabilities is that they dissipate relatively small amounts of kinetic energy before becoming turbulent as is highlighted in figure 4(b), and so they are locally efficient for mixing.

This increased local efficiency is reflected in the global mixing efficiency $\eta _{\mathscr {M}}$ shown in figure 4(c), where it is seen that the mixing efficiency is considerably higher in the T16 flow around the time when secondary instabilities are present. At later times, however, values of $\eta _{\mathscr {M}}$ from both T16 and UT16 settle onto a similar trajectory which suggests that the secondary instabilities do not significantly affect the (instantaneous) mixing efficiency during this later period when they are present. A truly precise measure of local mixing would evaluate the denominator of (3.9) as the gradient of the sorted 3-D density field $\rho _B$ at the density value corresponding to the grid point in question, i.e. $\partial \rho _B/\partial z |_{\rho (x,y,z,t)}$, as discussed in Arthur et al. (Reference Arthur, Venayagamoorthy, Koseff and Fringer2017). Overall, however, we believe that figures 3 and 4 support the claim that $\chi _{{loc}}$, as defined in (3.9), is largely satisfactory as a diagnostic for local mixing, even when distinct overturnings are present in the flow.

3.4. Local behaviour of mixing parameters

The behaviour of mixing efficiency discussed above supports a multi-phase description of turbulent flow evolution for KHI, comprising a period of highly efficient but variable early mixing as the primary billow breaks down, followed by a period of generic, approximately constant, energetic mixing in which the turbulence becomes increasingly isotropic, and finally a period of decay. We have shown that the mixing behaviour does not appear to depend on the presence of the ambient stratification in class L simulations, but for practical purposes, it is important to consider the properties of the flow within the turbulent layer that might be used to calculate mixing rates from observations.

Two commonly studied parameters are the buoyancy Reynolds number ${Re}_b$ and the gradient Richardson number ${Ri}_g$, defined locally here by horizontally averaging:

(3.14a,b)\begin{equation} {Ri}_g(z,t) \equiv \frac{N^2}{S^2} = {Ri}_0 \frac{-{\rm d}\bar{\rho}/{\rm d}z}{({\rm d}\bar{u}/{\rm d}z)^2},\quad \overline{{Re}_b}(z,t) \equiv \frac{\bar{\varepsilon}(z,t)}{(1/{Re})N^2}. \end{equation}

We use the momentum thickness $\ell _u$ defined in (3.1) as a measure of the height of the turbulent mixing layer and investigate the behaviour of these parameters within the region of each simulation defined by $-\ell _u/2 \leq z \leq \ell _u/2$. In a similar way to the plots of $\eta _{{loc}}$ in figure 3, we plot the frequency distribution of the values of ${Ri}_g(z,t)$ and $\overline {{Re}_b}(z,t)$ within the turbulent region at each time step in figures 5 and 6 , forming a 2-D histogram. We also plot the bulk values defined by

(3.15a,b)\begin{equation} {Ri}_b \equiv \frac{\langle N^2 \rangle_T}{\langle({\rm d}\bar{u}/{\rm d}z)^2\rangle_T },\quad {Re}_b \equiv \frac{\langle \varepsilon \rangle_T}{(1/{Re})\langle N^2\rangle_T}. \end{equation}

Figure 5. Two-dimensional histogram showing the evolution of vertical profiles of horizontally averaged buoyancy Reynolds number $\overline {{Re}_b}$ for simulations (a) T16, (b) L10, (c) T19 and (d) L13, where values are sampled over the mixing layer $-\ell _u/2 \leq z \leq \ell _u/2$. The dashed line shows the bulk value ${Re}_b$ averaged over the same interval.

Figure 6. Same as in figure 5 but for the gradient Richardson number ${Ri}_g$, with the dashed line showing the bulk value ${Ri}_b$ averaged over the mixing layer. The thin solid line indicates the evolution of the value of ${Ri}_g(z=0)$.

Looking first at the distribution of $\overline {{Re}_b}$ in figure 5, we see that the evolution is really quite similar for mixing layers of comparable heights, i.e. T16 and L10, as well as T19 and L13. During the period of most intense turbulence, there is significant variation in the local values of ${Re}_b$ which can become as large as $1000$. This maximum value is broadly consistent across all of the simulations suggesting a similarity in the most energetic turbulence produced that is not captured so explicitly in the bulk values shown by the dashed lines, which are noticeably lower for the more strongly stratified flows. Extremal values occur where large local values of dissipation coincide with regions of weak stratification $N^2$, as might be inferred by looking at figures 5 and 6 together with figure 2. There is also a strong similarity between all of the flows during the decay period.

Figure 6 shows that the distribution of values of ${Ri}_g$ within the mixing layer differs depending on the presence on the far field stratification. It is seen that, in general, L simulations exhibit larger values of ${Ri}_g$ throughout the entire flow evolution which leads to a greater bulk average as shown, though this does not appear to have any significant effect on the behaviour of the mixing. At early non-dimensional times both L and T simulations exhibit an increased frequency in small values of ${Ri}_g < 0.25$, suggesting values of this parameter in the regions of most intense mixing are not affected by the far field stratification. In particular, the value of ${Ri}_g$ on the centreline $z=0$ is similar across all of the simulations during this period. For larger $t$, the distributions of ${Ri}_g$ are broader and, in general, contain a higher concentration of larger values for L simulations, despite the similarity in mixing efficiency between T and L simulations during this period. Note that the behaviour of ${Ri}_g$ observed here is very different from the apparent self-organised criticality observed by Salehipour et al. (Reference Salehipour, Peltier and Caulfield2018) for flows in which the density interface is much sharper than the velocity interface at the centre of the shear layer, where the horizontally averaged state seems to be attracted towards values of ${Ri}_g\sim 1/4$.

It is commonly argued that mixing efficiency should depend on both ${Ri}_g$ and ${Re}_b$ (e.g. Mater & Venayagamoorthy Reference Mater and Venayagamoorthy2014; Salehipour & Peltier Reference Salehipour and Peltier2015; Salehipour, Caulfield & Peltier Reference Salehipour, Caulfield and Peltier2016a; Salehipour et al Reference Salehipour, Peltier, Whalen and MacKinnon2016b), which are usually obtained by averaging. Even ignoring the possibility that these two parameters may actually be correlated during a transient mixing event, (see Caulfield (Reference Caulfield2021) for a further discussion) figures 5 and 6 demonstrate that care should be applied when adopting such a two-parameter approach in the case of shear layers as taking an average may obscure local behaviour that would otherwise indicate the presence of similar mixing. Our findings support the argument that as long as there exists a period of intense mixing that is weakly affected by stratification (as characterised by the presence of small local values of ${Ri}_g$ and large values of $\overline {{Re}_b}$), the subsequent more isotropic period of roughly constant mixing efficiency it produces is generic, with little dependence on the presence of an ambient stratification that acts to increase values of ${Ri}_g$. With this in mind, it is perhaps more instructive to characterise mixing using physical length scales in the flow.

3.5. Length scale analysis

Intensive mixing regimes in the ocean are often associated with large overturnings, as characterised by an associated time-evolving physical length scale. The Thorpe scale $L_T$ is a measure of the mean vertical displacement of fluid parcels, calculated by sorting the density field into a statically stable state and taking the root mean square of the difference between the sorted and original positions of the parcels. Here, we do this by sorting each individual vertical column in the plane $y=0$, calculating the root mean square parcel displacement in the region $-\ell _u/2\leq z \leq \ell _u/2$ and then taking the median over the resulting values, in a manner similar to that described by Smyth & Moum (Reference Smyth and Moum2001). We expect the resulting $L_T$ to be similar to a median taken over all vertical columns due to the fact that the largest differences in vertical column structure occur in the streamwise $x$ direction. Note that an alternatively defined Thorpe scale $L_T^{3\text{-}D}$ calculates the root mean square displacement of each parcel from its position in the sorted 3-D density field $\rho _B(z)$. The evolution of $L_T$ can be expected to be largely similar to that of $L_T^{3\hbox{-}D}$, the main difference being that the latter may be non-zero even when there are no distinct overturnings in the flow. For our purposes, it will suffice to say that the differences between $L_T$ and $L_T^{3\hbox{-}D}$ are not of central importance, as has more recently been discussed in Mashayek et al. (Reference Mashayek, Caulfield and Peltier2017). One advantage of using $L_T$ instead of $L_T^{3\hbox{-}D}$ is that the former may readily be calculated from localised profile measurements in the ocean, whereas the latter is only practical in the context of numerical models. In general, the Thorpe scale is a purely geometrical construct that does not explicitly depend on the properties of the flow.

A related scale describing the magnitude of turbulent density fluctuations is the Ellison scale, defined here by volume averaging over the turbulent layer as

(3.16)\begin{equation} L_{E}\equiv\frac{\langle (\rho')^2 \rangle_T ^{1/2}}{\langle| \partial \bar{\rho}/\partial {z} | \rangle_T}. \end{equation}

Here $L_E$ is appealing for the inference of mixing properties because it is a direct measure of the turbulent motions in the flow. Like $L_T^{3\hbox{-}D}$, it may be non-zero when there are no distinct overturnings within vertical fluid columns. In practice, estimating $L_E$ from observational data is more challenging than $L_T$ due to the fact that suitably high frequency time-series data are required (Cimatoribus et al. Reference Cimatoribus, van Haren and Gostiaux2014). Given they both describe variations in the density field, $L_T$ and $L_E$ can be expected to evolve in a similar manner and may be explicitly related under some circumstances (Mater, Schaad & Venayagamoorthy Reference Mater, Schaad and Venayagamoorthy2013).

Another length scale that captures intrinsic properties of the turbulence is the Ozmidov scale

(3.17) \begin{equation} L_O\equiv\left(\frac{\langle \varepsilon \rangle_T}{\langle N^2 \rangle_T^{3}}\right)^{1/2}, \end{equation}

characterising the largest scales at which the turbulence is not significantly affected by the stratification. It is common to use the ratio $R_{OT} = L_O/L_T$ as a proxy for the ‘age’ of a turbulent event, with larger values of $R_{OT}>1$ being associated with late-stage turbulence that does not contain any significant overturnings (e.g. Smyth & Moum Reference Smyth and Moum2000).

In order to relate the above length scales to relevant mixing parameters, it is necessary to make additional assumptions about the turbulent motions in the flow. Ijichi & Hibiya (Reference Ijichi and Hibiya2018) assume that the Thorpe scale $L_T$ is a good approximation for the size of the largest eddies responsible for most of the turbulence production, whose characteristic size $L$ and velocity $U$ are assumed to follow the inertial scaling $\langle \varepsilon \rangle _T \sim U^3/L$, and furthermore, that $L_T$ and $U$ also correspond to equivalent scales in the classical Prandtl mixing length model for momentum with diffusivity $K_m$ so that $K_m \sim UL_T \sim \langle \varepsilon \rangle _T^{1/3} L_T^{4/3}$ using the inertial scaling above. Then, assuming that the density diffusivity $K_\rho \sim K_m$, i.e. the turbulence is only weakly affected by stratification so that the turbulent Prandtl number ${Pr}_T = K_m/K_\rho \sim 1$, it follows from using the Osborn relation (1.1) and eliminating $\langle \varepsilon \rangle _T$ in favour of $L_O$ and $\langle N^2 \rangle _T$ that

(3.18)\begin{equation} \varGamma \sim \frac{K_\rho}{\langle \varepsilon\rangle_T \langle N^2 \rangle_T^{{-}1}} \sim R_{OT}^{{-}4/3}, \end{equation}

where the flux coefficient $\varGamma$ is defined here as $\varGamma \equiv \eta _{\chi }/(1-\eta _{\chi })$ with $\eta _{\chi }$ defined in (3.12a–c). Early during the evolution of KHI however, it can be argued that whilst the mixing length may be well approximated by the overturning scale $L_T$, most of the turbulence production comes from smaller eddies of size $L_O$ that are not strongly affected by the stratification, so that the relevant inertial scaling for dissipation is $\langle \varepsilon \rangle _T \sim U^3/L_O$ and, hence, $K_m \sim \langle \varepsilon \rangle _T^{1/3}L_T L_O^{1/3}$. Still assuming that $K_m\sim K_\rho$, Mashayek et al. (Reference Mashayek, Caulfield and Alford2021) derive the alternative scaling

(3.19)\begin{equation} \varGamma \sim R_{OT}^{{-}1}. \end{equation}

We investigate the applicability of (3.18) and (3.19) in figure 7 by comparing plots of $\varGamma$ against $R_{OT}$ and $R_{OE}=L_O/L_E$, also looking at how the relationship depends on the turbulent Prandtl number ${Pr}_T \equiv \langle {Ri}_g \rangle _T /\eta _\chi$ (note that this definition has been shown by Salehipour & Peltier (Reference Salehipour and Peltier2015) to be equivalent to $K_m/K_\rho$ when we understand mixing as being associated with the evolution of the sorted background density profile $\rho _B$).

Figure 7. Scatter log plots showing the relationship between $\varGamma$ and (a) $R_{OT}$; (b) $R_{OE}$ for all of the simulations we consider. The colour of the markers indicates the value of the turbulent Prandtl number ${Pr}_T$, whilst the solid lines display the stated scaling relations. The flow of non-dimensional time $t$ is indicated by the arrow in (a). Note the difference in limits between the horizontal axes.

We see that the behaviour of $R_{OT}$ and $R_{OE}$ is similar as expected, with both ratios in general increasing as the large overturnings associated with the initial billow are destroyed by turbulence and the flow relaminarises. The initial transient growth in $\varGamma$ occurs whilst the flow is still mostly pre-turbulent and, hence, is not of interest for examining the above scalings. From figure 7(a) we see that the scaling (3.18) is observed to fit the data from all of the simulations remarkably well, even when the assumption that ${Pr}_T\sim 1$ fails to be appropriate at later non-dimensional times.

This is perhaps fortuitous; if we use $L_E$ instead of $L_O$ and look at $R_{OE}$ as shown in figure 7(b), we observe more nuanced behaviour which is highlighted by plotting both (3.18) and (3.19) on the same figure. At early non-dimensional times, there is an indication that $R_{OE}$ increases more quickly with decreasing $\varGamma$ so that the scaling (3.19) is perhaps a more appropriate fit, in line with the physical reasoning above. We include the relevant slope for reference, although there is a lot of scatter, and additional data would be required to draw any firm conclusions about this early regime. As the turbulence develops and $R_{OE}$ increases, the gradient steepens and the scaling (3.18) becomes more apparent.

In addition to the shallower $\varGamma$-$R_{OE}$ slope that exists early on, late time behaviour in figure 7(b) reasonably fits a $\varGamma \sim R_{OE}^{-2}$ scaling which has recently been derived by Howland, Taylor & Caulfield (Reference Howland, Taylor and Caulfield2020) for flows in a moderately stratified regime. Their argument, though we do not repeat it here, is based on the hypothesis that both the dominant buoyancy and turbulent time scales may affect the flow in this regime, corresponding to times in our simulations when turbulence persists but is decaying and values of the local stratification characterised by ${Ri}_g$ start to increase within the mixing layer. It is worth noting that Garanaik & Venayagamoorthy (Reference Garanaik and Venayagamoorthy2019) predict the alternative scaling $\varGamma \sim R_{OE}^{-1}$ in the same regime. The difference in these results may be due to the overlapping of flow regimes, where dynamics are affected by a combination of scales that depend on whether the buoyancy or turbulence dominates (indeed, data from the forced simulations of Shih et al. (Reference Shih, Koseff, Ivey and Ferziger2005) displayed in Garanaik & Venayagamoorthy (Reference Garanaik and Venayagamoorthy2019) appear to fit a $\varGamma \sim R_{OE}^{-2}$ scaling better in the moderately stratified regime, in contrast to the other DNS considered in the same study). It is also clear from the early time behaviour in figure 7(b) that the transition from one regime to another is gradual, with no distinct separation between the scalings. Understanding the behaviour of different flows in such overlapping or transitional intermediate regimes is an important motivation for future studies.

We propose that the main reason $\varGamma \sim R_{OE}^{-4/3}$ is more sensitive to the value of ${Pr}_T$ is that the Ellison scale directly captures the effect of the stratification in the flow, a feature that the Thorpe scale cannot replicate due to its inherently geometrical construction. We have already seen that, at least for the simulations we consider here, there is weak dependence of the later, generic mixing on the stratification as characterised by ${Ri}_g$ which may explain why $\varGamma \sim R_{OT}^{-4/3}$ holds reasonably well even after ${Pr}_T$ grows larger than unity. However, once the turbulence starts to decay, and larger local values of ${Ri}_g$ become more frequent within the mixing layer, it is highly plausible that the relevant physical scales will become influenced by buoyancy as captured by the denominator in the Ellison scale. At least from a fluid dynamics perspective, figure 7 suggests caution when using $L_T$ as the only length scale to describe overturning motions in a turbulent flow because it fails to capture properly the underlying physics, in particular the effect of the stratification. Further investigation is needed to assess the scalings discussed above in flows where the mixing efficiency is more heavily influenced by the stratification.