Published online by Cambridge University Press: 16 December 2015
We consider here the effects of inertia on the instability of a flat liquid film under the effects of capillary and intermolecular forces (van der Waals interaction). Firstly, we perform a linear stability analysis within the long-wave approximation, which shows that the inclusion of inertia does not produce new regions of instability other than the one previously known from the usual lubrication case. The wavelength, 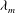 ${\it\lambda}_{m}$, corresponding to the maximum growth,
${\it\lambda}_{m}$, corresponding to the maximum growth, 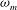 ${\it\omega}_{m}$ and the critical (marginal) wavelength do not change. The most affected feature of the instability under an increase of the Laplace number is the noticeable decrease of the growth rates of the unstable modes. In order to put in evidence the effects of the bidimensional aspects of the flow (neglected in the long-wave approximation), we also calculate the dispersion relation of the instability from the linearized version of the complete Navier–Stokes (N–S) equations. Unlike the long-wave approximation, the bidimensional model shows that
${\it\omega}_{m}$ and the critical (marginal) wavelength do not change. The most affected feature of the instability under an increase of the Laplace number is the noticeable decrease of the growth rates of the unstable modes. In order to put in evidence the effects of the bidimensional aspects of the flow (neglected in the long-wave approximation), we also calculate the dispersion relation of the instability from the linearized version of the complete Navier–Stokes (N–S) equations. Unlike the long-wave approximation, the bidimensional model shows that 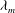 ${\it\lambda}_{m}$ can vary significantly with inertia when the aspect ratio of the film is not sufficiently small. We also perform numerical simulations of the nonlinear N–S equations and analyse to which extent the linear predictions can be applied depending on both the amount of inertia involved and the aspect ratio of the film.
${\it\lambda}_{m}$ can vary significantly with inertia when the aspect ratio of the film is not sufficiently small. We also perform numerical simulations of the nonlinear N–S equations and analyse to which extent the linear predictions can be applied depending on both the amount of inertia involved and the aspect ratio of the film.