Published online by Cambridge University Press: 06 October 2015
Direct numerical simulations based on high-resolution pseudospectral methods are carried out for detailed investigation into the instabilities arising in a differentially heated, rotating annulus, the baroclinic cavity. Following previous works using air (Randriamampianina et al., J. Fluid Mech., vol. 561, 2006, pp. 359–389), a liquid defined by Prandtl number 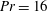 $Pr=16$ is considered in order to better understand, via the Prandtl number, the effects of fluid properties on the onset of gravity waves. The computations are particularly aimed at identifying and characterizing the spontaneously emitted small-scale fluctuations occurring simultaneously with the baroclinic waves. These features have been observed as soon as the baroclinic instability sets in. A three-term decomposition is introduced to isolate the fluctuation field from the large-scale baroclinic waves and the time-averaged mean flow. Even though these fluctuations are found to propagate as packets, they remain attached to the background baroclinic waves, locally triggering spatio-temporal chaos, a behaviour not observed with the air-filled cavity. The properties of these features are analysed and discussed in the context of linear theory. Based on the Richardson number criterion, the characteristics of the generation mechanism are consistent with a localized instability of the shear zonal flow, invoking resonant over-reflection.
$Pr=16$ is considered in order to better understand, via the Prandtl number, the effects of fluid properties on the onset of gravity waves. The computations are particularly aimed at identifying and characterizing the spontaneously emitted small-scale fluctuations occurring simultaneously with the baroclinic waves. These features have been observed as soon as the baroclinic instability sets in. A three-term decomposition is introduced to isolate the fluctuation field from the large-scale baroclinic waves and the time-averaged mean flow. Even though these fluctuations are found to propagate as packets, they remain attached to the background baroclinic waves, locally triggering spatio-temporal chaos, a behaviour not observed with the air-filled cavity. The properties of these features are analysed and discussed in the context of linear theory. Based on the Richardson number criterion, the characteristics of the generation mechanism are consistent with a localized instability of the shear zonal flow, invoking resonant over-reflection.