Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Winters, Kraig B.
and
de la Fuente, Alberto
2012.
Modelling rotating stratified flows at laboratory-scale using spectrally-based DNS.
Ocean Modelling,
Vol. 49-50,
Issue. ,
p.
47.
Winters, Kraig B.
and
Armi, Laurence
2013.
The response of a continuously stratified fluid to an oscillating flow past an obstacle.
Journal of Fluid Mechanics,
Vol. 727,
Issue. ,
p.
83.
Nasr-Azadani, Mohamad M.
and
Meiburg, Eckart
2014.
Influence of seafloor topography on the depositional behavior of bi-disperse turbidity currents: a three-dimensional, depth-resolved numerical investigation.
Environmental Fluid Mechanics,
Vol. 14,
Issue. 2,
p.
319.
Winters, Kraig B.
and
Armi, Laurence
2014.
Topographic control of stratified flows: upstream jets, blocking and isolating layers.
Journal of Fluid Mechanics,
Vol. 753,
Issue. ,
p.
80.
Nasr-Azadani, M. M.
and
Meiburg, E.
2014.
Turbidity currents interacting with three-dimensional seafloor topography.
Journal of Fluid Mechanics,
Vol. 745,
Issue. ,
p.
409.
Bosco, M.
and
Meunier, P.
2014.
Three-dimensional instabilities of a stratified cylinder wake.
Journal of Fluid Mechanics,
Vol. 759,
Issue. ,
p.
149.
Winters, Kraig B.
2016.
The turbulent transition of a supercritical downslope flow: sensitivity to downstream conditions.
Journal of Fluid Mechanics,
Vol. 792,
Issue. ,
p.
997.
Arneborg, Lars
Jansson, Pär
Staalstrøm, André
and
Broström, Göran
2017.
Tidal Energy Loss, Internal Tide Radiation, and Local Dissipation for Two-Layer Tidal Flow over a Sill.
Journal of Physical Oceanography,
Vol. 47,
Issue. 7,
p.
1521.
Mayer, F. T.
and
Fringer, O. B.
2017.
An unambiguous definition of the Froude number for lee waves in the deep ocean.
Journal of Fluid Mechanics,
Vol. 831,
Issue. ,
Ma, Weizhuang
Li, Yunbo
Ding, Yong
Hu, Kaiye
and
Lan, Linxin
2018.
Numerical Simulations of Linearly Stratified Flow Past Submerged Bodies.
Polish Maritime Research,
Vol. 25,
Issue. s3,
p.
68.
Nasr-Azadani, Mohamad M.
Meiburg, Eckart
and
Kneller, Benjamin
2018.
Mixing dynamics of turbidity currents interacting with complex seafloor topography.
Environmental Fluid Mechanics,
Vol. 18,
Issue. 1,
p.
201.
Meiburg, Eckart
and
Nasr-Azadani, Mohamad M.
2018.
Mixing and Dispersion in Flows Dominated by Rotation and Buoyancy.
Vol. 580,
Issue. ,
p.
129.
Jagannathan, Arjun
Winters, Kraig B.
and
Armi, Laurence
2020.
The effect of a strong density step on blocked stratified flow over topography.
Journal of Fluid Mechanics,
Vol. 889,
Issue. ,
Inoue, Ryuichiro
Tanaka, Takahiro
Nakamura, Hirohiko
Yanagimoto, Daigo
Fujio, Shinzou
and
Yasuda, Ichiro
2020.
Microstructure and Mooring Observations of Enhanced Mixing in the Kerama Gap.
Journal of Geophysical Research: Oceans,
Vol. 125,
Issue. 8,
Baker, L.E.
and
Mashayek, A.
2021.
Surface reflection of bottom generated oceanic lee waves.
Journal of Fluid Mechanics,
Vol. 924,
Issue. ,
KITANO, Yoshikazu
HATTORI, Yasuo
and
YAMADA, Tomohito J.
2021.
HYDRAULIC DESCRIPTION OF DOWNSLOPE WINDSTORMS UNDER NON-SHEAR AND CONTINUOUSLY STRATIFIED FLOW CONDITION.
Journal of Japan Society of Civil Engineers, Ser. B1 (Hydraulic Engineering),
Vol. 77,
Issue. 2,
p.
I_1315.
Legg, Sonya
2021.
Mixing by Oceanic Lee Waves.
Annual Review of Fluid Mechanics,
Vol. 53,
Issue. 1,
p.
173.
Deng, Jian
and
Kandel, Prabal
2022.
Drag force on a circular cylinder in stratified flow: A two-dimensional numerical study.
Physics of Fluids,
Vol. 34,
Issue. 5,
Chen, Jia-Lin
Yu, Xiao
Chang, Ming-Huei
Jan, Sen
Yang, Yiing Jang
and
Lien, Ren-Chieh
2022.
Shear Instability and Turbulent Mixing in the Stratified Shear Flow Behind a Topographic Ridge at High Reynolds Number.
Frontiers in Marine Science,
Vol. 9,
Issue. ,
Zemskova, Varvara E.
and
Grisouard, Nicolas
2022.
Energetics and Mixing of Stratified, Rotating Flow over Abyssal Hills.
Journal of Physical Oceanography,
Vol. 52,
Issue. 6,
p.
1155.
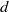 are run for different values of the approach Froude number
are run for different values of the approach Froude number 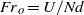 between
between 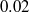 and
and 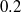 at
at 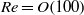 . The observed flow is characterized by blocking and upstream influence in front of the cylinder and by relatively thin, fast jets over the top and bottom of the cylinder. This continuously stratified flow can be understood in terms of an inviscid non-diffusive integral inertia–buoyancy balance reminiscent of reduced-gravity single-layer hydraulics, but one where the reduced gravity is coupled to the thickness of the jets. The proposed theoretical framework describes the flow upstream of the obstacle and at its crest. The most important elements of the theory are the inclusion of upstream influence in the form of blocked flow within an energetically constrained depth range and the recognition that the flow well above and well below the active, accelerated layers is dynamically uncoupled. These constraints determine, through continuity, the transport in the accelerated layers. Combining these results with the observation that the flow is asymmetric around the cylinder, i.e. hydraulically controlled, allows us to determine the active layer thicknesses, the effective reduced gravity and thus all of the integral flow properties of the fast layers in good agreement with the numerically computed flows.
. The observed flow is characterized by blocking and upstream influence in front of the cylinder and by relatively thin, fast jets over the top and bottom of the cylinder. This continuously stratified flow can be understood in terms of an inviscid non-diffusive integral inertia–buoyancy balance reminiscent of reduced-gravity single-layer hydraulics, but one where the reduced gravity is coupled to the thickness of the jets. The proposed theoretical framework describes the flow upstream of the obstacle and at its crest. The most important elements of the theory are the inclusion of upstream influence in the form of blocked flow within an energetically constrained depth range and the recognition that the flow well above and well below the active, accelerated layers is dynamically uncoupled. These constraints determine, through continuity, the transport in the accelerated layers. Combining these results with the observation that the flow is asymmetric around the cylinder, i.e. hydraulically controlled, allows us to determine the active layer thicknesses, the effective reduced gravity and thus all of the integral flow properties of the fast layers in good agreement with the numerically computed flows.