Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-25T06:20:24.807Z Has data issue: false hasContentIssue false
  • English
  • Français

High-speed boundary-layer transition induced by a discrete roughness element

Published online by Cambridge University Press:  24 July 2013

Prahladh S. Iyer  and
Krishnan Mahesh
Prahladh S. Iyer
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55455, USA
Krishnan Mahesh*
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55455, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulation (DNS) is used to study laminar to turbulent transition induced by a discrete hemispherical roughness element in a high-speed laminar boundary layer. The simulations are performed under conditions matching the experiments of Danehy et al. (AIAA Paper 2009–394, 2009) for free-stream Mach numbers of 3.37, 5.26 and 8.23. It is observed that the Mach 8.23 flow remains laminar downstream of the roughness, while the lower Mach numbers undergo transition. The Mach 3.37 flow undergoes transition closer to the bump when compared with Mach 5.26, in agreement with experimental observations. Transition is accompanied by an increase in 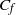${C}_{f} $ and 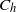${C}_{h} $ (Stanton number). Even for the case that did not undergo transition (Mach 8.23), streamwise vortices induced by the roughness cause a significant rise in 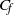${C}_{f} $ until 20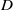$D$ downstream. The mean van Driest transformed velocity and Reynolds stress for Mach 3.37 and 5.26 show good agreement with available data. Temporal spectra of pressure for Mach 3.37 show that frequencies in the range of 10–1000 kHz are dominant. The transition process involves the following key elements: upon interaction with the roughness element, the boundary layer separates to form a series of spanwise vortices upstream of the roughness and a separation shear layer. The system of spanwise vortices wrap around the roughness element in the form of horseshoe/necklace vortices to yield a system of counter-rotating streamwise vortices downstream of the element. These vortices are located beneath the separation shear layer and perturb it, which results in the formation of trains of hairpin-shaped vortices further downstream of the roughness for the cases that undergo transition. These hairpins spread in the span with increasing downstream distance and the flow increasingly resembles a fully developed turbulent boundary layer. A local Reynolds number based on the wall properties is seen to correlate with the onset of transition for the cases considered.

JFM classification

Compressible Flows: Compressible boundary layers Instability: Transition to turbulence Aerodynamics: High-speed flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 729 , 25 August 2013 , pp. 524 - 562
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acarlar, M. S. & Smith, C. R. 1987 A study of hairpin vortices in a laminar boundary layer. Part 1. Hairpin vortices generated by a hemispherical protuberance. J. Fluid Mech. 175, 1–41.Google Scholar
Baker, C. J. 1979 The laminar horseshoe vortex. J. Fluid Mech. 95, 347–367.Google Scholar
Bartkowicz, M. D., Subbareddy, P. K. & Candler, G. V. 2010 Numerical simulations of roughness induced instability in the purdue mach 6 wind tunnel. AIAA Paper 2010-4723.CrossRefGoogle Scholar
Bathel, B. F., Danehy, P. M., Inman, J. A., Watkins, A. N., Jones, S. B., Lipford, W. E., Goodman, K. Z., Ivey, C.  B. & Goyne, C. P. 2010 Hypersonic laminar boundary layer velocimetry with discrete roughness on a flat plate. AIAA Paper 2010-4998.Google Scholar
Beresh, S. J., Henfling, J. F., Spillers, R. W. & Pruett, B. O. M. 2011 Fluctuating wall pressures measured beneath a supersonic turbulent boundary layer. Phys. Fluids 23, 075110.Google Scholar
Chang, C. & Choudhari, M. M. 2009 Hypersonic viscous flow over large roughness elements. AIAA Paper 2009-0173.Google Scholar
Chai, X. & Mahesh, K. 2011 Simulations of high speed turbulent jets in crossflows. AIAA Paper 2011-650.Google Scholar
Choi, H. & Moin, P. 1990 On the space–time characteristics of wall-pressure fluctuations. Phys. Fluids A 2, 1450.Google Scholar
Choudhari, M. M., Li, F., Wu, M., Chang, C., Edwards, J., Kegerise, M. & King, R. 2010 Laminar-turbulent transition behind discrete roughness elements in a high-speed boundary layer. AIAA Paper 2010-1575.Google Scholar
Coleman, G. N., Kim, J. & Moser, R. D. 1995 A numerical study of turbulent supersonic isothermal-wall channel flow. J. Fluid Mech. 305, 159–183.Google Scholar
Colonius, T. 2009 Modelling artificial boundary conditions for compressible flow. Annu. Rev. Fluid Mech. 36, 315–345.Google Scholar
Danehy, P. M., Bathel, B., Ivey, C., Inman, J. A. & Jones, S. B. 2009 NO PLIF study of hypersonic transition over a discrete hemispherical roughness element. AIAA Paper 2009-394.Google Scholar
Danehy, P. M., Garcia, A. P., Borg, S., Dyakonov, A. A., Berry, S. A., Inman, J. A. & Alderfer, D. W. 2007 Fluorescence visualization of hypersonic flow past triangular and rectangular boundary-layer trips. AIAA Paper 2007-0536.Google Scholar
Dong, H. & Zhong, X. 2002 High-order semi-implicit schemes for unsteady compressible flow simulations. AIAA J. 40 (5), 869–878.Google Scholar
Duan, L., Beekman, I. & Martin, M. P. 2010 Direct numerical simulation of hypersonic turbulent boundary layers. Part 2. Effect of wall temperature. J. Fluid Mech. 655, 419–445.Google Scholar
Ergin, F. G. & White, E. B. 2006 Unsteady and transitional flows behind roughness elements. AIAA J. 44 (11), 2504–2514.CrossRefGoogle Scholar
Groskopf, G., Kloker, M. J. & Marxen, O. 2008 Bi-global secondary stability theory for high-speed boundary layer flows. In Proceedings of the Summer Program, Center for Turbulence Research.Google Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P. 1988 Eddies, stream, and convergence zones in turbulent flows. Tech. Rep. CTR-S88. Center for Turbulence Research.Google Scholar
Klebanoff, P. S., Cleveland, W. G. & Tidstrom, K. D. 1992 On the evolution of a turbulent boundary layer induced by a three-dimensional roughness element. J. Fluid Mech. 237, 101–187.Google Scholar
Lees, L. & Lin, C. C. 1946 Investigation of the stability of the laminar boundary layer in a compressible fluid. In National Advisory Committee for Aeronautics, Washington, DC.Google Scholar
Mack, L. M. 1984 Boundary-layer linear stability theory. In AGARD Special Course on Stability and Transition of Laminar Flow.Google Scholar
Malik, M. R. 1990 Numerical methods for hypersonic boundary layer stability. J. Comput. Phys. 86 (2), 376–413.Google Scholar
Marxen, O., Iaccarino, G. & Shaqfeh, E. S. G. 2010 Disturbance evolution in a Mach 4.8 boundary layer with two-dimensional roughness-induced separation and shock. J. Fluid Mech. 648, 435–469.Google Scholar
Mason, P. J. & Morton, B. R. 1987 Trailing vortices in the wakes of surface-mounted obstacles. J. Fluid Mech. 175, 247–293.Google Scholar
Muppidi, S. & Mahesh, K. 2010 DNS of transition in supersonic boundary layers. AIAA Paper 2010-4440.Google Scholar
Muppidi, S. & Mahesh, K. 2011 DNS of unsteady shock boundary layer interaction. AIAA Paper 2011-724.Google Scholar
Muppidi, S. & Mahesh, K. 2012 Direct numerical simulations of roughness-induced transition in supersonic boundary layers. J. Fluid Mech. 693, 28–56.Google Scholar
Park, N. & Mahesh, K. 2007 Numerical and modelling issues in LES of compressible turbulent flows on unstructured grids. AIAA Paper 2007-722.Google Scholar
Pirozzoli, S. & Grasso, F. 2006 Direct numerical simulation of impinging shock waveturbulent boundary layer interaction at $M= 2. 25$ . Phys. Fluids 18, 065113.Google Scholar
Reda, D. C. 2002 Review and synthesis of roughness-dominated transition correlations for reentry applications. J. Spacecr. Rockets 39 (2), 161–167.Google Scholar
Redford, J. A., Sandham, N. D. & Roberts, G. T. 2010 Compressibility effects on boundary-layer transition induced by an isolated roughness element. AIAA J. 48 (12), 2818–2830.CrossRefGoogle Scholar
Reshotko, E. 2001 Transient growth: a factor in bypass transition. Phys. Fluids 13, 1067.Google Scholar
Reshotko, E. 2007 Is ${\mathit{Re}}_{\theta } / {M}_{e} $ a meaningful transition criterion? AIAA Paper 2007-943.Google Scholar
Reshotko, E. & Tumin, A. 2004 Role of transient growth in roughness-induced transition. AIAA J. 42 (4), 766–770.Google Scholar
Sakamoto, H. & Haniu, H. 1995 The formation mechanism and shedding frequency of vortices from a sphere in uniform shear flow. J. Fluid Mech. 287, 151–171.Google Scholar
Saric, W. S. 1994 Görtler vortices. Annu. Rev. Fluid Mech. 26, 379–409.Google Scholar
Saric, W. S., Reed, H. L. & White, E. B. 2003 Stability and transition of three-dimensional boundary layers. Annu. Rev. Fluid Mech. 35, 413–440.CrossRefGoogle Scholar
Schneider, S. P. 2008 Effects of roughness on hypersonic boundary-layer transition. J. Spacecr. Rockets 45 (2), 193–209.Google Scholar
Simpson, R. L. 2001 Junction flows. Annu. Rev. Fluid Mech. 33, 415–443.Google Scholar
Spalart, P. R. 1988 Direct simulation of turbulent boundary layer up to ${R}_{\theta } = 1410$ . J. Fluid Mech. 187, 61–98.Google Scholar
Tani, I., Komoda, H., Komatsu, Y. & Iuchi, M. 1962 Boundary-layer transition by isolated roughness. In Report No. 375. Aeronautical Research Institute, University of Tokyo.Google Scholar
Tumin, A. & Reshotko, E. 2005 Receptivity of a boundary-layer flow to a three-dimensional hump at finite Reynolds numbers. Phys. Fluids 17, 094101.CrossRefGoogle Scholar
Yee, H. C., Sandham, N. D. & Djomehri, M. J. 1999 Low-dissipative high-order shock-capturing methods using characteristic-based filters. J. Comput. Phys. 150 (1), 199–238.CrossRefGoogle Scholar
Zhong, X. 1998 High-order finite-difference schemes for numerical simulation of hypersonic boundary-layer transition. J. Comput. Phys. 144 (2), 662–709.CrossRefGoogle Scholar
Zhong, X. & Wang, X. 2012 Direct numerical simulation on the receptivity, instability, and transition of hypersonic boundary layers. Annu. Rev. Fluid Mech. 44, 527–561.Google Scholar