Published online by Cambridge University Press: 16 January 2023
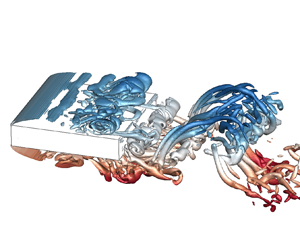
Large-eddy simulations of the unsteady flows around rectangular prisms with chord-to-depth ratios (B/D) ranging from 3 to 12 are carried out at a Reynolds number of 1000. A particular focus of the study is the physical mechanisms governing the global instability of the flow. The coherent structures and velocity spectra reveal that large-scale leading-edge vortices (L vortices) are formed by the coalescence of Kelvin–Helmholtz rollers. Based on dynamic mode decomposition, the interactions between the L vortex and the trailing-edge vortex (T vortex) at different B/D values are revealed. It is found that the phase difference between the L and T vortices is the critical factor promoting a stepwise increase in the Strouhal number with increasing B/D. According to the phase analysis, there are two types of pressure feedback-loop mechanisms maintaining the self-sustained oscillations. When B/D = 4–5, the feedback loop covers the separation region, and the global instability is controlled by the impinging shear-layer instability. When B/D = 3 and 6–12, the feedback loop covers the entire chord, and the global instability is controlled by the impinging leading-edge vortex shedding instability. Self-sustained oscillations of the shear layer still exist after a splitter plate is placed in the near wake, indicating that the T vortex shedding is not essential in triggering the global instability. Nevertheless, with the participation of the T vortex, the primary instability mode may be reselected due to the upper and lower limits of the shedding frequency imposed by the T vortex.