Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-25T16:26:12.221Z Has data issue: false hasContentIssue false
  • English
  • Français

A general description of a gravity current front propagating in a two-layer stratified fluid

Published online by Cambridge University Press:  28 September 2012

Brian L. White  and
Karl R. Helfrich
Brian L. White*
Affiliation:
Marine Sciences Department, UNC–Chapel Hill, NC 27599, USA
Karl R. Helfrich
Affiliation:
Department of Physical Oceanography, Woods Hole Oceanographic Institution, Woods Hole, MA 02543, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The behaviour of a gravity current propagating into a two-layer stratified ambient fluid is described in detail. A comprehensive description is given of the different flow regimes, with particular emphasis on the front condition linking the thickness of the gravity current to its speed of propagation and the transfer of energy to upstream disturbances in the form of internal bores and nonlinear solitary waves. Hydraulic theory analogous to that of two-layer flow over topography (Baines, J. Fluid Mech., vol. 146, 1984, pp. 127–167) is extended to the gravity current problem to classify frontal behaviour into the following regimes: Type I, subcritical currents; Type II, currents that generate upstream undular bores; Type III, currents that generate an upstream monotonic bore connected by a rarefaction; Type IV, supercritical fronts with a large-amplitude trapped solitary-wave-like disturbance; and Type V, supercritical gravity currents. Over 200 two-dimensional Boussinesq–Euler simulations spanning a range of gravity current properties demonstrate good agreement, for both the behavioural regime and the front condition 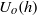, with hydraulic theory that extends original work by Rottman & Simpson (Q. J. R. Meteorol. Soc., vol. 115, 1989, pp. 941–963) to arbitrary ambient layer thickness, and uses an improved closure for the upstream bore that correctly predicts the behaviour in the limit of large bore amplitude. In addition, the energy balance is analysed, and it is shown that the energy transfer from the gravity current to upstream disturbances is significant, and consistent with the hydraulic theory. The results demonstrate a clear connection to the problem of upstream resonance in two-layer flow over topography, and have significant implications for interpreting field observations of nonlinear internal waves generated by atmospheric density currents and coastal river plumes.

JFM classification

Geophysical and Geological Flows: Gravity currents Geophysical and Geological Flows: Hydraulic control Geophysical and Geological Flows: Internal waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 711 , 25 November 2012 , pp. 545 - 575
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Baines, P. G. 1984 A unified description of two-layer flow over topography. J. Fluid Mech. 146, 127–167.CrossRefGoogle Scholar
2. Baines, P. G. 1995 Topographic Effects in Stratified Flows. Cambridge University Press.Google Scholar
3. Bell, J. B. & Marcus, D. L. 1992 A second-order projection method for variable-density flows. J. Comput. Phys. 101, 334–348.CrossRefGoogle Scholar
4. Benjamin, T. 1968 Gravity currents and related phenomena. J. Fluid Mech. 31, 209–248.CrossRefGoogle Scholar
5. Brown, D. J. & Christie, D. R. 1998 Fully nonlinear solitary waves in continuously stratified incompressible Boussinesq fluids. Phys. Fluids 10, 2569–2586.CrossRefGoogle Scholar
6. Camassa, R. & Tiron, R. 2011 Optimal two-layer approximation for continuous density stratification. J. Fluid Mech. 669, 32–54.CrossRefGoogle Scholar
7. Cheong, H.-B., Kuenen, J. J. P. & Linden, P. 2006 The front speed of intrusive gravity currents. J. Fluid Mech. 552, 1–11.CrossRefGoogle Scholar
8. Chu, V. H. & Baddour, R. E. 1977 Surges, waves and mixing in two-layer density stratified flow. In 17th Congress of the International Association on Hydraulic Research, Baden-Baden, Germany, pp. 303–310. IAHR.Google Scholar
9. Crook, N. 1983 The formation of the Morning Glory. In Mesoscale Meteorology: Theories, Observations, and Models (ed. Lilly, D. & Gal-Chen, T. ). D. Reidel.Google Scholar
10. Derzho, O. G. & Grimshaw, R. 1997 Solitary waves with a vortex core in a shallow layer of stratified fluid. Phys. Fluids 9, 3378–3385.CrossRefGoogle Scholar
11. Esler, J. G. & Pearce, J. D. 2011 Dispersive dam-break and lock-exchange flows in a two-layer fluid. J. Fluid Mech. 667, 555–585.CrossRefGoogle Scholar
12. Farmer, D. & Armi, L. 1999 The generation and trapping of solitary waves over topography. Science 283, 188–190.CrossRefGoogle ScholarPubMed
13. Flynn, M. R., Ungarish, M. & Tan, A. W. 2012 Gravity currents in a two-layer stratified ambient: the theory for the steady state (front condition) and lock-released flows, and experimental confirmations. Phys. Fluids 24, 026601.CrossRefGoogle Scholar
14. Grimshaw, R., Chan, K. & Chow, K. 2002 Transcritical flow of a stratified fluid: the forced extended Korteweg–de Vries model. Phys. Fluids 14, 755–774.CrossRefGoogle Scholar
15. Grimshaw, R. & Smyth, N. 1986 Resonant flow of a stratified fluid over topography. J. Fluid Mech. 169, 429–464.CrossRefGoogle Scholar
16. Grimshaw, R. & Yi, Z. 1991 Resonant generation of finite-amplitude waves by the flow of a uniformly stratified fluid over topography. J. Fluid Mech. 229, 603–628.CrossRefGoogle Scholar
17. Helfrich, K. & White, B. 2010 A model for large-amplitude internal solitary waves with trapped cores. Nonlinear Process. Geophys. 17, 303–318.CrossRefGoogle Scholar
18. Holyer, J. Y. & Huppert, H. E. 1980 Gravity currents entering a two-layer fluid. J. Fluid Mech. 100 (4), 739–767.CrossRefGoogle Scholar
19. Kilcher, L. F. & Nash, J. D. 2010 Structure and dynamics of the Columbia river tidal plume front. J. Geophys. Res.-Oceans 115, C00B12.CrossRefGoogle Scholar
20. King, S. E., Carr, M. & Dritschel, D. G. 2010 The steady-state form of large-amplitude internal solitary waves. J. Fluid Mech. 666, 477–505.CrossRefGoogle Scholar
21. Klemp, J., Rotunno, R. & Skamarock, W. 1997 On the propagation of internal bores. J. Fluid Mech. 331, 81–106.CrossRefGoogle Scholar
22. Lamb, K. G. 1994 Numerical experiments on internal wave generation by strong tidal flow across a finite amplitude bank edge. J. Geophys. Res. 99, 843–864.CrossRefGoogle Scholar
23. Lamb, K. G. 2000 Conjugate flows for a three-layer fluid. Physics of Fluids 12, 2169.CrossRefGoogle Scholar
24. Lamb, K. G. 2002 A numerical investigation of solitary internal waves with trapped cores formed via shoaling. J. Fluid Mech. 451, 109–144.CrossRefGoogle Scholar
25. Lamb, K. G. & Wilkie, K. P. 2004 Conjugate flows for waves with trapped cores. Phys. Fluids 16, 4685–4695.CrossRefGoogle Scholar
26. Lawrence, G. 1993 The hydraulics of steady two-layer flow over a fixed obstacle. J. Fluid Mech. 254, 605–633.CrossRefGoogle Scholar
27. Long, R. 1954 Some aspects of the flow of stratified fluids. Part 2. Experiments with a two-fluid system. Tellus 6, 97–115.CrossRefGoogle Scholar
28. Marino, B., Thomas, L. & Linden, P. 2005 The front condition for gravity currents. J. Fluid Mech. 536, 49–78.CrossRefGoogle Scholar
29. Maxworthy, T., Leilich, J., Simpson, J. E. & Meiburg, E. H. 2002 The propagation of a gravity current into a linearly stratified fluid. J. Fluid Mech. 453, 371–394.CrossRefGoogle Scholar
30. Melville, W. K. & Helfrich, K. R. 1987 Transcritical two-layer flow over topography. J. Fluid Mech. 178, 31–52.CrossRefGoogle Scholar
31. Moum, J., Nash, J. & Klymak, J. 2008 Small-scale processes in the coastal ocean. Oceanography 21 (4), 22–33.CrossRefGoogle Scholar
32. Munroe, J. R., Voegeli, C., Sutherland, B., Birman, V. & Meiburg, E. 2009 Intrusive gravity currents from finite-length locks in a uniformly stratified fluid. J. Fluid Mech. 635, 245–273.CrossRefGoogle Scholar
33. Nash, J. D., Kilcher, L. F. & Moum, J. N. 2009 Structure and composition of a strongly stratified, tidally pulsed river plume. J. Geophys. Res.-Oceans 114, C00B12.CrossRefGoogle Scholar
34. Nash, J. D. & Moum, J. N. 2005 River plumes as a source of large-amplitude internal waves in the coastal ocean. Nature 437, 400–403.CrossRefGoogle ScholarPubMed
35. Pan, J. & Jay, D. A. 2009 Dynamic characteristics and horizontal transports of internal solitons generated at the Columbia river plume front. Cont. Shelf Res. 29 (1), 252–262.CrossRefGoogle Scholar
36. Rottman, J. & Simpson, J. 1989 The formation of internal bores in the atmosphere: a laboratory model. Q. J. R. Meteorol. Soc. 115, 941–963.CrossRefGoogle Scholar
37. Simpson, J. E. 1997 Gravity Currents: In the Environment and the Laboratory, second edition. Cambridge University Press.Google Scholar
38. Stashchuk, N. & Vlasenko, V. 2009 Generation of internal waves by a supercritical stratified plume. J. Geophys. Res. 114 (C1), 1–17.CrossRefGoogle Scholar
39. Stastna, M. & Lamb, K. 2002 Large fully nonlinear internal solitary waves: the effect of background current. Phys. Fluids 14, 2987–2999.CrossRefGoogle Scholar
40. Stastna, M. & Peltier, W. R. 2005 On the resonant generation of large-amplitude internal solitary and solitary-like waves. J. Fluid Mech. 543, 267–292.CrossRefGoogle Scholar
41. Tan, A. W., Nobes, D. S., Fleck, B. A. & Flynn, M. R. 2011 Gravity currents in two-layer stratified media. Environ. Fluid Mech. 11, 203–223.CrossRefGoogle Scholar
42. Ungarish, M. 2006 On gravity currents in a linearly stratified ambient: a generalization of Benjamin’s steady-state propagation results. J. Fluid Mech. 548, 49–68.CrossRefGoogle Scholar
43. Ungarish, M. & Huppert, H. 2006 Energy balances for propagating gravity currents: homogeneous and stratified ambients. J. Fluid Mech. 565, 363–380.CrossRefGoogle Scholar
44. White, B. L. & Helfrich, K. R. 2008 Gravity currents and internal waves in a stratified fluid. J. Fluid Mech. 616, 327–356.CrossRefGoogle Scholar
45. Whitham, G. B. 1974 Linear and Nonlinear Waves. Wiley.Google Scholar
46. Wood, I. & Simpson, J. 1984 Jumps in layered miscible fluids. J. Fluid Mech. 140, 215–231.CrossRefGoogle Scholar
47. Yih, C. S. & Guha, C. R. 1955 Hydraulic jumps in a fluid system of two layers. Tellus 7, 358–366.CrossRefGoogle Scholar