Published online by Cambridge University Press: 14 October 2013
A recent numerical study by Rao et al. (J. Fluid Mech., vol. 717, 2013, pp. 1–29) predicted the existence of several previously unobserved linearly unstable three-dimensional modes in the wake of a spinning cylinder in cross-flow. While linear stability analysis suggests that some of these modes exist for relatively limited ranges of Reynolds numbers and rotation rates, this may not be true for fully developed nonlinear wakes. In the current paper, we present the results of water channel experiments on a rotating cylinder in cross-flow, for Reynolds numbers 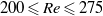 $200\leqslant \mathit{Re}\leqslant 275$ and non-dimensional rotation rates
$200\leqslant \mathit{Re}\leqslant 275$ and non-dimensional rotation rates 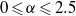 $0\leqslant \alpha \leqslant 2. 5$. Using particle image velocimetry and digitally post-processed hydrogen bubble flow visualizations, we confirm the existence of the predicted modes for the first time experimentally. For instance, for
$0\leqslant \alpha \leqslant 2. 5$. Using particle image velocimetry and digitally post-processed hydrogen bubble flow visualizations, we confirm the existence of the predicted modes for the first time experimentally. For instance, for 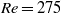 $\mathit{Re}= 275$ and a rotation rate of
$\mathit{Re}= 275$ and a rotation rate of 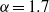 $\alpha = 1. 7$, we observe a subharmonic mode, mode C, with a spanwise wavelength of
$\alpha = 1. 7$, we observe a subharmonic mode, mode C, with a spanwise wavelength of 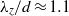 ${\lambda }_{z} / d\approx 1. 1$. On increasing the rotation rate, two modes with a wavelength of
${\lambda }_{z} / d\approx 1. 1$. On increasing the rotation rate, two modes with a wavelength of 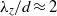 ${\lambda }_{z} / d\approx 2$ become unstable in rapid succession, termed modes D and E. Mode D grows on a shedding wake, whereas mode E consists of streamwise vortices on an otherwise steady wake. For
${\lambda }_{z} / d\approx 2$ become unstable in rapid succession, termed modes D and E. Mode D grows on a shedding wake, whereas mode E consists of streamwise vortices on an otherwise steady wake. For 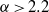 $\alpha \gt 2. 2$, a short-wavelength mode F appears localized close to the cylinder surface with
$\alpha \gt 2. 2$, a short-wavelength mode F appears localized close to the cylinder surface with 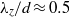 ${\lambda }_{z} / d\approx 0. 5$, which is presumably a manifestation of centrifugal instability. Unlike the other modes, mode F is a travelling wave with a spanwise frequency of
${\lambda }_{z} / d\approx 0. 5$, which is presumably a manifestation of centrifugal instability. Unlike the other modes, mode F is a travelling wave with a spanwise frequency of 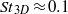 ${\mathit{St}}_{3D} \approx 0. 1$. In addition to these new modes, observations on the one-sided shedding process, known as the ‘second shedding’, are reported for
${\mathit{St}}_{3D} \approx 0. 1$. In addition to these new modes, observations on the one-sided shedding process, known as the ‘second shedding’, are reported for 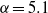 $\alpha = 5. 1$. Despite suggestions from the literature, this process seems to be intrinsically three-dimensional. In summary, our experiments confirm the linear predictions by Rao et al., with very good agreement of wavelengths, symmetries and the phase velocity for the travelling mode. Apart from this, these experiments examine the nonlinear saturated state of these modes and explore how the existence of multiple unstable modes can affect the selected final state. Finally, our results establish that several distinct three-dimensional instabilities exist in a relatively confined area on the
$\alpha = 5. 1$. Despite suggestions from the literature, this process seems to be intrinsically three-dimensional. In summary, our experiments confirm the linear predictions by Rao et al., with very good agreement of wavelengths, symmetries and the phase velocity for the travelling mode. Apart from this, these experiments examine the nonlinear saturated state of these modes and explore how the existence of multiple unstable modes can affect the selected final state. Finally, our results establish that several distinct three-dimensional instabilities exist in a relatively confined area on the 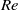 $\mathit{Re}$–
$\mathit{Re}$– $\alpha $ parameter map, which could account for their non-detection previously.
$\alpha $ parameter map, which could account for their non-detection previously.
This video shows all investigated three-dimensional modes in sequence at Re=275, when spinning up the cylinder slowly from α=0 to α=4. The hydrogen bubbles wire is placed upstream and parallel to the cylinder; a laser sheet is used for illumination. Initially, mode B can be seen in the non-rotating cylinder wake, and for very low rotation rates. The subharmonic mode C becomes very clear at α>1.2. Modes D and E follow in quick succession at around 1.8<α<2. Mode E appears suddenly at α≈2.1 on the surface of the cylinder, and persists until α=4. The laser is moved slowly in cross-stream direction to show the structure of the wake more clearly.
The rotating cylinder wake is shown at Re=200, α=4.5. For these conditions, two-dimensional one-sided shedding (`second shedding' or `mode II') have been described by other researchers. The present video shows a highly three-dimensional wake and the absence of two-dimensional periodic shedding.
The rotating cylinder wake at Re=100, α=5.1 shows the detachment of several single-sided vortex bends, which resemble the `second shedding' mode described by other researchers. This video suggests that this process is highly three-dimensional. (The hydrogen bubbles wire is placed downstream and parallel to the cylinder.)