Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-03T00:24:12.261Z Has data issue: false hasContentIssue false
  • English
  • Français

Entry and exit flows in curved pipes

Published online by Cambridge University Press:  23 February 2017

Jesse T. Ault Open the ORCID record for Jesse T. Ault [Opens in a new window] ,
Bhargav Rallabandi Open the ORCID record for Bhargav Rallabandi [Opens in a new window] ,
Orest Shardt ,
Kevin K. Chen Open the ORCID record for Kevin K. Chen [Opens in a new window]  and
Howard A. Stone
Jesse T. Ault
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
Bhargav Rallabandi
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
Orest Shardt
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
Kevin K. Chen
Affiliation:
Department of Aerospace and Mechanical Engineering, University of Southern California, Los Angeles, CA 90089, USA
Howard A. Stone*
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Solutions are presented for both laminar developing flow in a curved pipe with a parabolic inlet velocity and laminar transitional flow downstream of a curved pipe into a straight outlet. Scalings and linearized analyses about appropriate base states are used to show that both cases obey the same governing equations and boundary conditions. In particular, the governing equations in the two cases are linearized about fully developed Poiseuille flow in cylindrical coordinates and about Dean’s velocity profile for curved pipe flow in toroidal coordinates respectively. Subsequently, we identify appropriate scalings of the axial coordinate and disturbance velocities that eliminate dependence on the Reynolds number 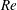$Re$ and dimensionless pipe curvature $\unicode[STIX]{x1D6FC}$ from the governing equations and boundary conditions in the limit of small $\unicode[STIX]{x1D6FC}$ and large 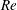$Re$. Direct numerical simulations confirm the scaling arguments and theoretical solutions for a range of 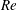$Re$ and $\unicode[STIX]{x1D6FC}$. Maximum values of the axial velocity, secondary velocity and pressure perturbations are determined along the curved pipe section. Results collapse when the scalings are applied, and the theoretical solutions are shown to be valid up to Dean numbers of 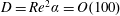$D=Re^{2}\unicode[STIX]{x1D6FC}=O(100)$. The developing flows are shown numerically and analytically to contain spatial oscillations. The numerically determined decay of the velocity perturbations is also used to determine entrance/development lengths for both flows, which are shown to scale linearly with the Reynolds number, but with a prefactor 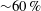${\sim}60\,\%$ larger than the textbook case of developing flow in a straight pipe.

JFM classification

Mathematical Foundations: General fluid mechanics Mathematical Foundations: Mathematical Foundations
Type
Papers
Information
Journal of Fluid Mechanics , Volume 815 , 25 March 2017 , pp. 570 - 591
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ault, J. T., Chen, K. K. & Stone, H. A. 2015 Downstream decay of fully developed Dean flow. J. Fluid Mech. 777, 219–244.CrossRefGoogle Scholar
Ault, J. T., Fani, A., Chen, K. K., Shin, S., Gallaire, F. & Stone, H. A. 2016 Vortex-breakdown-induced particle capture in branching junctions. Phys. Rev. Lett. 117 (8), 084501.CrossRefGoogle ScholarPubMed
Berger, S. A., Talbot, L. & Yao, L. S. 1983 Flow in curved pipes. Annu. Rev. Fluid Mech. 15, 461–512.CrossRefGoogle Scholar
Boutabaa, M., Helin, L., Mompean, G. & Thais, L. 2009 Numerical study of Dean vortices in developing Newtonian and viscoelastic flows through a curved duct of square cross-section. C. R. Méc. 337, 40–47.CrossRefGoogle Scholar
Dean, W. R. 1927 Note on the motion of fluid in a curved pipe. Phil. Mag. 20, 208–223.CrossRefGoogle Scholar
Dean, W. R. 1928 The stream-line motion of fluid in a curved pipe. Phil. Mag. 5, 673–695.CrossRefGoogle Scholar
Fairbank, J. A. & So, R. M. C. 1987 Upstream and downstream influence of pipe curvature on the flow through a bend. Intl J. Heat Fluid Flow 8, 211–217.CrossRefGoogle Scholar
Fox, R. W., Pritchard, P. J. & McDonald, A. T. 2009 Introduction to Fluid Mechanics, 7th edn. Wiley.Google Scholar
Gallaire, F., Ruith, M., Meiburg, E., Chomaz, J.-M. & Huerre, P. 2006 Spiral vortex breakdown as a global mode. J. Fluid Mech. 549, 71–80.CrossRefGoogle Scholar
Gresho, P. M. & Sani, R. L. 1987 On pressure boundary conditions for the incompressible Navier–Stokes equations. Intl J. Numer. Meth. Fluids 7, 1111–1145.CrossRefGoogle Scholar
Kluwick, A. & Wohlfart, H. 1984 Entry flow in weakly curved ducts. Ing.-Arch. 54, 107–120.CrossRefGoogle Scholar
Liu, S. & Masliyah, J. H. 1996 Steady developing laminar flow in helical pipes with finite pitch. Intl J. Comput. Fluid Dyn. 6, 209–224.CrossRefGoogle Scholar
Mohanty, A. K. & Asthana, S. B. L. 1978 Laminar flow in the entrance region of a smooth pipe. J. Fluid Mech. 90, 433–447.CrossRefGoogle Scholar
Olson, D. E. & Snyder, B. 1985 The upstream scale of flow development in curved circular pipes. J. Fluid Mech. 150, 139–158.CrossRefGoogle Scholar
Singh, M. P. 1974 Entry flow in a curved pipe. J. Fluid Mech. 65, 517–539.CrossRefGoogle Scholar
Singh, M. P., Sinha, P. C. & Aggarwal, M. 1978 Flow in the entrance of the aorta. J. Fluid Mech. 87, 97–120.CrossRefGoogle Scholar
Smith, F. T. 1976 Fluid flow into a curved pipe. Proc. R. Soc. Lond. A 351, 71–87.Google Scholar
Smith, F. T. & Duck, P. W. 1980 On the severe non-symmetric constriction, curving or cornering of channel flows. J. Fluid Mech. 90, 727–753.CrossRefGoogle Scholar
So, R. M. C. 1976 Entry flow in curved channels. Trans. ASME J. Fluids Engng 98, 305–310.CrossRefGoogle Scholar
Tadjfar, M. & Smith, F. T. 2004 Direct simulations and modelling of basic three-dimensional bifurcating tube flows. J. Fluid Mech. 519, 1–32.CrossRefGoogle Scholar
Wang, S. & Rusak, Z. 1997 The dynamics of a swirling flow in a pipe and transition to axisymmetric vortex breakdown. J. Fluid Mech. 340, 177–223.CrossRefGoogle Scholar
Weller, H. H., Tabor, G., Jasak, H. & Fureby, C. 1998 A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 12, 620–631.CrossRefGoogle Scholar
White, F. M. 2005 Viscous Fluid Flow, 3rd edn. McGraw-Hill.Google Scholar
Yao, L. S. & Berger, S. A. 1975 Entry flow in a curved pipe. J. Fluid Mech. 67, 177–196.CrossRefGoogle Scholar