Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-27T07:25:41.976Z Has data issue: false hasContentIssue false
  • English
  • Français

Entrainment in two coalescing axisymmetric turbulent plumes

Published online by Cambridge University Press:  11 July 2014

C. Cenedese  and
P. F. Linden
C. Cenedese*
Affiliation:
Department of Physical Oceanography, Woods Hole Oceanographic Institution, MS#21, 360 Woods Hole Road, Woods Hole, MA 02543, USA
P. F. Linden
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A model of the total volume flux and entrainment occurring in two coalescing axisymmetric turbulent plumes is developed and compared with laboratory experiments. The dynamical evolution of the two plumes is divided into three regions. In region 1, where the plumes are separate, the entrainment in each plume is unaffected by the other plume, although the two plumes are drawn together due to the entrainment of ambient fluid between them. In region 2 the two plumes touch each other but are not yet merged. In this region the total entrainment is a function of both the dynamics of the touching plumes and the reduced surface area through which entrainment occurs. In region 3 the two plumes are merged and the entrainment is equivalent to that in a single plume. We find that the total volume flux after the two plumes touch and before they merge increases linearly with distance from the sources, and can be expressed as a function of the known total volume fluxes at the touching and merging heights. Finally, we define an ‘effective’ entrainment constant, 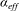$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\alpha _{eff}$, as the value of $\alpha $ needed to obtain the same total volume flux in two independent plumes as that occurring in two coalescing plumes. The definition of 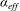$\alpha _{eff}$ allows us to find a single expression for the development of the total volume flux in the three different dynamical regions. This single expression will simplify the representation of coalescing plumes in more complex models, such as in large-scale geophysical convection, in which plume dynamics are not resolved. Experiments show that the model provides an accurate measure of the total volume flux in the two coalescing plumes as they evolve through the three regions.

JFM classification

Mixing: Mixing Convection: Plumes/thermals Mixing: Turbulent mixing
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 752 , 10 August 2014 , R2
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baines, W. D. 1983 A technique for the direct measurement of volume flux of a plume. J. Fluid Mech. 132, 247–256.Google Scholar
Baines, W. D. & Keffer, K. F. 1975 Entrainment by a multiple source turbulent jet. Adv. Geophys. 18(b), 289–298.CrossRefGoogle Scholar
Baker, E. T., German, C. R. & Elderfield, H. 1995 Hydrothermal plumes over spreading-center axes: global distributions and geological inferences. In Seafloor Hydrothermal Systems: Physical, Chemical, Biological, and Geological Interactions (ed. Humphris, S. E., Zierenberg, R. A., Mullineaux, L. S. & Thomson, R. E.), Geophys. Monogr. Ser., vol. 91, pp. 47–71. American Geophysical Union.Google Scholar
Hunt, G. R. & Kaye, N. B. 2001 Virtual origin correction for lazy turbulent plumes. J. Fluid Mech. 435, 377–396.Google Scholar
Jenkins, A. 2011 Convection-driven melting near the grounding lines of ice shelves and tidewater glaciers. J. Phys. Oceanogr. 41, 2279–2294.CrossRefGoogle Scholar
Kaye, N. B. & Linden, P. F. 2004 Coalescing axisymmetric turbulent plumes. J. Fluid Mech. 502, 41–63.Google Scholar
Kimura, S., Holland, P. R., Jenkins, A. & Piggott, M. 2014 The effect of meltwater plumes on the melting of a vertical glacier face. J. Phys. Oceanogr. (submitted).CrossRefGoogle Scholar
Lai, A. C. H. & Lee, J. H. W. 2012 Dynamic interaction of multiple buoyant jets. J. Fluid Mech. 708, 539–575.CrossRefGoogle Scholar
Lee, J. H. W. 2012 Mixing of multiple buoyant jets. ASCE J. Hydraul. Engng 138, 1008–1021.Google Scholar
Linden, P. F. 1999 The fluid mechanics of natural ventilation. Annu. Rev. Fluid Mech. 31, 201–238.Google Scholar
Morton, B. R., Taylor, G. I. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. 234, 1–23.Google Scholar
Sciascia, R., Straneo, F., Cenedese, C. & Heimbach, P. 2013 Seasonal variability of submarine melt rate and circulation in an East Greenland fjord. J. Geophys. Res.: Oceans 118 (5), 2492–2506.Google Scholar
Speer, K. G. & Rona, P. A. 1989 A model of an Atlantic and Pacific hydrothermal plume. J. Geophys. Res.: Oceans 94 (C5), 6213–6220.CrossRefGoogle Scholar
Turner, J. S. 1979 Buoyancy Effects in Fluids. Cambridge University Press.Google Scholar
Xu, Y., Rignot, E., Fenty, I., Menemenlis, D. & Flexas, M. M. 2013 Subaqueous melting of Store Glacier, West Greenland from three-dimensional, high-resolution numerical modeling and ocean observations. Geophys. Res. Lett. 40 (17), 4648–4653.Google Scholar
Xu, Y., Rignot, E., Menemenlis, D. & Koppes, M. N. 2012 Numerical experiments on subaqueous melting of Greenland tidewater glaciers in response to ocean warming and enhanced subglacial runoff. Ann. Glaciol. 53 (60), 229–234.Google Scholar
Yannopoulos, P. C. & Noutsopoulos, G. C. 2006a Interaction of vertical round turbulent buoyant jets – part 1: entrainment restriction approach. J. Hydraul Res. 44 (2), 218–232.CrossRefGoogle Scholar
Yannopoulos, P. C. & Noutsopoulos, G. C. 2006b Interaction of vertical round turbulent buoyant jets – part 2: superposition method. J. Hydraul Res. 44 (2), 233–248.Google Scholar