Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-27T11:13:02.794Z Has data issue: false hasContentIssue false
  • English
  • Français

Electroviscous effects on the squeezing flow of thin electrolyte solution films

Published online by Cambridge University Press:  11 February 2020

Cunlu Zhao Open the ORCID record for Cunlu Zhao [Opens in a new window] ,
Wenyao Zhang Open the ORCID record for Wenyao Zhang [Opens in a new window] ,
Dirk van den Ende  and
Frieder Mugele
Cunlu Zhao*
Affiliation:
Key Laboratory of Thermo-Fluid Science and Engineering of MOE, Xi’an Jiaotong University, Xi’an710049, China
Wenyao Zhang
Affiliation:
Key Laboratory of Thermo-Fluid Science and Engineering of MOE, Xi’an Jiaotong University, Xi’an710049, China
Dirk van den Ende
Affiliation:
Physics of Complex Fluids, Faculty of Science and Technology, University of Twente, Enschede7500 AZ, The Netherlands
Frieder Mugele
Affiliation:
Physics of Complex Fluids, Faculty of Science and Technology, University of Twente, Enschede7500 AZ, The Netherlands
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

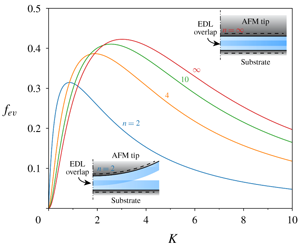
We present a detailed analysis of the electroviscous effect in the squeeze out of thin electrolyte films confined between two charged surfaces. The two charged surfaces consist of a curved surface and a flat surface, which closely simulate the tip–substrate configuration in the force measurement of electrolyte solutions with dynamic atomic force microscopy. In the lubrication limit, we find the analytical solution of the electroviscous-effect-modified squeezing flow field in the thin electrolyte film confined between the tip and substrate by solving the Nernst–Planck–Poisson/Navier–Stokes equation under the justified condition of pseudo-steadiness. We also derive the solution of the tip–substrate interaction, which comprises of a conservative electric double layer (EDL) force and an electroviscous-effect-enhanced dissipative hydrodynamic force. The current work focuses on the dissipative hydrodynamic force since the conservative EDL force has been well described by the well-known Derjaguin–Landau–Verwey–Overbeek theory. We introduce a power-law index ($n$) for the tip surface, which enables an unprecedented quantitative characterization of the tip profile effect on the electroviscous effect. We observe a seemingly counter-intuitive effect that, for a given tip–substrate separation, the electroviscous effect is the strongest at one particular value of the zeta ($\unicode[STIX]{x1D701}$) potential and diminishes as the $\unicode[STIX]{x1D701}$ potential departs from this value. We reveal the counterion conductivity of the EDL to be the governing factor for the electroviscous effect under a given $\unicode[STIX]{x1D701}$ potential. In addition to enhancing the dissipative hydrodynamic interaction force, the electroviscous effect modifies the velocity profiles in the thin electrolyte solution films such that they are much sharper.

JFM classification

Micro-/Nano-fluid dynamics: Microfluidics Drops and Bubbles: Electrohydrodynamic effects
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 888 , 10 April 2020 , A29
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adam, H., Rode, S., Schreiber, M., Kobayashi, K., Yamada, H. & Kühnle, A. 2014 Photothermal excitation setup for a modified commercial atomic force microscope. Rev. Sci. Instrum. 85, 023703.CrossRefGoogle ScholarPubMed
Albijanic, B., Ozdemir, O., Nguyen, A. V. & Bradshaw, D. 2010 A review of induction and attachment times of wetting thin films between air bubbles and particles and its relevance in the separation of particles by flotation. Adv. Colloid Interface Sci. 159, 1–21.CrossRefGoogle ScholarPubMed
Alexander, B. M. & Prieve, D. C. 1987 A hydrodynamic technique for measurement of colloidal forces. Langmuir 3, 788–795.CrossRefGoogle Scholar
Alizadeh, S. & Mani, A. 2017 Multiscale model for electrokinetic transport in networks of pores. Part I. Model derivation. Langmuir 33, 6205–6219.CrossRefGoogle ScholarPubMed
Aronson, M. P. & Princen, H. M. 1980 Contact angles associated with thin liquid films in emulsions. Nature 286, 370–372.CrossRefGoogle Scholar
Bazant, M. Z., Storey, B. D. & Kornyshev, A. A. 2011 Double layer in ionic liquids: overscreening versus crowding. Phys. Rev. Lett. 106, 046102.CrossRefGoogle ScholarPubMed
Behrens, S. H. & Grier, D. G. 2001 The charge of glass and silica surfaces. J. Chem. Phys. 115, 6716–6721.CrossRefGoogle Scholar
Bénichou, O., Cachile, M., Cazabat, A. M., Poulard, C., Valignat, M. P., Vandenbrouck, F. & Van Effenterre, D. 2003 Thin films in wetting and spreading. Adv. Colloid Interface Sci. 100–102, 381–398.CrossRefGoogle Scholar
Berger, G., Cadore, E., Schott, J. & Dove, P. M. 1994 Dissolution rate of quartz in lead and sodium electrolyte solutions between 25 and 300 °C: effect of the nature of surface complexes and reaction affinity. Geochim. Cosmochim. Acta 58, 541–551.CrossRefGoogle Scholar
Bhadauria, R. & Aluru, N. R. 2017 Multiscale modeling of electroosmotic flow: effects of discrete ion, enhanced viscosity, and surface friction. J. Chem. Phys. 146, 184106.Google Scholar
Bike, S. G., Lazarro, L. & Prieve, D. C. 1995 Electrokinetic lift of a sphere moving in slow shear flow parallel to a wall. I. Experiment. J. Colloid Interface Sci. 175, 411–421.CrossRefGoogle Scholar
Bike, S. G. & Prieve, D. C. 1990 Electrohydrodynamic lubrication with thin double layers. J. Colloid Interface Sci. 136, 95–112.CrossRefGoogle Scholar
Bike, S. G. & Prieve, D. C. 1992 Electrohydrodynamics of thin double layers: a model for the streaming potential profile. J. Colloid Interface Sci. 154, 87–96.CrossRefGoogle Scholar
Bike, S. G. & Prieve, D. C. 1995 Electrokinetic lift of a sphere moving in slow shear flow parallel to a wall. II. Theory. J. Colloid Interface Sci. 175, 422–434.CrossRefGoogle Scholar
Bo, Z. & Umehara, N. 1998 Hydrodynamic lubrication theory considering electric double layer for very thin water film lubrication of ceramics. JSME Intl J. C 41, 285–290.CrossRefGoogle Scholar
Bocquet, L. & Charlaix, E. 2010 Nanofluidics, from bulk to interfaces. Chem. Soc. Rev. 39, 1073–1095.CrossRefGoogle ScholarPubMed
Bonaccurso, E., Kappl, M. & Butt, H.-J. 2002 Hydrodynamic force measurements: boundary slip of water on hydrophilic surfaces and electrokinetic effects. Phys. Rev. Lett. 88, 076103.CrossRefGoogle ScholarPubMed
Borukhov, I., Andelman, D. & Orland, H. 1997 Steric effects in electrolytes: a modified Poisson–Boltzmann equation. Phys. Rev. Lett. 79, 435–438.CrossRefGoogle Scholar
Burgreen, D. & Nakache, F. R. 1964 Electrokinetic flow in ultrafine capillary slits. J. Phys. Chem. 68, 1084–1091.CrossRefGoogle Scholar
Chakraborty, J. & Chakraborty, S. 2011 Combined influence of streaming potential and substrate compliance on load capacity of a planar slider bearing. Phys. Fluids 23, 082004.CrossRefGoogle Scholar
Chun, B. & Ladd, A. J. C. 2004 The electroviscous force between charged particles: beyond the thin-double-layer approximation. J. Colloid Interface Sci. 274, 687–694.CrossRefGoogle ScholarPubMed
Cox, R. G. 1997 Electroviscous forces on a charged particle suspended in a flowing liquid. J. Fluid Mech. 338, 1–34.CrossRefGoogle Scholar
Craig, V. S. J. 2004 Bubble coalescence and specific-ion effects. Curr. Opin. Colloid Interface Sci. 9, 178–184.CrossRefGoogle Scholar
Craig, V. S. J. 2011 Do hydration forces play a role in thin film drainage and rupture observed in electrolyte solutions? Curr. Opin. Colloid Interface Sci. 16, 597–600.CrossRefGoogle Scholar
Craig, V. S. J., Neto, C. & Williams, D. R. M. 2001 Shear-dependent boundary slip in an aqueous Newtonian liquid. Phys. Rev. Lett. 87, 054504.CrossRefGoogle Scholar
Derjaguin, B. V., Churaev, N. V., Muller, V. M. & Kitchener, J. A. 1987 Surface Forces. Consultants Bureau.CrossRefGoogle Scholar
Eijkel, J. 2007 Liquid slip in micro- and nanofluidics: recent research and its possible implications. Lab on a Chip 7, 299–301.Google ScholarPubMed
Engmann, J., Servais, C. & Burbidge, A. S. 2005 Squeeze flow theory and applications to rheometry: a review. J. Non-Newtonian Fluid Mech. 132, 1–27.CrossRefGoogle Scholar
Goldman, A. J., Cox, R. G. & Brenner, H. 1967 Slow viscous motion of a sphere parallel to a plane wall – II. Couette flow. Chem. Engng Sci. 22, 653–660.CrossRefGoogle Scholar
Goren, S. L. & O’Neill, M. E. 1971 On the hydrodynamic resistance to a particle of a dilute suspension when in the neighbourhood of a large obstacle. Chem. Engng Sci. 26, 325–338.CrossRefGoogle Scholar
Henry, C. L. & Craig, V. S. J. 2009 Measurement of no-slip and slip boundary conditions in confined Newtonian fluids using atomic force microscopy. Phys. Chem. Chem. Phys. 11, 9514–9521.CrossRefGoogle ScholarPubMed
Hollingsworth, A. D. & Silebi, C. A. 1996 Electrokinetic lift effects observed in the transport of submicrometer particles through microcapillary tubes. Langmuir 12, 613–623.CrossRefGoogle Scholar
Honig, C. D. F. & Ducker, W. A. 2007 No-slip hydrodynamic boundary condition for hydrophilic particles. Phys. Rev. Lett. 98, 028305.CrossRefGoogle ScholarPubMed
Hu, X., Nanney, W., Umeda, K., Ye, T. & Martini, A. 2018 Combined experimental and simulation study of amplitude modulation atomic force microscopy measurements of self-assembled monolayers in water. Langmuir 34, 9627–9633.CrossRefGoogle ScholarPubMed
Israelachvili, J. N. 1986 Measurement of the viscosity of liquids in very thin films. J. Colloid Interface Sci. 110, 263–271.CrossRefGoogle Scholar
Israelachvili, J. N. 2011 Intermolecular and Surface Forces, 3rd edn. Academic Press.Google Scholar
Laanait, N., Mihaylov, M., Hou, B. et al. 2012 Tuning ion correlations at an electrified soft interface. Proc. Natl Acad. Sci. USA 109, 20326–20331.CrossRefGoogle ScholarPubMed
Labuda, A., Kobayashi, K., Kiracofe, D., Suzuki, K., Grütter, P. H. & Yamada, H. 2011 Comparison of photothermal and piezoacoustic excitation methods for frequency and phase modulation atomic force microscopy in liquid environments. AIP Adv. 1, 022136.CrossRefGoogle Scholar
Levine, S. & Bell, G. M. 1960 Theory of a modified Poisson–Boltzmann equation. I. The volume effect of hydrdated ions. J. Phys. Chem. 64, 1188–1195.CrossRefGoogle Scholar
Levine, S., Marriott, J. R., Neale, G. & Epstein, N. 1975 Theory of electrokinetic flow in fine cylindrical capillaries at high zeta-potentials. J. Colloid Interface Sci. 52, 136–149.CrossRefGoogle Scholar
Levy, A., Andelman, D. & Orland, H. 2012 Dielectric constant of ionic solutions: a field-theory approach. Phys. Rev. Lett. 108, 227801.CrossRefGoogle ScholarPubMed
Li, D. 2001 Electro-viscous effects on pressure-driven liquid flow in microchannels. Colloids Surf. A 195, 35–57.CrossRefGoogle Scholar
Li, D. 2008 Encyclopedia of Microfluidics and Nanofluidics. Springer US.CrossRefGoogle Scholar
Liu, F., Klaassen, A., Zhao, C., Mugele, F. & van den Ende, D. 2018 Electroviscous dissipation in aqueous electrolyte films with overlapping electric double layers. J. Phys. Chem. B 122, 933–946.CrossRefGoogle ScholarPubMed
Liu, F., Zhao, C., Mugele, F. & Ende, D. v. d. 2015 Amplitude modulation atomic force microscopy, is acoustic driving in liquid quantitatively reliable? Nanotechnology 26, 385703.CrossRefGoogle ScholarPubMed
Manev, E. D. & Nguyen, A. V. 2005 Critical thickness of microscopic thin liquid films. Adv. Colloid Interface Sci. 114–115, 133–146.CrossRefGoogle ScholarPubMed
Masliyah, J. H. & Bhattacharjee, S. 2006 Electrokinetic and Colloid Transport Phenomena. Wiley.CrossRefGoogle Scholar
McNamee, C. E. 2019 Effect of a liquid flow on the forces between charged solid surfaces and the non-equilibrium electric double layer. Adv. Colloid Interface Sci. 266, 21–33.CrossRefGoogle ScholarPubMed
Montes Ruiz-Cabello, F. J., Trefalt, G., Maroni, P. & Borkovec, M. 2014 Electric double-layer potentials and surface regulation properties measured by colloidal-probe atomic force microscopy. Phys. Rev. E 90, 012301.Google ScholarPubMed
Muller, V. M. 1990 Electroviscous effect when charged surfaces approach one another in electrolyte solutions. J. Colloid Interface Sci. 136, 61–67.CrossRefGoogle Scholar
O’Shea, S. J. & Welland, M. E. 1998 Atomic force microscopy at solid–liquid interfaces. Langmuir 14, 4186–4197.CrossRefGoogle Scholar
Peters, P. B., van Roij, R., Bazant, M. Z. & Biesheuvel, P. M. 2016 Analysis of electrolyte transport through charged nanopores. Phys. Rev. E 93, 053108.Google ScholarPubMed
Probstein, R. F. 1994 Physicochemical Hydrodynamics: An Introduction. Wiley.CrossRefGoogle Scholar
Qiao, R. & Aluru, N. R. 2005 Scaling of electrokinetic transport in nanometer channels. Langmuir 21, 8972–8977.CrossRefGoogle ScholarPubMed
Raviv, U., Laurat, P. & Klein, J. 2001 Fluidity of water confined to subnanometre films. Nature 413, 51–54.CrossRefGoogle ScholarPubMed
Raviv, U., Perkin, S., Laurat, P. & Klein, J. 2004 Fluidity of water confined down to subnanometer films. Langmuir 20, 5322–5332.CrossRefGoogle ScholarPubMed
Ren, C. L. & Li, D. 2004 Electroviscous effects on pressure-driven flow of dilute electrolyte solutions in small microchannels. J. Colloid Interface Sci. 274, 319–330.CrossRefGoogle ScholarPubMed
Revil, A. & Glover, P. W. J. 1997 Theory of ionic-surface electrical conduction in porous media. Phys. Rev. B 55, 1757–1773.CrossRefGoogle Scholar
Rice, C. L. & Whitehead, R. 1965 Electrokinetic flow in a narrow cylindrical capillary. J. Phys. Chem. 69, 4017–4024.CrossRefGoogle Scholar
Russel, W. B., Saville, D. A. & Schowalter, W. R. 1989 Colloidal Dispersions. Cambridge University Press.CrossRefGoogle Scholar
Schnitzer, O., Frankel, I. & Yariv, E. 2012 Streaming-potential phenomena in the thin-Debye-layer limit. Part 2. Moderate Péclet numbers. J. Fluid Mech. 704, 109–136.CrossRefGoogle Scholar
Stone, H. A. 2005 On lubrication flows in geometries with zero local curvature. Chem. Engng Sci. 60, 4838–4845.CrossRefGoogle Scholar
Striegel, A. M. & Brewer, A. K. 2012 Hydrodynamic chromatography. Annu. Rev. Anal. Chem. 5, 15–34.CrossRefGoogle ScholarPubMed
Tabatabaei, S. M. & van de Ven, T. G. M. 2010 Tangential electroviscous drag on a sphere surrounded by a thin double layer near a wall for arbitrary particle–wall separations. J. Fluid Mech. 656, 360–406.CrossRefGoogle Scholar
Talapatra, S. & Chakraborty, S. 2009 Squeeze-flow electroosmotic pumping between charged parallel plates. Intl J. Fluid Mech. Res. 36, 460–472.CrossRefGoogle Scholar
Tambe, D. E. & Sharma, M. M. 1994 The effect of colloidal particles on fluid–fluid interfacial properties and emulsion stability. Adv. Colloid Interface Sci. 52, 1–63.CrossRefGoogle Scholar
Valkovska, D. S. & Danov, K. D. 2001 Influence of ionic surfactants on the drainage velocity of thin liquid films. J. Colloid Interface Sci. 241, 400–412.CrossRefGoogle Scholar
van de Ven, T. G. M. 1989 Colloidal Hydrodynamics. Academic Press.Google Scholar
van de Ven, T. G. M., Warszyski, P. & Dukhin, S. S. 1993 Electrokinetic lift of small particles. J. Colloid Interface Sci. 157, 328–331.CrossRefGoogle Scholar
Vinogradova, O. I. & Yakubov, G. E. 2003 Dynamic effects on force measurements. 2. Lubrication and the atomic force microscope. Langmuir 19, 1227–1234.CrossRefGoogle Scholar
Warszyski, P. 2000 Coupling of hydrodynamic and electric interactions in adsorption of colloidal particles. Adv. Colloid Interface Sci. 84, 47–142.CrossRefGoogle Scholar
Warszyski, P. & van de Ven, T. G. M. 1990 Electroviscous forces. Faraday Discuss. Chem. Soc. 90, 313–321.CrossRefGoogle Scholar
Warszyski, P. & van de Ven, T. G. M. 1991 Effect of electroviscous drag on the coagulation and deposition of electrically charged colloidal particles. Adv. Colloid Interface Sci. 36, 33–63.CrossRefGoogle Scholar
Warszyski, P. & van de Ven, T. G. M. 2000 Electroviscous forces on a charged cylinder moving near a charged wall. J. Colloid Interface Sci. 223, 1–15.CrossRefGoogle Scholar
Warszyski, P., Wu, X. & van de Ven, T. G. M. 1998 Electrokinetic lift force for a charged particle moving near a charged wall – a modified theory and experiment. Colloids Surf. A 140, 183–198.CrossRefGoogle Scholar
Wu, X., Warszyski, P. & van de Ven, T. G. M. 1996 Electrokinetic lift: observations and comparisons with theories. J. Colloid Interface Sci. 180, 61–69.CrossRefGoogle Scholar
Yariv, E., Schnitzer, O. & Frankel, I. 2011 Streaming-potential phenomena in the thin-Debye-layer limit. Part 1. General theory. J. Fluid Mech. 685, 306–334.CrossRefGoogle Scholar
Zhang, W., Wang, Q., Zeng, M. & Zhao, C. 2019 Thermoelectric effect and temperature-gradient-driven electrokinetic flow of electrolyte solutions in charged nanocapillaries. Intl J. Heat Mass Transfer 143, 118569.CrossRefGoogle Scholar
Zhao, C., Ebeling, D., Siretanu, I., van den Ende, D. & Mugele, F. 2015 Extracting local surface charges and charge regulation behavior from atomic force microscopy measurements at heterogeneous solid-electrolyte interfaces. Nanoscale 7, 16298–16311.CrossRefGoogle ScholarPubMed
Zhao, H. & Zhai, S. 2013 The influence of dielectric decrement on electrokinetics. J. Fluid Mech. 724, 69–94.CrossRefGoogle ScholarPubMed