Published online by Cambridge University Press: 13 December 2013
The basic dynamics of a prolate spheroidal particle suspended in shear flow is studied using lattice Boltzmann simulations. The spheroid motion is determined by the particle Reynolds number (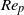 ${\mathit{Re}}_{p} $) and Stokes number (
${\mathit{Re}}_{p} $) and Stokes number (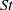 $\mathit{St}$), estimating the effects of fluid and particle inertia, respectively, compared with viscous forces on the particle. The particle Reynolds number is defined by
$\mathit{St}$), estimating the effects of fluid and particle inertia, respectively, compared with viscous forces on the particle. The particle Reynolds number is defined by 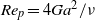 ${\mathit{Re}}_{p} = 4G{a}^{2} / \nu $, where
${\mathit{Re}}_{p} = 4G{a}^{2} / \nu $, where 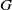 $G$ is the shear rate,
$G$ is the shear rate,  $a$ is the length of the spheroid major semi-axis and
$a$ is the length of the spheroid major semi-axis and  $\nu $ is the kinematic viscosity. The Stokes number is defined as
$\nu $ is the kinematic viscosity. The Stokes number is defined as 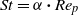 $\mathit{St}= \alpha \boldsymbol{\cdot} {\mathit{Re}}_{p} $, where
$\mathit{St}= \alpha \boldsymbol{\cdot} {\mathit{Re}}_{p} $, where  $\alpha $ is the solid-to-fluid density ratio. Here, a neutrally buoyant prolate spheroidal particle (
$\alpha $ is the solid-to-fluid density ratio. Here, a neutrally buoyant prolate spheroidal particle (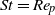 $\mathit{St}= {\mathit{Re}}_{p} $) of aspect ratio (major axis/minor axis)
$\mathit{St}= {\mathit{Re}}_{p} $) of aspect ratio (major axis/minor axis) 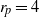 ${r}_{p} = 4$ is considered. The long-term rotational motion for different initial orientations and
${r}_{p} = 4$ is considered. The long-term rotational motion for different initial orientations and 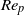 ${\mathit{Re}}_{p} $ is explained by the dominant inertial effect on the particle. The transitions between rotational states are subsequently studied in detail in terms of nonlinear dynamics. Fluid inertia is seen to cause several bifurcations typical for a nonlinear system with odd symmetry around a double zero eigenvalue. Particle inertia gives rise to centrifugal forces which drives the particle to rotate with the symmetry axis in the flow-gradient plane (tumbling). At high
${\mathit{Re}}_{p} $ is explained by the dominant inertial effect on the particle. The transitions between rotational states are subsequently studied in detail in terms of nonlinear dynamics. Fluid inertia is seen to cause several bifurcations typical for a nonlinear system with odd symmetry around a double zero eigenvalue. Particle inertia gives rise to centrifugal forces which drives the particle to rotate with the symmetry axis in the flow-gradient plane (tumbling). At high 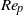 ${\mathit{Re}}_{p} $, the motion is constrained to this planar motion regardless of initial orientation. At a certain critical Reynolds number,
${\mathit{Re}}_{p} $, the motion is constrained to this planar motion regardless of initial orientation. At a certain critical Reynolds number, 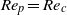 ${\mathit{Re}}_{p} = {\mathit{Re}}_{c} $, a motionless (steady) state is created through an infinite-period saddle-node bifurcation and consequently the tumbling period near the transition is scaled as
${\mathit{Re}}_{p} = {\mathit{Re}}_{c} $, a motionless (steady) state is created through an infinite-period saddle-node bifurcation and consequently the tumbling period near the transition is scaled as 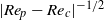 $\vert {\mathit{Re}}_{p} - {\mathit{Re}}_{c} {\vert }^{- 1/ 2} $. Analyses in this paper show that if a transition from tumbling to steady state occurs at
$\vert {\mathit{Re}}_{p} - {\mathit{Re}}_{c} {\vert }^{- 1/ 2} $. Analyses in this paper show that if a transition from tumbling to steady state occurs at 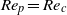 ${\mathit{Re}}_{p} = {\mathit{Re}}_{c} $, then any parameter
${\mathit{Re}}_{p} = {\mathit{Re}}_{c} $, then any parameter 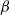 $\beta $ (e.g. confinement or particle spacing) that influences the value of
$\beta $ (e.g. confinement or particle spacing) that influences the value of 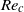 ${\mathit{Re}}_{c} $, such that
${\mathit{Re}}_{c} $, such that 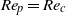 ${\mathit{Re}}_{p} = {\mathit{Re}}_{c} $ as
${\mathit{Re}}_{p} = {\mathit{Re}}_{c} $ as 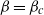 $\beta = {\beta }_{c} $, will lead to a period that scales as
$\beta = {\beta }_{c} $, will lead to a period that scales as  $\vert \beta - {\beta }_{c} {\vert }^{- 1/ 2} $ and is independent of particle shape or any geometric aspect ratio in the flow.
$\vert \beta - {\beta }_{c} {\vert }^{- 1/ 2} $ and is independent of particle shape or any geometric aspect ratio in the flow.