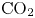1. Introduction
Geological storage of ![]() ${\rm CO}_2$ has been identified as a key technology in the global effort to reduce greenhouse gas emissions and mitigate the adverse effects of climate change (IPCC 2014). However, there remain considerable technical challenges for
${\rm CO}_2$ has been identified as a key technology in the global effort to reduce greenhouse gas emissions and mitigate the adverse effects of climate change (IPCC 2014). However, there remain considerable technical challenges for ![]() ${\rm CO}_2$ storage, and in particular the development of strategies for maximising the fraction of the pore space in a reservoir in which
${\rm CO}_2$ storage, and in particular the development of strategies for maximising the fraction of the pore space in a reservoir in which ![]() ${\rm CO}_2$ can be stored. The challenge of accessing all the pore space in a given reservoir is related to several factors including the low viscosity of the
${\rm CO}_2$ can be stored. The challenge of accessing all the pore space in a given reservoir is related to several factors including the low viscosity of the ![]() ${\rm CO}_2$, which can lead to viscous fingering of
${\rm CO}_2$, which can lead to viscous fingering of ![]() ${\rm CO}_2$ through the formation water (Saffman & Taylor Reference Saffman and Taylor1958); the buoyancy of the
${\rm CO}_2$ through the formation water (Saffman & Taylor Reference Saffman and Taylor1958); the buoyancy of the ![]() ${\rm CO}_2$, which can lead to
${\rm CO}_2$, which can lead to ![]() ${\rm CO}_2$ rising to the upper boundary of the reservoir, below the seal rock, bypassing the rock lower in the formation (Huppert & Woods Reference Huppert and Woods1995; Neufeld et al. Reference Neufeld2010; Nordbotten & Celia Reference Nordbotten and Celia2012) and heterogeneities in the rock structure that can lead to
${\rm CO}_2$ rising to the upper boundary of the reservoir, below the seal rock, bypassing the rock lower in the formation (Huppert & Woods Reference Huppert and Woods1995; Neufeld et al. Reference Neufeld2010; Nordbotten & Celia Reference Nordbotten and Celia2012) and heterogeneities in the rock structure that can lead to ![]() ${\rm CO}_2$ migrating along the high permeability pathways through the formation, bypassing much of the rock (Woods Reference Woods2015; Hinton & Woods Reference Hinton and Woods2018).
${\rm CO}_2$ migrating along the high permeability pathways through the formation, bypassing much of the rock (Woods Reference Woods2015; Hinton & Woods Reference Hinton and Woods2018).
In addition to these general effects, the mechanisms of trapping of the ![]() ${\rm CO}_2$ in the formation are key for assessing the storage capacity of a reservoir and the fraction of the storage capacity that can be accessed by a particular injection strategy. The main mechanisms of trapping include (i) structural trapping, wherein the geometry of the subsurface system has localised high points where the buoyant
${\rm CO}_2$ in the formation are key for assessing the storage capacity of a reservoir and the fraction of the storage capacity that can be accessed by a particular injection strategy. The main mechanisms of trapping include (i) structural trapping, wherein the geometry of the subsurface system has localised high points where the buoyant ![]() ${\rm CO}_2$ is trapped; (ii) capillary trapping, whereby a cloud of residually trapped
${\rm CO}_2$ is trapped; (ii) capillary trapping, whereby a cloud of residually trapped ![]() ${\rm CO}_2$ accumulates in the pore spaces of the rocks behind an advancing water-
${\rm CO}_2$ accumulates in the pore spaces of the rocks behind an advancing water-![]() ${\rm CO}_2$ displacement front; (iii) dissolution trapping, whereby the
${\rm CO}_2$ displacement front; (iii) dissolution trapping, whereby the ![]() ${\rm CO}_2$ dissolves into any undersaturated formation water and, ultimately, (iv) mineralisation of the
${\rm CO}_2$ dissolves into any undersaturated formation water and, ultimately, (iv) mineralisation of the ![]() ${\rm CO}_2$ (Hermanrud et al. Reference Hermanrud, Andresen, Eiken, Hansen, Janbu, Lippard, Bolås, Simmenes, Teige and Østmo2009).
${\rm CO}_2$ (Hermanrud et al. Reference Hermanrud, Andresen, Eiken, Hansen, Janbu, Lippard, Bolås, Simmenes, Teige and Østmo2009).
In the present paper we focus on the storage of ![]() ${\rm CO}_2$ in anticline-type structures, with a natural trap for
${\rm CO}_2$ in anticline-type structures, with a natural trap for ![]() ${\rm CO}_2$ at the top of the structure where it can collect above the formation water below the top seal of the system. Figure 1(a,b) is adapted from Chadwick et al. (Reference Chadwick, Arts, Bernstone, May, Thibeau and Zweigel2008) and shows an illustration of the Schweinrich storage structure in Germany. This is a typical example of a layered formation, with two primary storage layers, separated by low permeability claystone. The anticline is an elongate three-dimensional structure, and the section through the narrow width of the structure illustrates the variation in the depth of the spill point on each side of the structure. Such structural traps are ideal locations for carbon storage, and there is much interest in such sites. The diagram displays a cross-section of the structural trap that is part of an extensive aquifer indicated by the red dashed line along the plan view of figure 1(a). The surrounding formation extends laterally from the trap and the capacity of the structural trap is given by the volume of
${\rm CO}_2$ at the top of the structure where it can collect above the formation water below the top seal of the system. Figure 1(a,b) is adapted from Chadwick et al. (Reference Chadwick, Arts, Bernstone, May, Thibeau and Zweigel2008) and shows an illustration of the Schweinrich storage structure in Germany. This is a typical example of a layered formation, with two primary storage layers, separated by low permeability claystone. The anticline is an elongate three-dimensional structure, and the section through the narrow width of the structure illustrates the variation in the depth of the spill point on each side of the structure. Such structural traps are ideal locations for carbon storage, and there is much interest in such sites. The diagram displays a cross-section of the structural trap that is part of an extensive aquifer indicated by the red dashed line along the plan view of figure 1(a). The surrounding formation extends laterally from the trap and the capacity of the structural trap is given by the volume of ![]() ${\rm CO}_2$ that can be retained in the trap structure, for example, through buoyancy forces, without spreading laterally into the extensive connected aquifer. Developing a strategy to inject
${\rm CO}_2$ that can be retained in the trap structure, for example, through buoyancy forces, without spreading laterally into the extensive connected aquifer. Developing a strategy to inject ![]() ${\rm CO}_2$ to reach this maximum storage capacity is challenging, and this overarching question motivates the present work.
${\rm CO}_2$ to reach this maximum storage capacity is challenging, and this overarching question motivates the present work.

Figure 1. (a) The plan view shows contours of elevation below sea level from the Schweinrich anticline structure in Germany – adapted from Chadwick et al. (Reference Chadwick, Arts, Bernstone, May, Thibeau and Zweigel2008). In the cross-sectional diagram we consider a cross-section taken from north west to south east, indicated by the red dashed line. The simplified illustration of the anticline shows two light brown layers that represent high permeability storage rock separated by an intermediate mudstone layer that is coloured a darker brown here. The structure also shows two spill points, which are the maximum depths at which the structure can retain ![]() ${\rm CO}_2$. (b) Cartoon showing injection of
${\rm CO}_2$. (b) Cartoon showing injection of ![]() ${\rm CO}_2$ (green) into the lower layer of a two layered formation. We see a pool of
${\rm CO}_2$ (green) into the lower layer of a two layered formation. We see a pool of ![]() ${\rm CO}_2$ begin to form beneath the mudstone separating the two layers. At some time during injection
${\rm CO}_2$ begin to form beneath the mudstone separating the two layers. At some time during injection ![]() ${\rm CO}_2$ may pass through the mudstone and into the upper layer. Eventually the depth of
${\rm CO}_2$ may pass through the mudstone and into the upper layer. Eventually the depth of ![]() ${\rm CO}_2$ in one of the layers will reach the spill point and
${\rm CO}_2$ in one of the layers will reach the spill point and ![]() ${\rm CO}_2$ will spill into the neighbouring aquifer.
${\rm CO}_2$ will spill into the neighbouring aquifer.
To explore the fraction of the storage capacity accessible to the injection fluid, in principle we need to calculate the flow path of the ![]() ${\rm CO}_2$ from the injection wells, up through the formation to the point of accumulation below the seal. However, many formations are heterogeneous and involve internal baffles and regions of different permeability, leading to very tortuous pathways for the
${\rm CO}_2$ from the injection wells, up through the formation to the point of accumulation below the seal. However, many formations are heterogeneous and involve internal baffles and regions of different permeability, leading to very tortuous pathways for the ![]() ${\rm CO}_2$ through the formation (Hesse & Woods Reference Hesse and Woods2010) and the formation of long wakes of residually trapped
${\rm CO}_2$ through the formation (Hesse & Woods Reference Hesse and Woods2010) and the formation of long wakes of residually trapped ![]() ${\rm CO}_2$ (Hesse, Orr & Tchelepi Reference Hesse, Orr and Tchelepi2008; Hinton & Woods Reference Hinton and Woods2021). Furthermore, the geological strata often includes multiple continuous layers of permeable rock, separated by thin layers of low permeability mudstone, often with a capillary entry pressure for the
${\rm CO}_2$ (Hesse, Orr & Tchelepi Reference Hesse, Orr and Tchelepi2008; Hinton & Woods Reference Hinton and Woods2021). Furthermore, the geological strata often includes multiple continuous layers of permeable rock, separated by thin layers of low permeability mudstone, often with a capillary entry pressure for the ![]() ${\rm CO}_2$. These can direct a
${\rm CO}_2$. These can direct a ![]() ${\rm CO}_2$ plume upwards along a small fraction of the formation, leading to secondary pools of trapped
${\rm CO}_2$ plume upwards along a small fraction of the formation, leading to secondary pools of trapped ![]() ${\rm CO}_2$ below each of the mudstone layers (Chadwick et al. Reference Chadwick, Arts, Eiken, Kirby, Lindeberg and Zweigel2004; Cavanagh & Haszeldine Reference Cavanagh and Haszeldine2014; Onoja & Shariatipour Reference Onoja and Shariatipour2019) and complex flow patterns.
${\rm CO}_2$ below each of the mudstone layers (Chadwick et al. Reference Chadwick, Arts, Eiken, Kirby, Lindeberg and Zweigel2004; Cavanagh & Haszeldine Reference Cavanagh and Haszeldine2014; Onoja & Shariatipour Reference Onoja and Shariatipour2019) and complex flow patterns.
The capillary entry pressure of intermediate mudstones may also prevent migration of ![]() ${\rm CO}_2$ between storage layers. In the Schweinrich structure the two main reservoir layers are separated by a layer of claystone that is at least 10 m thick throughout the lateral extent of the structure. Core sampling has shown that the capillary entry pressure of the claystone layer is likely greater than 4 MPa, which is equivalent to a
${\rm CO}_2$ between storage layers. In the Schweinrich structure the two main reservoir layers are separated by a layer of claystone that is at least 10 m thick throughout the lateral extent of the structure. Core sampling has shown that the capillary entry pressure of the claystone layer is likely greater than 4 MPa, which is equivalent to a ![]() ${\rm CO}_2$ column of around 700 m under hydrostatic conditions (Chadwick et al. Reference Chadwick, Arts, Bernstone, May, Thibeau and Zweigel2008). This suggests that in this system the
${\rm CO}_2$ column of around 700 m under hydrostatic conditions (Chadwick et al. Reference Chadwick, Arts, Bernstone, May, Thibeau and Zweigel2008). This suggests that in this system the ![]() ${\rm CO}_2$ would not flow from the lower to the upper formation and the two layers can be considered to be independent of each other.
${\rm CO}_2$ would not flow from the lower to the upper formation and the two layers can be considered to be independent of each other.
There are, however, examples of storage sites where there is significant connectivity between layers. The Utsira formation at the Sleipner storage site, Norway, has been a site of ![]() ${\rm CO}_2$ injection since 1994 (Chadwick et al. Reference Chadwick2010; Cavanagh & Haszeldine Reference Cavanagh and Haszeldine2014; Onoja & Shariatipour Reference Onoja and Shariatipour2019). Sleipner comprises nine primary storage layers separated by thin layers of low permeability shale.
${\rm CO}_2$ injection since 1994 (Chadwick et al. Reference Chadwick2010; Cavanagh & Haszeldine Reference Cavanagh and Haszeldine2014; Onoja & Shariatipour Reference Onoja and Shariatipour2019). Sleipner comprises nine primary storage layers separated by thin layers of low permeability shale.
Sleipner is an example of a layered formation where there is a significant flux of ![]() ${\rm CO}_2$ through the intermediate shale barriers. Core sampling of the shale barriers indicates a capillary entry pressure range between 1.6–1.9 MPa. This would require
${\rm CO}_2$ through the intermediate shale barriers. Core sampling of the shale barriers indicates a capillary entry pressure range between 1.6–1.9 MPa. This would require ![]() ${\rm CO}_2$ column heights of hundreds of metres, whereas the observed column heights at Sleipner are less than 20 m. Cavanagh & Haszeldine (Reference Cavanagh and Haszeldine2014) proposed that there could be significant micro-fracturing throughout the shale barriers resulting in an effective capillary entry pressure of around 50 kPa. This brings into focus the challenge of characterising intermediate low permeability layers and the connectivity of storage layers.
${\rm CO}_2$ column heights of hundreds of metres, whereas the observed column heights at Sleipner are less than 20 m. Cavanagh & Haszeldine (Reference Cavanagh and Haszeldine2014) proposed that there could be significant micro-fracturing throughout the shale barriers resulting in an effective capillary entry pressure of around 50 kPa. This brings into focus the challenge of characterising intermediate low permeability layers and the connectivity of storage layers.
In addition to the flow path of the ![]() ${\rm CO}_2$, there may also be a limit on the injection pressure and, hence, flow rate owing to the need to prevent damage to the seal rock (Bai et al. Reference Bai, Li, Wu, Wang and Liu2017; Bohloli et al. Reference Bohloli, Ringrose, Grande and Nazarian2017). This may change the balance between the pressure at the injection well and the buoyancy force driving the flow through the system, with the increased role of the buoyancy forces accelerating the ascent of the
${\rm CO}_2$, there may also be a limit on the injection pressure and, hence, flow rate owing to the need to prevent damage to the seal rock (Bai et al. Reference Bai, Li, Wu, Wang and Liu2017; Bohloli et al. Reference Bohloli, Ringrose, Grande and Nazarian2017). This may change the balance between the pressure at the injection well and the buoyancy force driving the flow through the system, with the increased role of the buoyancy forces accelerating the ascent of the ![]() ${\rm CO}_2$ through the formation. In a given system, the configuration of the injection wells will also have an important role in determining how the injected
${\rm CO}_2$ through the formation. In a given system, the configuration of the injection wells will also have an important role in determining how the injected ![]() ${\rm CO}_2$ spreads through the system (Luboń Reference Luboń2021).
${\rm CO}_2$ spreads through the system (Luboń Reference Luboń2021).
Given these complexities that impact the injection and migration of ![]() ${\rm CO}_2$ through a reservoir, we have chosen to focus on an idealised problem in which we explore the dynamics of
${\rm CO}_2$ through a reservoir, we have chosen to focus on an idealised problem in which we explore the dynamics of ![]() ${\rm CO}_2$ injection into a layered anticline structure. Motivated by the example of
${\rm CO}_2$ injection into a layered anticline structure. Motivated by the example of ![]() ${\rm CO}_2$ injection into the Utsira formation of the Sleipner reservoir, we model the injection through a well near the base of the formation (figure 1b). We assume that there is a series of spatially continuous low permeability mudstone layers, of permeability
${\rm CO}_2$ injection into the Utsira formation of the Sleipner reservoir, we model the injection through a well near the base of the formation (figure 1b). We assume that there is a series of spatially continuous low permeability mudstone layers, of permeability ![]() $k_m$, between the more permeable reservoir layers of permeability
$k_m$, between the more permeable reservoir layers of permeability ![]() $k_a$, and that the pressure drop associated with the
$k_a$, and that the pressure drop associated with the ![]() ${\rm CO}_2$ flow across these mudstone layers represents the main loss of pressure as the
${\rm CO}_2$ flow across these mudstone layers represents the main loss of pressure as the ![]() ${\rm CO}_2$ rises to the top of the formation. With a mudstone thickness
${\rm CO}_2$ rises to the top of the formation. With a mudstone thickness ![]() $b_m$, the pressure drop for a flow rate
$b_m$, the pressure drop for a flow rate ![]() $u_m$ per unit area is
$u_m$ per unit area is
where ![]() $\mu _c$ is the viscosity of the
$\mu _c$ is the viscosity of the ![]() ${\rm CO}_2$. The pressure drop for a comparable flow in the main aquifer layers of permeability
${\rm CO}_2$. The pressure drop for a comparable flow in the main aquifer layers of permeability ![]() $k_a$ and thickness
$k_a$ and thickness ![]() $H$ is
$H$ is
Provided that
and the simplification applies. For ![]() $H \sim 1\unicode{x2013}10$ m and
$H \sim 1\unicode{x2013}10$ m and ![]() $b_m \sim 0.01\unicode{x2013}0.1$ m, we require that
$b_m \sim 0.01\unicode{x2013}0.1$ m, we require that ![]() $k_m<0.01k_a$, which would represent a very permeable mudstone layer if
$k_m<0.01k_a$, which would represent a very permeable mudstone layer if ![]() $k_a$ is of order
$k_a$ is of order ![]() $10^{-12}$ to
$10^{-12}$ to ![]() $10^{-14}$ m
$10^{-14}$ m![]() $^2$ (Armitage et al. Reference Armitage, Worden, Faulkner, Butcher and Espie2016).
$^2$ (Armitage et al. Reference Armitage, Worden, Faulkner, Butcher and Espie2016).
In addition to this constraint, we also assume that the injection pressure is small compared with the difference in hydrostatic pressure between the ![]() ${\rm CO}_2$ and saline formation fluid across each of the layers in the formation so that the local dynamics is driven by the buoyancy forces. The injection pressure may be estimated in terms of the radial spreading of a cloud of
${\rm CO}_2$ and saline formation fluid across each of the layers in the formation so that the local dynamics is driven by the buoyancy forces. The injection pressure may be estimated in terms of the radial spreading of a cloud of ![]() ${\rm CO}_2$ from the injection well of radius
${\rm CO}_2$ from the injection well of radius ![]() $r_w$ to the larger radius
$r_w$ to the larger radius ![]() $r$, which leads to the result from Darcy's law that the pressure drop scales as
$r$, which leads to the result from Darcy's law that the pressure drop scales as
where ![]() $Q$ is the injection flux. In order for the buoyancy forces to dominate the motion we require that
$Q$ is the injection flux. In order for the buoyancy forces to dominate the motion we require that
where ![]() $\Delta \rho$ is the density difference between the brine and the
$\Delta \rho$ is the density difference between the brine and the ![]() ${\rm CO}_2$ plume, and this imposes a constraint on the injection rate for a given formation permeability and scale of the flow,
${\rm CO}_2$ plume, and this imposes a constraint on the injection rate for a given formation permeability and scale of the flow, ![]() $r$. With higher injection rates or lower permeability formations we need to account for the dynamic pressure associated with the
$r$. With higher injection rates or lower permeability formations we need to account for the dynamic pressure associated with the ![]() ${\rm CO}_2$ motion from the injection well into the crest of the anticline. However, in order to focus on the balance of the injection rate and the buoyancy flux across each mudstone layer, in this paper we develop our models in the limit of (1.5), corresponding to a permeable aquifer. A more general numerical model would be required for a lower permeability system (e.g. Chadwick et al. Reference Chadwick, Arts, Bernstone, May, Thibeau and Zweigel2008). Finally, we assume that there is a finite capillary entry pressure associated with the mudstone layers. This leads to the formation of pools of
${\rm CO}_2$ motion from the injection well into the crest of the anticline. However, in order to focus on the balance of the injection rate and the buoyancy flux across each mudstone layer, in this paper we develop our models in the limit of (1.5), corresponding to a permeable aquifer. A more general numerical model would be required for a lower permeability system (e.g. Chadwick et al. Reference Chadwick, Arts, Bernstone, May, Thibeau and Zweigel2008). Finally, we assume that there is a finite capillary entry pressure associated with the mudstone layers. This leads to the formation of pools of ![]() ${\rm CO}_2$ in each layer, and we show that this can have a material impact on the overall volume of
${\rm CO}_2$ in each layer, and we show that this can have a material impact on the overall volume of ![]() ${\rm CO}_2$ trapped in the system.
${\rm CO}_2$ trapped in the system.
In developing the model, the focus is on the dynamics of filling the reservoir, whereby the ![]() ${\rm CO}_2$ migrates from the base of the system upwards through the mudstone layers leading to the formation of a series of pools of
${\rm CO}_2$ migrates from the base of the system upwards through the mudstone layers leading to the formation of a series of pools of ![]() ${\rm CO}_2$, until one fills sufficiently that if the injection were to continue,
${\rm CO}_2$, until one fills sufficiently that if the injection were to continue, ![]() ${\rm CO}_2$ would flow out laterally into the neighbouring aquifer. We start the paper by describing the geometry of the idealised anticline, from which we can estimate the maximum storage capacity of
${\rm CO}_2$ would flow out laterally into the neighbouring aquifer. We start the paper by describing the geometry of the idealised anticline, from which we can estimate the maximum storage capacity of ![]() ${\rm CO}_2$. We then build in the dynamics of the injection, modelling the time-dependent migration of
${\rm CO}_2$. We then build in the dynamics of the injection, modelling the time-dependent migration of ![]() ${\rm CO}_2$ through the system. Finally, we consider whether there is any continued migration of
${\rm CO}_2$ through the system. Finally, we consider whether there is any continued migration of ![]() ${\rm CO}_2$ following the end of the injection process, and illustrate how this imposes further constraints on the injection volume. We then present a simple analogue laboratory experiment that illustrates some of the features of the model.
${\rm CO}_2$ following the end of the injection process, and illustrate how this imposes further constraints on the injection volume. We then present a simple analogue laboratory experiment that illustrates some of the features of the model.
2. Model geometry and static controls on storage
For the main part of the paper, we assume that the anticline is a long fold-like structure as in the Schwienrich formation, consisting of two high permeability layers of equal thickness, ![]() $H$, each of which is symmetrical about the crest of the anticline, and each of which connects with a horizontal aquifer (figure 1b). We consider the idealised case in which the
$H$, each of which is symmetrical about the crest of the anticline, and each of which connects with a horizontal aquifer (figure 1b). We consider the idealised case in which the ![]() ${\rm CO}_2$ is injected into a series of long horizontal wells that are parallel to the long axis of the anticline in the lower layer of the system. This leads to an effectively two-dimensional flow problem with
${\rm CO}_2$ is injected into a series of long horizontal wells that are parallel to the long axis of the anticline in the lower layer of the system. This leads to an effectively two-dimensional flow problem with ![]() ${\rm CO}_2$ initially accumulating in the crest of the lower layer, and eventually some
${\rm CO}_2$ initially accumulating in the crest of the lower layer, and eventually some ![]() ${\rm CO}_2$ may then drain into the upper layer. In practice there will be some end effects in the third dimension but the present two-dimensional problem provides a useful simplification for exploring some of the controls on the filling of the system. In Appendix A we briefly discuss the case of an axisymmetric anticline, for which the geometry and, hence, quantitative details are different, but we show that the principles identified for the two-dimensional model carry over.
${\rm CO}_2$ may then drain into the upper layer. In practice there will be some end effects in the third dimension but the present two-dimensional problem provides a useful simplification for exploring some of the controls on the filling of the system. In Appendix A we briefly discuss the case of an axisymmetric anticline, for which the geometry and, hence, quantitative details are different, but we show that the principles identified for the two-dimensional model carry over.
2.1. Geometry of the anticline system
The height of the upper boundary of the upper layer is ![]() $h(x)$ above the lowest point of the upper layer (figure 1b). The anticline extends across the region
$h(x)$ above the lowest point of the upper layer (figure 1b). The anticline extends across the region ![]() $-L < x < L$, so that
$-L < x < L$, so that ![]() $h(L)=0$. The elevation of the highest point of the anticline above the top of the parent aquifer defines the depth of the pool of
$h(L)=0$. The elevation of the highest point of the anticline above the top of the parent aquifer defines the depth of the pool of ![]() ${\rm CO}_2$ above which
${\rm CO}_2$ above which ![]() ${\rm CO}_2$ will begin to spill into the aquifer,
${\rm CO}_2$ will begin to spill into the aquifer,
We assume the layers are laterally extensive compared with the depth, ![]() $H\ll L$, so that they are approximately parallel and the height of the upper boundary of the lower layer is also
$H\ll L$, so that they are approximately parallel and the height of the upper boundary of the lower layer is also ![]() $h(x)$ relative to the height of this layer in the aquifer.
$h(x)$ relative to the height of this layer in the aquifer.
In calculating the volume of ![]() ${\rm CO}_2$ that has accumulated in a pool at the top of a layer, it is important to distinguish between the case in which
${\rm CO}_2$ that has accumulated in a pool at the top of a layer, it is important to distinguish between the case in which ![]() $H>H_{spill}$, in which case the lower surface of the pool of
$H>H_{spill}$, in which case the lower surface of the pool of ![]() ${\rm CO}_2$ is horizontal (figure 2d), and the case in which
${\rm CO}_2$ is horizontal (figure 2d), and the case in which ![]() $H< H_{spill}$. In this latter case, if the depth of the lower most boundary of the
$H< H_{spill}$. In this latter case, if the depth of the lower most boundary of the ![]() ${\rm CO}_2$ pool below the crest of the anticline,
${\rm CO}_2$ pool below the crest of the anticline, ![]() $H_p$ say, exceeds
$H_p$ say, exceeds ![]() $H$, then the lower surface of the
$H$, then the lower surface of the ![]() ${\rm CO}_2$ pool touches the lower boundary of the layer in the region
${\rm CO}_2$ pool touches the lower boundary of the layer in the region ![]() $- L^* < x < L^*$ where
$- L^* < x < L^*$ where
and in this region, the local depth of the ![]() ${\rm CO}_2$ pool,
${\rm CO}_2$ pool, ![]() $\delta (x)$ say, is
$\delta (x)$ say, is ![]() $H$. However, beyond this region, the lower boundary of the
$H$. However, beyond this region, the lower boundary of the ![]() ${\rm CO}_2$ pool is horizontal and the local thickness of the
${\rm CO}_2$ pool is horizontal and the local thickness of the ![]() ${\rm CO}_2$ pool is
${\rm CO}_2$ pool is
At the furthest extent of the pool of ![]() ${\rm CO}_2$ from the crest of the anticline,
${\rm CO}_2$ from the crest of the anticline, ![]() $L_p$ say, the depth of the pool falls to zero and so
$L_p$ say, the depth of the pool falls to zero and so ![]() $H_p = h(0)-h(L_p)$ . In each of the cases
$H_p = h(0)-h(L_p)$ . In each of the cases ![]() $H_{spill}>H$ or
$H_{spill}>H$ or ![]() $H_{spill}< H$, at each point
$H_{spill}< H$, at each point ![]() $x$, the total volume of the
$x$, the total volume of the ![]() ${\rm CO}_2$ pool, per unit distance in the anticline direction is
${\rm CO}_2$ pool, per unit distance in the anticline direction is
where ![]() $\phi$ is the porosity. In the remainder of this work we let
$\phi$ is the porosity. In the remainder of this work we let
and this leads to the expressions for the maximum volume of ![]() ${\rm CO}_2$ that can be stored in the layer,
${\rm CO}_2$ that can be stored in the layer, ![]() $V_m$, before
$V_m$, before ![]() ${\rm CO}_2$ starts to spill into the aquifer as given by
${\rm CO}_2$ starts to spill into the aquifer as given by
 \begin{equation} V_{m} = \left\{ \begin{array}{ll} \phi H_{spill}L, & H\geq H_{spill}, \\ \begin{aligned} & \phi L\left(\dfrac{H-H_{spill}}{\rm \pi}\arccos\left(\dfrac{H- H_{spill}} { H_{spill}}\right) \right. \\ & \quad+\left.H_{spill}\left[1 - \dfrac{1}{\rm \pi}\sqrt{1 - \left(\dfrac{H- H_{spill}}{H_{spill}}\right)^2}\right]\right), \end{aligned} & H< H_{spill}. \end{array} \right.\end{equation}
\begin{equation} V_{m} = \left\{ \begin{array}{ll} \phi H_{spill}L, & H\geq H_{spill}, \\ \begin{aligned} & \phi L\left(\dfrac{H-H_{spill}}{\rm \pi}\arccos\left(\dfrac{H- H_{spill}} { H_{spill}}\right) \right. \\ & \quad+\left.H_{spill}\left[1 - \dfrac{1}{\rm \pi}\sqrt{1 - \left(\dfrac{H- H_{spill}}{H_{spill}}\right)^2}\right]\right), \end{aligned} & H< H_{spill}. \end{array} \right.\end{equation}
Figure 2. Panels (a–c) illustrate three examples of layers that are filled to the spill depth with ![]() ${\rm CO}_2$ (green cap). The thickness of each layer is (a)
${\rm CO}_2$ (green cap). The thickness of each layer is (a) ![]() $H= 0.5H_{spill}$, (b)
$H= 0.5H_{spill}$, (b) ![]() $H=H_{spill}$ and (c)
$H=H_{spill}$ and (c) ![]() $H=1.25H_{spill}$. The volume of
$H=1.25H_{spill}$. The volume of ![]() ${\rm CO}_2$ in panel (b) is greater than the layer in panel (a) as the greater layer thickness allows for a greater storage volume when the
${\rm CO}_2$ in panel (b) is greater than the layer in panel (a) as the greater layer thickness allows for a greater storage volume when the ![]() ${\rm CO}_2$ pool has the spill depth. The
${\rm CO}_2$ pool has the spill depth. The ![]() ${\rm CO}_2$ volume is the same in panels (b) and (c). (d) Maximum storage volume of
${\rm CO}_2$ volume is the same in panels (b) and (c). (d) Maximum storage volume of ![]() ${\rm CO}_2$ in a single layer as a function of the layer thickness scaled with constant spill depth. We see an increase in the maximum storage volume between
${\rm CO}_2$ in a single layer as a function of the layer thickness scaled with constant spill depth. We see an increase in the maximum storage volume between ![]() $0< H\leq H_{spill}$ and then a constant maximum storage volume for
$0< H\leq H_{spill}$ and then a constant maximum storage volume for ![]() $H>H_{spill}$.
$H>H_{spill}$.
Figure 2 illustrates how the capacity of a reservoir layer increases with the layer thickness ![]() $H$ for a given value of
$H$ for a given value of ![]() $H_{spill}$, with the capacity scaled relative to the capacity of a reference aquifer in which
$H_{spill}$, with the capacity scaled relative to the capacity of a reference aquifer in which ![]() $H> H_{spill}$ ((2.6)). We can see that as
$H> H_{spill}$ ((2.6)). We can see that as ![]() $H$ increases relative to
$H$ increases relative to ![]() $H_{spill}$, the volume which can be stored in the layer increases towards the value corresponding to the case
$H_{spill}$, the volume which can be stored in the layer increases towards the value corresponding to the case ![]() $H\geq H_{spill}$, for which the lower boundary of the pool of
$H\geq H_{spill}$, for which the lower boundary of the pool of ![]() ${\rm CO}_2$ does not touch the lower boundary of the aquifer.
${\rm CO}_2$ does not touch the lower boundary of the aquifer.
2.2. Impact of capillary entry pressure on the capacity of  ${\rm CO}_2$ storage
${\rm CO}_2$ storage
The above models for the maximum volume of ![]() ${\rm CO}_2$ that can be stored are based on the geometry of the system, and the requirement that the
${\rm CO}_2$ that can be stored are based on the geometry of the system, and the requirement that the ![]() ${\rm CO}_2$ does not spill into the neighbouring aquifer. However, the layers below the top layer can only retain
${\rm CO}_2$ does not spill into the neighbouring aquifer. However, the layers below the top layer can only retain ![]() ${\rm CO}_2$ as a result of the capillary entry pressure of the overlying mudstone. In equilibrium this might reduce the storage capacity compared with the geometric estimates for the lower layers as given above. We refer to the volume associated with the capillary pressure as the static capacity.
${\rm CO}_2$ as a result of the capillary entry pressure of the overlying mudstone. In equilibrium this might reduce the storage capacity compared with the geometric estimates for the lower layers as given above. We refer to the volume associated with the capillary pressure as the static capacity.
Since the ![]() ${\rm CO}_2$ is buoyant relative to the surrounding formation fluid, the
${\rm CO}_2$ is buoyant relative to the surrounding formation fluid, the ![]() ${\rm CO}_2$ will rise initially through the permeable layer in which it is injected and accumulate below the mudstone. Owing to the density difference between the
${\rm CO}_2$ will rise initially through the permeable layer in which it is injected and accumulate below the mudstone. Owing to the density difference between the ![]() ${\rm CO}_2$ and the formation fluid,
${\rm CO}_2$ and the formation fluid, ![]() $\Delta \rho$, a buoyancy driven pressure difference across the mudstone develops, as given by
$\Delta \rho$, a buoyancy driven pressure difference across the mudstone develops, as given by
Here ![]() $\delta (x)$ is the depth of the
$\delta (x)$ is the depth of the ![]() ${\rm CO}_2$ pool. In equilibrium this buoyancy pressure will match the mudstone capillary entry pressure
${\rm CO}_2$ pool. In equilibrium this buoyancy pressure will match the mudstone capillary entry pressure ![]() $P_c$ so that
$P_c$ so that
If the geometry of the system is such that the thickness of the layers is greater than the spill height (![]() $H>H_{spill}$), then the maximum volume of
$H>H_{spill}$), then the maximum volume of ![]() ${\rm CO}_2$ in the lower layer arises when the pool has depth
${\rm CO}_2$ in the lower layer arises when the pool has depth ![]() $\delta ^*$.
$\delta ^*$.
However, if the thickness of the layers is less than the spill height, then the pool of ![]() ${\rm CO}_2$ in the upper layer may contact the lower mudstone layer. For static equilibrium, the pool of
${\rm CO}_2$ in the upper layer may contact the lower mudstone layer. For static equilibrium, the pool of ![]() ${\rm CO}_2$ in the layer below can only extend a distance
${\rm CO}_2$ in the layer below can only extend a distance ![]() $\delta ^*$ below the base of the pool of
$\delta ^*$ below the base of the pool of ![]() ${\rm CO}_2$ in the upper layer. The maximum depth in the lower layer for equilibrium is therefore
${\rm CO}_2$ in the upper layer. The maximum depth in the lower layer for equilibrium is therefore ![]() $\delta ^* - (H_{spill} - H)$. This effect needs to be included when calculating the static capacity.
$\delta ^* - (H_{spill} - H)$. This effect needs to be included when calculating the static capacity.
To proceed we explore how the static capacity evolves with capillary entry pressure for a given geometry. For convenience, we scale the capillary entry pressure of the mudstone relative to the hydrostatic pressure at the point of spilling to get
We first choose a geometry where ![]() $H/H_{spill} = 1.25$ so that there is no overlapping of the pools. In this case the pool of
$H/H_{spill} = 1.25$ so that there is no overlapping of the pools. In this case the pool of ![]() ${\rm CO}_2$ in the upper layer does not touch the lower mudstone layer. In panel I of figure 3 we see an illustration of the static capacity when
${\rm CO}_2$ in the upper layer does not touch the lower mudstone layer. In panel I of figure 3 we see an illustration of the static capacity when ![]() $H/H_{spill} = 1.25$ and
$H/H_{spill} = 1.25$ and ![]() $P^* = 0$. In this case there is no capillary entry pressure in the mudstone layer so that in equilibrium no
$P^* = 0$. In this case there is no capillary entry pressure in the mudstone layer so that in equilibrium no ![]() ${\rm CO}_2$ is retained in the lower layer. In panel II,
${\rm CO}_2$ is retained in the lower layer. In panel II, ![]() $P^* = 0.25$ and we see that some
$P^* = 0.25$ and we see that some ![]() ${\rm CO}_2$ is retained in the lower layer with the depth of the
${\rm CO}_2$ is retained in the lower layer with the depth of the ![]() ${\rm CO}_2$ in the lower layer being
${\rm CO}_2$ in the lower layer being ![]() $\delta ^* = 0.25$. In panel III,
$\delta ^* = 0.25$. In panel III, ![]() $P^*=1$ so that the lower layer is filled to the spill depth at the static capacity. This case represents the maximum volume of
$P^*=1$ so that the lower layer is filled to the spill depth at the static capacity. This case represents the maximum volume of ![]() ${\rm CO}_2$ that can be stored and we scale the static capacities relative to this case. Panels IV–VI and VII–IX show cases where
${\rm CO}_2$ that can be stored and we scale the static capacities relative to this case. Panels IV–VI and VII–IX show cases where ![]() $H< H_{spill}$. In these cases the depth in the lower layer is a distance
$H< H_{spill}$. In these cases the depth in the lower layer is a distance ![]() $\delta ^*$ below the lower boundary of the
$\delta ^*$ below the lower boundary of the ![]() ${\rm CO}_2$ pool in the upper layer. This means that in cases with smaller
${\rm CO}_2$ pool in the upper layer. This means that in cases with smaller ![]() $H$, the lower layer will reach the spill depth at smaller values of
$H$, the lower layer will reach the spill depth at smaller values of ![]() $P^*$. This is illustrated in panel X in which we illustrate the static capacity as a function of
$P^*$. This is illustrated in panel X in which we illustrate the static capacity as a function of ![]() $\delta ^*/H_{spill}$; for a given geometry, there is a maximum static capacity corresponding to the case for which
$\delta ^*/H_{spill}$; for a given geometry, there is a maximum static capacity corresponding to the case for which ![]() $\delta ^* = H/H_{spill}$.
$\delta ^* = H/H_{spill}$.

Figure 3. Panels I–IX show cartoons of a series of two layered anticline systems where the upper layer is filled to the spill depth and the lower layer is filled to the dimensionless capillary entry pressure depth, ![]() $\delta ^*$, so that there is no migration of fluid across the mudstone and the system is in static equilibrium. Panels I–III correspond to the case where
$\delta ^*$, so that there is no migration of fluid across the mudstone and the system is in static equilibrium. Panels I–III correspond to the case where ![]() $H/H_{spill} = 1.25$ and
$H/H_{spill} = 1.25$ and ![]() $\delta ^*/H_{spill} = 0$ (panel I),
$\delta ^*/H_{spill} = 0$ (panel I), ![]() $0.25$ (panel II) and
$0.25$ (panel II) and ![]() $1.0$ (panel III). In panels IV–VI,
$1.0$ (panel III). In panels IV–VI, ![]() $H/H_{spill} = 0.75$ and
$H/H_{spill} = 0.75$ and ![]() $\delta ^*/H_{spill} = 0$ (panel IV),
$\delta ^*/H_{spill} = 0$ (panel IV), ![]() $0.25$ (panel V) and
$0.25$ (panel V) and ![]() $0.75$ (panel VI). In panels VII–IX,
$0.75$ (panel VI). In panels VII–IX, ![]() $H /H_{spill} = 0.25$ and
$H /H_{spill} = 0.25$ and ![]() $\delta ^*/H_{spill} = 0$ (panel VII),
$\delta ^*/H_{spill} = 0$ (panel VII), ![]() $0.13$ (panel VIII) and
$0.13$ (panel VIII) and ![]() $0.25$ (panel IX). Panel X: Illustration of the static storage capacity as a function of the capillary entry depth scaled with the spill depth for the three geometries (
$0.25$ (panel IX). Panel X: Illustration of the static storage capacity as a function of the capillary entry depth scaled with the spill depth for the three geometries (![]() $H/H_{spill} = 1.0$, solid, 0.75, dashed and 0.25 dot-dashed). We scale the static storage capacities relative to the case for which
$H/H_{spill} = 1.0$, solid, 0.75, dashed and 0.25 dot-dashed). We scale the static storage capacities relative to the case for which ![]() $H = H_{spill}$ and
$H = H_{spill}$ and ![]() $\delta ^* = 1.0$.
$\delta ^* = 1.0$.
3. Dynamic filling of the system
We now consider injection of ![]() ${\rm CO}_2$ into the base of a two layered reservoir and explore how the system fills with time until one of the layers has filled to the point of spilling.
${\rm CO}_2$ into the base of a two layered reservoir and explore how the system fills with time until one of the layers has filled to the point of spilling.
3.1. Initial filling prior to filling in the upper layer
At early times ![]() ${\rm CO}_2$ will accumulate in the lower layer below the mudstone while the capillary entry pressure of the mudstone prevents
${\rm CO}_2$ will accumulate in the lower layer below the mudstone while the capillary entry pressure of the mudstone prevents ![]() ${\rm CO}_2$ entering the upper layer (figure 4a).
${\rm CO}_2$ entering the upper layer (figure 4a).

Figure 4. Schematic diagrams of injection into the lower layer of a two layered system at three times during injection. Here the layer thickness is less than the spill depth so that the pool of ![]() ${\rm CO}_2$ in the upper layer may touch the mudstone below. (a) The green arrow shows a flux of
${\rm CO}_2$ in the upper layer may touch the mudstone below. (a) The green arrow shows a flux of ![]() ${\rm CO}_2$ into layer
${\rm CO}_2$ into layer ![]() $1$ and the green pool is the accumulation of
$1$ and the green pool is the accumulation of ![]() ${\rm CO}_2$ forming below the mudstone. At early times the pool of
${\rm CO}_2$ forming below the mudstone. At early times the pool of ![]() ${\rm CO}_2$ in the injection layer deepens and there is no flow across the mudstone until the depth of the pool reaches the capillary entry height
${\rm CO}_2$ in the injection layer deepens and there is no flow across the mudstone until the depth of the pool reaches the capillary entry height ![]() $\delta ^*$. (b) At a later time when the depth of the
$\delta ^*$. (b) At a later time when the depth of the ![]() ${\rm CO}_2$ pool is sufficient such that the hydrostatic pressure exceeds the mudstone capillary entry pressure and a pool of
${\rm CO}_2$ pool is sufficient such that the hydrostatic pressure exceeds the mudstone capillary entry pressure and a pool of ![]() ${\rm CO}_2$ begins to form in the upper layer. (c) At a later time the pool of
${\rm CO}_2$ begins to form in the upper layer. (c) At a later time the pool of ![]() ${\rm CO}_2$ in the upper layer reaches the mudstone below leading to a further deepening of the pool in the lower layer. In this panel we see the depth of
${\rm CO}_2$ in the upper layer reaches the mudstone below leading to a further deepening of the pool in the lower layer. In this panel we see the depth of ![]() ${\rm CO}_2$ in layer
${\rm CO}_2$ in layer ![]() $2$ has passed the spill point where
$2$ has passed the spill point where ![]() ${\rm CO}_2$ begins to spill into the neighbouring aquifer.
${\rm CO}_2$ begins to spill into the neighbouring aquifer.
The ![]() ${\rm CO}_2$ pool in the lower layer deepens as
${\rm CO}_2$ pool in the lower layer deepens as
where ![]() $Q_{in}$ is the source flux, neglecting the volume occupied by the plume of
$Q_{in}$ is the source flux, neglecting the volume occupied by the plume of ![]() ${\rm CO}_2$ between the injection well and the
${\rm CO}_2$ between the injection well and the ![]() ${\rm CO}_2$ pool, which will be small in a relatively wide and shallow anticline system.
${\rm CO}_2$ pool, which will be small in a relatively wide and shallow anticline system.
3.2. Filling with drainage into the upper mudstone layer
Once the buoyancy head of the ![]() ${\rm CO}_2$ in the lower layer exceeds the capillary entry pressure of the mudstone,
${\rm CO}_2$ in the lower layer exceeds the capillary entry pressure of the mudstone, ![]() ${\rm CO}_2$ can flow into the upper layer, forming a second pool of
${\rm CO}_2$ can flow into the upper layer, forming a second pool of ![]() ${\rm CO}_2$. If
${\rm CO}_2$. If ![]() $H< H_{spill}$, the pool of
$H< H_{spill}$, the pool of ![]() ${\rm CO}_2$ in the upper layer may eventually contact the upper surface of the mudstone. In this case, the continuing drainage of
${\rm CO}_2$ in the upper layer may eventually contact the upper surface of the mudstone. In this case, the continuing drainage of ![]() ${\rm CO}_2$ through the mudstone and deepening of the upper pool of
${\rm CO}_2$ through the mudstone and deepening of the upper pool of ![]() ${\rm CO}_2$ will also require a gradual deepening of the pool of
${\rm CO}_2$ will also require a gradual deepening of the pool of ![]() ${\rm CO}_2$ in the lower layer so that the buoyancy head of the
${\rm CO}_2$ in the lower layer so that the buoyancy head of the ![]() ${\rm CO}_2$ in the lower layer remains in excess of the capillary entry pressure (figure 4b). In figure 4(b) the flow from the lower to the upper layer has Darcy speed
${\rm CO}_2$ in the lower layer remains in excess of the capillary entry pressure (figure 4b). In figure 4(b) the flow from the lower to the upper layer has Darcy speed
where ![]() $k_m$ and
$k_m$ and ![]() $b_m$ are the permeability and thickness of the mudstone,
$b_m$ are the permeability and thickness of the mudstone, ![]() $\mu _c$ is the viscosity of the
$\mu _c$ is the viscosity of the ![]() ${\rm CO}_2$ and
${\rm CO}_2$ and ![]() $\delta _1(x)$ is the buoyancy head of
$\delta _1(x)$ is the buoyancy head of ![]() ${\rm CO}_2$ in layer 2 relative to layer 1 at point
${\rm CO}_2$ in layer 2 relative to layer 1 at point ![]() $x$. The draining zone extends a distance
$x$. The draining zone extends a distance ![]() $L_1$ from the crest of the anticline where
$L_1$ from the crest of the anticline where
and the total flux of ![]() ${\rm CO}_2$ from layer
${\rm CO}_2$ from layer ![]() $1$ to
$1$ to ![]() $2$ is
$2$ is
In cases where the spill depth is greater than the thickness of the storage layers, the pools of ![]() ${\rm CO}_2$ may both be in contact with the mudstone. Figure 4(c) shows an example of the upper pool of
${\rm CO}_2$ may both be in contact with the mudstone. Figure 4(c) shows an example of the upper pool of ![]() ${\rm CO}_2$ touching the mudstone in the region,
${\rm CO}_2$ touching the mudstone in the region, ![]() $-L^*_1< x< L^*_1$, the hydrostatic pressure difference across the mudstone is constant and given by
$-L^*_1< x< L^*_1$, the hydrostatic pressure difference across the mudstone is constant and given by ![]() $\rho g \Delta h_{1,2}$, where
$\rho g \Delta h_{1,2}$, where ![]() $\Delta h_{1,2}$ is the vertical distance between the lower boundary of the two pools of
$\Delta h_{1,2}$ is the vertical distance between the lower boundary of the two pools of ![]() ${\rm CO}_2$. The Darcy speed in this region is
${\rm CO}_2$. The Darcy speed in this region is
In the region ![]() $L_1> x>L^*_1$, the buoyancy force gradually decreases, until reaching the critical point where it matches the capillary entry pressure,
$L_1> x>L^*_1$, the buoyancy force gradually decreases, until reaching the critical point where it matches the capillary entry pressure, ![]() $x=L_1$. The total flux from layer 1 to layer 2 is then
$x=L_1$. The total flux from layer 1 to layer 2 is then
 \begin{equation} Q_{1,2} = \left\{ \begin{array}{@{}ll} \displaystyle \dfrac{2k\phi d}{\mu b}\int_{0}^{L_{1}}u_{1,2}(x){{\rm d} x}, & \delta_2 (0) < H, \\ \displaystyle \dfrac{2k\phi d}{\mu b}\left(\int_{L^*_1}^{L_{1}}u_{1,2}(x) {{\rm d} x} + \int_{0}^{L^*_1}u^*_{1,2}(x){{\rm d} x} \right), & \delta_2 (0) > H. \end{array} \right. \end{equation}
\begin{equation} Q_{1,2} = \left\{ \begin{array}{@{}ll} \displaystyle \dfrac{2k\phi d}{\mu b}\int_{0}^{L_{1}}u_{1,2}(x){{\rm d} x}, & \delta_2 (0) < H, \\ \displaystyle \dfrac{2k\phi d}{\mu b}\left(\int_{L^*_1}^{L_{1}}u_{1,2}(x) {{\rm d} x} + \int_{0}^{L^*_1}u^*_{1,2}(x){{\rm d} x} \right), & \delta_2 (0) > H. \end{array} \right. \end{equation}The volume in layer 1 thus evolves according to the relation
where ![]() $Q_{in}$ is the supply flux. In the upper layer, the volume evolves according to the relation
$Q_{in}$ is the supply flux. In the upper layer, the volume evolves according to the relation
In figure 4(c) we also see that the upper layer has exceeded the spill point and ![]() ${\rm CO}_2$ spills into the neighbouring aquifer. Throughout this analysis we assume that such unconfined spreading of the
${\rm CO}_2$ spills into the neighbouring aquifer. Throughout this analysis we assume that such unconfined spreading of the ![]() ${\rm CO}_2$ would not be acceptable, and so injection should be stopped prior to reaching this point.
${\rm CO}_2$ would not be acceptable, and so injection should be stopped prior to reaching this point.
3.3. Dimensionless parameters
To simplify the analysis, we introduce a series of scalings for the injection rate to complement the dimensionless capillary entry pressure (2.9). The maximum flux through the mudstone per unit distance into the anticline is
This flux arises when the lower layer is filled to the spill point and the capillary entry pressure is zero. The dimensionless supply flux is given by
The dimensionless depth and length, denoted by the hat notation are given by ![]() $h(x) = \hat {h}H_{spill}$,
$h(x) = \hat {h}H_{spill}$, ![]() $x = \hat {x}L$ and we scale time according to the time to fill one of the layers,
$x = \hat {x}L$ and we scale time according to the time to fill one of the layers,
The case ![]() $P^*=1$ corresponds to the maximum capillary pressure for which there is any flow into the upper layer prior to
$P^*=1$ corresponds to the maximum capillary pressure for which there is any flow into the upper layer prior to ![]() ${\rm CO}_2$ spilling into the aquifer from the lower layer. The ratio of the spill depth and the layer depth,
${\rm CO}_2$ spilling into the aquifer from the lower layer. The ratio of the spill depth and the layer depth, ![]() $\alpha = H/H_{spill}$, determines whether during filling of the upper layer the
$\alpha = H/H_{spill}$, determines whether during filling of the upper layer the ![]() ${\rm CO}_2$ pool in the upper layer can touch the upper surface of the mudstone,
${\rm CO}_2$ pool in the upper layer can touch the upper surface of the mudstone, ![]() $\alpha <1$, or whether the pool remains well above the mudstone horizon,
$\alpha <1$, or whether the pool remains well above the mudstone horizon, ![]() $\alpha >1$.
$\alpha >1$.
We now drop the hat notation and work with dimensionless quantities.
4. Model predictions
The volume of ![]() ${\rm CO}_2$ that can be injected before
${\rm CO}_2$ that can be injected before ![]() ${\rm CO}_2$ spills into the aquifer from either the upper or lower layer depends on the injection rate and the capillary entry pressure. We examine injection in a two layered system for a range of cases considering both (i)
${\rm CO}_2$ spills into the aquifer from either the upper or lower layer depends on the injection rate and the capillary entry pressure. We examine injection in a two layered system for a range of cases considering both (i) ![]() $\alpha >1$ and (ii)
$\alpha >1$ and (ii) ![]() $\alpha <1$. We solve ((3.7) and (3.8)) numerically with initial conditions
$\alpha <1$. We solve ((3.7) and (3.8)) numerically with initial conditions ![]() $\delta _1(x) = 0$ and
$\delta _1(x) = 0$ and ![]() $\delta _2(x) = 0$ at
$\delta _2(x) = 0$ at ![]() $t=0$. In general, with a high injection rate, we find that the pool in the lower layer first reaches the spill point, while for low injection rates, the upper layer first reaches the spill point. In the transitional case, both layers spill at the same time, and this enables the maximum injection of
$t=0$. In general, with a high injection rate, we find that the pool in the lower layer first reaches the spill point, while for low injection rates, the upper layer first reaches the spill point. In the transitional case, both layers spill at the same time, and this enables the maximum injection of ![]() ${\rm CO}_2$ prior to any spilling. However, we also show that post-injection there may be some migration of
${\rm CO}_2$ prior to any spilling. However, we also show that post-injection there may be some migration of ![]() ${\rm CO}_2$ from the lower to the upper layer and for a range of cases near the transitional case, this can lead to some spilling from the upper layer.
${\rm CO}_2$ from the lower to the upper layer and for a range of cases near the transitional case, this can lead to some spilling from the upper layer.
4.1. Layer thickness greater than spill height ( $\alpha \geq 1$)
$\alpha \geq 1$)
In figure 5(a–d), we present simulations for ![]() $\alpha = 1.25$ illustrating the depth of the
$\alpha = 1.25$ illustrating the depth of the ![]() ${\rm CO}_2$ pools in the upper (red) and lower (blue) layers as a function of time, for cases I.A–IV.A (marked on figure 6a). In figure 5(a) we present the case
${\rm CO}_2$ pools in the upper (red) and lower (blue) layers as a function of time, for cases I.A–IV.A (marked on figure 6a). In figure 5(a) we present the case ![]() $Q_{in} = 0.25$ and
$Q_{in} = 0.25$ and ![]() $P^*=0.15$ (case I.A, figure 6a). We find that the depth of the pool in the lower layer approaches a dynamic equilibrium height as the depth in the upper layer reaches the spill height.
$P^*=0.15$ (case I.A, figure 6a). We find that the depth of the pool in the lower layer approaches a dynamic equilibrium height as the depth in the upper layer reaches the spill height.

Figure 6. Variation of the critical capillary pressure (![]() $x$ axis) as a function of the injection rate
$x$ axis) as a function of the injection rate ![]() $P^*_c (Q_{in})$,
$P^*_c (Q_{in})$, ![]() $f$ (
$f$ (![]() $y$ axis). For
$y$ axis). For ![]() $P^*>P^*_c$, the lower layer spills first. Panel (a) corresponds to
$P^*>P^*_c$, the lower layer spills first. Panel (a) corresponds to ![]() $\alpha = 1.25$ and panel (b) corresponds to the
$\alpha = 1.25$ and panel (b) corresponds to the ![]() $\alpha = 0.5$ case. The specific calculations are shown in figure 5, with parameter values indicated in the figure.
$\alpha = 0.5$ case. The specific calculations are shown in figure 5, with parameter values indicated in the figure.
In figure 5(b) we look at a larger injection rate of ![]() $Q_{in} = 1.05$ (case II.A, figure 6a). In this case the depth of
$Q_{in} = 1.05$ (case II.A, figure 6a). In this case the depth of ![]() ${\rm CO}_2$ in each layer reaches the spill point at the same time. If the lower layer reaches the spill point, then the dynamic equilibrium depth in the lower layer is greater than the spill depth. It follows that with even larger injection rates the lower layer reaches the spill depth more rapidly and before the pool in the upper layer (e.g. Figure 5(c), case III.A, figure 6a).
${\rm CO}_2$ in each layer reaches the spill point at the same time. If the lower layer reaches the spill point, then the dynamic equilibrium depth in the lower layer is greater than the spill depth. It follows that with even larger injection rates the lower layer reaches the spill depth more rapidly and before the pool in the upper layer (e.g. Figure 5(c), case III.A, figure 6a).
From (3.7) we expect that increasing the capillary pressure, ![]() $P^*$, will increase the dynamic equilibrium depth in the injection layer. In figure 5(d) we present a calculation with
$P^*$, will increase the dynamic equilibrium depth in the injection layer. In figure 5(d) we present a calculation with ![]() $P^* = 0.6$ (IV.A, figure 6a); this has the same injection rate as in panel (b). As expected, this results in a continued and more rapid filling of the lower layer and the
$P^* = 0.6$ (IV.A, figure 6a); this has the same injection rate as in panel (b). As expected, this results in a continued and more rapid filling of the lower layer and the ![]() ${\rm CO}_2$ pool in the lower layer reaches the spill point first.
${\rm CO}_2$ pool in the lower layer reaches the spill point first.
It follows by continuity that there is a range of values of ![]() $Q_{in}$ for which there is a critical capillary pressure
$Q_{in}$ for which there is a critical capillary pressure ![]() $P^* = P^*_c(Q_{in})$, for which both layers reach the spill point at the same time and if
$P^* = P^*_c(Q_{in})$, for which both layers reach the spill point at the same time and if ![]() $P^*>P^*_c(Q_{in})$ then the system is predicted to spill from the lower layer first. We show the curve
$P^*>P^*_c(Q_{in})$ then the system is predicted to spill from the lower layer first. We show the curve ![]() $P^*_c(Q_{in})$ in figure 6(a).
$P^*_c(Q_{in})$ in figure 6(a).
4.2. Layer thickness less than spill height ( $\alpha < 1$)
$\alpha < 1$)
In figure 5(e–h) we present a complimentary series of simulations for the case ![]() $\alpha = 0.5$ (figure 6(b), cases I.B–IV.B). Figure 5(e) shows the case
$\alpha = 0.5$ (figure 6(b), cases I.B–IV.B). Figure 5(e) shows the case ![]() $Q_{in} = 0.2$ and
$Q_{in} = 0.2$ and ![]() $P^* = 0.2$ (case I.B, figure 6b). The depth in the lower layer increases initially until reaching the minimum height for drainage into the upper layer and then
$P^* = 0.2$ (case I.B, figure 6b). The depth in the lower layer increases initially until reaching the minimum height for drainage into the upper layer and then ![]() ${\rm CO}_2$ begins to drain into the upper layer. The lower layer then approaches the equilibrium depth while the upper layer continues to deepen and eventually fills to contact the mudstone layer at around
${\rm CO}_2$ begins to drain into the upper layer. The lower layer then approaches the equilibrium depth while the upper layer continues to deepen and eventually fills to contact the mudstone layer at around ![]() $t=3.3$. In order for the flux to continue through the mudstone, the lower layer of
$t=3.3$. In order for the flux to continue through the mudstone, the lower layer of ![]() ${\rm CO}_2$ begins to deepen again and eventually the upper layer reaches the spill point. If the injection rate is greater, as in the case
${\rm CO}_2$ begins to deepen again and eventually the upper layer reaches the spill point. If the injection rate is greater, as in the case ![]() $Q_{in} = 0.57$,
$Q_{in} = 0.57$, ![]() $P^* = 0.20$ (II.B, figure 6b), the initial equilibrium depth of the pool of
$P^* = 0.20$ (II.B, figure 6b), the initial equilibrium depth of the pool of ![]() ${\rm CO}_2$ in the lower layer is greater. In this case, once the upper layer fills to reach the mudstone, the pool of
${\rm CO}_2$ in the lower layer is greater. In this case, once the upper layer fills to reach the mudstone, the pool of ![]() ${\rm CO}_2$ in the lower layer continues to deepen, and both layers now reach the spill condition at the same time (figure 5f). If the injection rate is greater still so that
${\rm CO}_2$ in the lower layer continues to deepen, and both layers now reach the spill condition at the same time (figure 5f). If the injection rate is greater still so that ![]() $Q_{in} = 1.3$ (case III.B, figure 6b) the pool of
$Q_{in} = 1.3$ (case III.B, figure 6b) the pool of ![]() ${\rm CO}_2$ in the lower layer deepens sufficiently quickly that this layer now spills first (figure 5g).
${\rm CO}_2$ in the lower layer deepens sufficiently quickly that this layer now spills first (figure 5g).
As for the ![]() $\alpha >1$ case, with larger values of capillary pressure the dynamic equilibrium depth in the lower layer also increases. For example, if we compare cases II.B and IV.B (figure 6b), the case with the larger capillary pressure leads to spilling from the lower layer (case IV.B, figure 5h) while the case with smaller capillary pressure leads to both layers spilling at the same time (case II.B, figure 5f).
$\alpha >1$ case, with larger values of capillary pressure the dynamic equilibrium depth in the lower layer also increases. For example, if we compare cases II.B and IV.B (figure 6b), the case with the larger capillary pressure leads to spilling from the lower layer (case IV.B, figure 5h) while the case with smaller capillary pressure leads to both layers spilling at the same time (case II.B, figure 5f).
Again, we have built a regime diagram to delineate whether spilling first occurs from the upper or lower layer during injection as a function of the injection rate and the capillary pressure (figure 6b). For injection rates larger than the critical value, the lower layer spills first, in an analogous fashion to the ![]() $\alpha = 1.25$ case.
$\alpha = 1.25$ case.
4.3. Post-injection drainage
In the above model calculations, we stop the calculation once the depth of the ![]() ${\rm CO}_2$ reaches the depth at which it spills in one of the layers. However, the
${\rm CO}_2$ reaches the depth at which it spills in one of the layers. However, the ![]() ${\rm CO}_2$ pool in the lower layer can continue to drain into the upper layer even once the injection has stopped. If there is sufficient
${\rm CO}_2$ pool in the lower layer can continue to drain into the upper layer even once the injection has stopped. If there is sufficient ![]() ${\rm CO}_2$ that can drain from the lower layer to the upper layer, then some
${\rm CO}_2$ that can drain from the lower layer to the upper layer, then some ![]() ${\rm CO}_2$ may ultimately spill from the upper layer a certain time after the injection. To model the post-injection drainage, we solve (3.7) and (3.8) setting
${\rm CO}_2$ may ultimately spill from the upper layer a certain time after the injection. To model the post-injection drainage, we solve (3.7) and (3.8) setting ![]() $Q_{in}=0$, and using the depths at the moment injection was stopped as the initial condition. In figure 7(a) we present a case in which both the
$Q_{in}=0$, and using the depths at the moment injection was stopped as the initial condition. In figure 7(a) we present a case in which both the ![]() ${\rm CO}_2$ pools reach the spill depth at approximately the same time during injection (case II.B, figure 6b). After injection has stopped
${\rm CO}_2$ pools reach the spill depth at approximately the same time during injection (case II.B, figure 6b). After injection has stopped ![]() ${\rm CO}_2$ continues to drain into the upper layer, which is already at the spill depth, so that spilling occurs in the upper layer.
${\rm CO}_2$ continues to drain into the upper layer, which is already at the spill depth, so that spilling occurs in the upper layer.

Figure 7. Variation of the ![]() ${\rm CO}_2$ pool depth as a function of time during injection and once injection has stopped. In all three panels
${\rm CO}_2$ pool depth as a function of time during injection and once injection has stopped. In all three panels ![]() $P^* = 0.2$. In each panel the red dashed line shows the spill depth, the black dashed line shows the time at which injection is stopped and the solid blue and red lines denote the depth of
$P^* = 0.2$. In each panel the red dashed line shows the spill depth, the black dashed line shows the time at which injection is stopped and the solid blue and red lines denote the depth of ![]() ${\rm CO}_2$ in the lower and upper layers, respectively. For each simulation,
${\rm CO}_2$ in the lower and upper layers, respectively. For each simulation, ![]() ${\rm CO}_2$ is injected until one of the layers is full and then injection is stopped. (a) During injection
${\rm CO}_2$ is injected until one of the layers is full and then injection is stopped. (a) During injection ![]() $Q_{in} = 0.57$. Here both layers reach the spill point when injection stops. Once injection is stopped,
$Q_{in} = 0.57$. Here both layers reach the spill point when injection stops. Once injection is stopped, ![]() ${\rm CO}_2$ continues to drain into the upper layer. As the depth in the upper layer was already at the spill point, this leads to spilling of
${\rm CO}_2$ continues to drain into the upper layer. As the depth in the upper layer was already at the spill point, this leads to spilling of ![]() ${\rm CO}_2$ from the upper layer. (b) During injection
${\rm CO}_2$ from the upper layer. (b) During injection ![]() $Q_{in}= 0.8$. Here the lower layer reaches the spill point during injection and there is some remaining capacity for
$Q_{in}= 0.8$. Here the lower layer reaches the spill point during injection and there is some remaining capacity for ![]() ${\rm CO}_2$ in the upper layer. After injection the layers reach equilibrium just before the depth in the upper layer reaches the spill depth. (c) During injection
${\rm CO}_2$ in the upper layer. After injection the layers reach equilibrium just before the depth in the upper layer reaches the spill depth. (c) During injection ![]() $Q_{in} = 1.3$. The system reaches equilibrium well before the
$Q_{in} = 1.3$. The system reaches equilibrium well before the ![]() ${\rm CO}_2$ in the upper layer reaches the spill depth.
${\rm CO}_2$ in the upper layer reaches the spill depth.
In figure 7(b) we consider an additional case at a greater injection flux of ![]() $Q_{in} = 0.8$, so that the lower layer reaches the spill point during injection. After injection the depth in the lower layer decreases towards the capillary entry depth as
$Q_{in} = 0.8$, so that the lower layer reaches the spill point during injection. After injection the depth in the lower layer decreases towards the capillary entry depth as ![]() ${\rm CO}_2$ continues to drain into the upper layer. In this case, once the depth in the lower layer reaches this minimum depth for flow, the upper layer is precisely at the spill depth. If we consider a case where either the injection rate or capillary entry pressure is greater, then less
${\rm CO}_2$ continues to drain into the upper layer. In this case, once the depth in the lower layer reaches this minimum depth for flow, the upper layer is precisely at the spill depth. If we consider a case where either the injection rate or capillary entry pressure is greater, then less ![]() ${\rm CO}_2$ will drain into the upper layer during injection. This means that once injection has stopped, the system will reach equilibrium without spilling from the upper layer. Figure 7(c) shows a case with a greater injection flux (case III.B, figure 6b) and shows that once injection is stopped, the system reaches equilibrium with spare capacity in the upper layer.
${\rm CO}_2$ will drain into the upper layer during injection. This means that once injection has stopped, the system will reach equilibrium without spilling from the upper layer. Figure 7(c) shows a case with a greater injection flux (case III.B, figure 6b) and shows that once injection is stopped, the system reaches equilibrium with spare capacity in the upper layer.
In cases where there is spare capacity in the upper layer after post-injection drainage, the total storage volume stored will be less than the static capacity of the anticline. Consequently, there is a range of capillary entry pressures (![]() $0< P^*\leq 0.5$ for
$0< P^*\leq 0.5$ for ![]() $\alpha = 0.5$) for which there is an upper bound on the injection rate,
$\alpha = 0.5$) for which there is an upper bound on the injection rate, ![]() $Q_{max}(P^*)$, in order to achieve the static capacity of the system. When injecting at rates below this upper bound, the injection should be stopped when the static capacity has been reached in order to avoid spilling after injection.
$Q_{max}(P^*)$, in order to achieve the static capacity of the system. When injecting at rates below this upper bound, the injection should be stopped when the static capacity has been reached in order to avoid spilling after injection.
In figure 8(a) we present contours of the volume of ![]() ${\rm CO}_2$ injected if injection continues until one of the layers reaches the spill point. The black dashed line corresponds to the critical capillary pressure
${\rm CO}_2$ injected if injection continues until one of the layers reaches the spill point. The black dashed line corresponds to the critical capillary pressure ![]() $P^*_c(Q_{in})$ shown in figure 6(b), for which both of the layers reach the spill point at the same time. The red dashed line shows the maximum injection rate
$P^*_c(Q_{in})$ shown in figure 6(b), for which both of the layers reach the spill point at the same time. The red dashed line shows the maximum injection rate ![]() $Q_{max}(P^*)$ as defined as the injection rate at which
$Q_{max}(P^*)$ as defined as the injection rate at which ![]() ${\rm CO}_2$ will drain into the upper layer after injection such that the upper layer becomes completely full at static equilibrium without any
${\rm CO}_2$ will drain into the upper layer after injection such that the upper layer becomes completely full at static equilibrium without any ![]() ${\rm CO}_2$ spilling from the upper layer. For each injection rate
${\rm CO}_2$ spilling from the upper layer. For each injection rate ![]() $Q< Q_{max}$, injection should be stopped when the injection volume matches the static capacity to prevent any spilling of
$Q< Q_{max}$, injection should be stopped when the injection volume matches the static capacity to prevent any spilling of ![]() ${\rm CO}_2$ into the aquifer. For injection rates
${\rm CO}_2$ into the aquifer. For injection rates ![]() $Q>Q_{max}$, injection until the lower layer reaches the spill point will result in an injection volume smaller than the static capacity. Figure 8(b) shows contours of the maximum storage volume as a function of injection rate and capillary entry pressure, when accounting for this post-injection drainage.
$Q>Q_{max}$, injection until the lower layer reaches the spill point will result in an injection volume smaller than the static capacity. Figure 8(b) shows contours of the maximum storage volume as a function of injection rate and capillary entry pressure, when accounting for this post-injection drainage.

Figure 8. (a) Contours of volume stored during injection if one the layers is filled to the spill point as a function of ![]() $P^*$ and
$P^*$ and ![]() $Q_{in}$ for the case
$Q_{in}$ for the case ![]() $\alpha = 0.5$. The black dashed line shows the boundary between spilling in the upper layer versus spilling in the lower layer. The red dashed line shows the critical injection rate as a function of capillary pressure such that with smaller injection rates, it is possible to inject more
$\alpha = 0.5$. The black dashed line shows the boundary between spilling in the upper layer versus spilling in the lower layer. The red dashed line shows the critical injection rate as a function of capillary pressure such that with smaller injection rates, it is possible to inject more ![]() ${\rm CO}_2$ than the static capacity of the reservoir before any
${\rm CO}_2$ than the static capacity of the reservoir before any ![]() ${\rm CO}_2$ spills from either layer of the system. In this case, the post injection drainage to the upper layer can then lead to
${\rm CO}_2$ spills from either layer of the system. In this case, the post injection drainage to the upper layer can then lead to ![]() ${\rm CO}_2$ spilling from the upper layer, unless the injection is stopped when a volume equal to the static capacity has been injected. (b) Contours of the maximum storage volume of
${\rm CO}_2$ spilling from the upper layer, unless the injection is stopped when a volume equal to the static capacity has been injected. (b) Contours of the maximum storage volume of ![]() ${\rm CO}_2$ as a function of
${\rm CO}_2$ as a function of ![]() $P^*$ and
$P^*$ and ![]() $Q_{in}$ when accounting for the post-injection redistribution of
$Q_{in}$ when accounting for the post-injection redistribution of ![]() ${\rm CO}_2$, in order to prevent any spillage from the system. Contours of (a) injection volume and (b) storage volume.
${\rm CO}_2$, in order to prevent any spillage from the system. Contours of (a) injection volume and (b) storage volume.
Comparison with figure 8(a) illustrates the reduction in the total injected volume to prevent post injection spillage. Note that for all injection rates below the critical injection rate (red dashed line), the system can be filled to the maximum storage capacity provided the injection is stopped once the volume in the lower and upper layer match this maximum value. Note that in the figures, the volume in the system is normalised relative to the case in which both layers are filled to the spill point.
5. Analogue experiments
In order to test elements of the model described above, we carried out some simple experiments in which air is injected to displace water in a layered bead pack. Figure 9(a) displays a schematic of our experimental system in which we have a tank of dimensions ![]() $120 \times 10 \times 290$ mm in which two different sizes of spherical beads (of a diameter 1 and 3 mm) are arranged to create a system of two permeable layers of 3 mm beads, separated by a much less permeable layer, composed of 1 mm beads. This represents an idealised cross-section through an anticline-type feature. Above the upper layer of beads, there is a layer of impermeable putty to prevent air migrating further up the system. There is a pressure relief pipe in both the lower and upper layers that enables the water displaced by the air to leave the porous layer and fill a spill tank.
$120 \times 10 \times 290$ mm in which two different sizes of spherical beads (of a diameter 1 and 3 mm) are arranged to create a system of two permeable layers of 3 mm beads, separated by a much less permeable layer, composed of 1 mm beads. This represents an idealised cross-section through an anticline-type feature. Above the upper layer of beads, there is a layer of impermeable putty to prevent air migrating further up the system. There is a pressure relief pipe in both the lower and upper layers that enables the water displaced by the air to leave the porous layer and fill a spill tank.

Figure 9. (a) Schematic of the experimental set-up. (b) Series of frames captured during an experiment with an airflow rate of ![]() $Q=3$ ml s
$Q=3$ ml s![]() $^{-1}$ that illustrate how (i) the plume of air rises at the beginning of the experiment through the lower layer; (ii) a pool of air is formed at the top of the lower layer and gradually deepens; (iii) air breaks through the low permeability layer and rises into the upper layer once the entry pressure has been overcome; (iv,v) a pool of air is formed at the top of the upper layer, while that in the bottom layer tends to an equilibrium depth.
$^{-1}$ that illustrate how (i) the plume of air rises at the beginning of the experiment through the lower layer; (ii) a pool of air is formed at the top of the lower layer and gradually deepens; (iii) air breaks through the low permeability layer and rises into the upper layer once the entry pressure has been overcome; (iv,v) a pool of air is formed at the top of the upper layer, while that in the bottom layer tends to an equilibrium depth.
In each experiment, we initially filled the system with water, which we dyed red to help with visualisation. Air was then injected at a constant rate at the base of the lower layer of high permeability beads. Images of the porous layer showed the pore spaces changed colour from being red to white as the air displaced the water. For example, in figure 9(b) we illustrate a series of images of the bead pack during a typical experiment in which the air gradually accumulated in the lower layer (panels i,ii), and then was able to migrate through the seal layer (panel iii), and a new pool of air accumulated in the upper layer, while the depth of the pool in the lower layer tended to an equilibrium (panels iv,v).
Through digital analysis of the images using Matlab, we measured the area of the bead pack in both the lower and upper layers that changed colour as a function of time. This area includes the plume of air rising through the layer, and the pool of air that collects below the seal. The plume of air, which rises from the nozzle to the pool that accumulates below the seal, has an approximately constant area once it becomes established. The pool of air below the seal steadily increases with time, until air breaks through the seal. In the regions that change colour, the air occupies a fraction ![]() $(1-s))\phi$ of the volume, where
$(1-s))\phi$ of the volume, where ![]() $s$ is the residual saturation of the water and
$s$ is the residual saturation of the water and ![]() $\phi$ is the porosity. We found that
$\phi$ is the porosity. We found that ![]() $(1-s)\phi =0.38 \pm 0.01$ through some independent experiments in which we measured the area that changed colour as air displaced water draining from the cell.
$(1-s)\phi =0.38 \pm 0.01$ through some independent experiments in which we measured the area that changed colour as air displaced water draining from the cell.
In the present experiments, for a range of air supply rates, 1–3 cc s![]() $^{-1}$, we found that the volume of air in the lower layer below the intermediate seal layer at which air began to flow through the intermediate seal layer was
$^{-1}$, we found that the volume of air in the lower layer below the intermediate seal layer at which air began to flow through the intermediate seal layer was ![]() $20 \pm 1.0$ cc, including the plume of air from the supply nozzle to the pool of air, and a pool of air of depth
$20 \pm 1.0$ cc, including the plume of air from the supply nozzle to the pool of air, and a pool of air of depth ![]() $1.5 \pm 0.1$ cm, corresponding to the critical depth required to overcome the capillary entry pressure in the intermediate layer of beads. The vertical distance between the highest and lowest elevation of the base of the seal layer was 5 cm, and so we estimate that
$1.5 \pm 0.1$ cm, corresponding to the critical depth required to overcome the capillary entry pressure in the intermediate layer of beads. The vertical distance between the highest and lowest elevation of the base of the seal layer was 5 cm, and so we estimate that ![]() $P^* = 0.2 \pm 0.02$.
$P^* = 0.2 \pm 0.02$.
In figure 10(a,b) we present measurements of the air volume for two experiments in which air was injected at a rate (b) 1.5 ml s![]() $^{-1}$ and (c) 3.0 ml s
$^{-1}$ and (c) 3.0 ml s![]() $^{-1}$. The figures illustrate the evolution of the volume of air in the lower (black solid) and upper (red solid) layers. In case (a), once the capillary entry pressure is overcome, the system approaches equilibrium in the lower layer, and all the subsequent air migrates into the upper layer. In the experiment with the higher flow rate, figure 10(b), again a pool of air initially develops in the lower layer and this deepens until the buoyancy head overcomes the entry pressure into the seal. Air then flows in the upper layer (red solid line), but with this higher flow rate, the lower pool of air also continues to deepen, as may be seen in the time series of photographs of the lower pool of air for this experiment (figure 10c). When the supply of air at the base of the cell is removed, the depth of the lower pool of air then decreases as the air drains into the upper layer. Eventually the lower layer pool reaches the depth associated with the capillary entry pressure and the drainage to the upper layer ceases (figure 10c).
$^{-1}$. The figures illustrate the evolution of the volume of air in the lower (black solid) and upper (red solid) layers. In case (a), once the capillary entry pressure is overcome, the system approaches equilibrium in the lower layer, and all the subsequent air migrates into the upper layer. In the experiment with the higher flow rate, figure 10(b), again a pool of air initially develops in the lower layer and this deepens until the buoyancy head overcomes the entry pressure into the seal. Air then flows in the upper layer (red solid line), but with this higher flow rate, the lower pool of air also continues to deepen, as may be seen in the time series of photographs of the lower pool of air for this experiment (figure 10c). When the supply of air at the base of the cell is removed, the depth of the lower pool of air then decreases as the air drains into the upper layer. Eventually the lower layer pool reaches the depth associated with the capillary entry pressure and the drainage to the upper layer ceases (figure 10c).

Figure 10. (a,b) Measurements of the volume of air in the lower layer and the upper layer in two experiments with airflow rates (a) ![]() $Q=1.5\ {\rm ml}\ {\rm s}^{-1}$ for
$Q=1.5\ {\rm ml}\ {\rm s}^{-1}$ for ![]() $0< t<35$ s and (b)
$0< t<35$ s and (b) ![]() $Q=3\ {\rm ml}\ {\rm s}^{-1}$ for
$Q=3\ {\rm ml}\ {\rm s}^{-1}$ for ![]() $0< t<20$ s, followed by a period of zero air supply. For each experiment, the volume of air in each layer as measured from the experiments is plotted as a function of time (solid lines), and compared with the predictions of the model (dashed lines). (c) Series of frames captured during the experiment with airflow rate
$0< t<20$ s, followed by a period of zero air supply. For each experiment, the volume of air in each layer as measured from the experiments is plotted as a function of time (solid lines), and compared with the predictions of the model (dashed lines). (c) Series of frames captured during the experiment with airflow rate ![]() $Q=3\ {\rm ml}\ {\rm s}^{-1}$ that illustrate how the pool of air at the top of the lower layer deepens at the beginning of the experiment, then tends to an equilibrium depth, and eventually drains partially once the air supply is turned off.
$Q=3\ {\rm ml}\ {\rm s}^{-1}$ that illustrate how the pool of air at the top of the lower layer deepens at the beginning of the experiment, then tends to an equilibrium depth, and eventually drains partially once the air supply is turned off.
We have adopted the model from the earlier part of the paper, and applied this to the present experiment. In this application of the model we approximate the width of the experimental anticline, ![]() $L(z)$ to be given in terms of the depth,
$L(z)$ to be given in terms of the depth, ![]() $z$, below the apex of the seal layer, as
$z$, below the apex of the seal layer, as ![]() $L(z)=2\beta z$, The volume of air,
$L(z)=2\beta z$, The volume of air, ![]() $V_l$, as a function of depth,
$V_l$, as a function of depth, ![]() $h_l$, follows the relation
$h_l$, follows the relation
where the geometric factor ![]() $\beta = 7/4$ for our experimental cell and
$\beta = 7/4$ for our experimental cell and ![]() $w$ is the width of the cell. Since the cell is not especially wide, in our volume balance we also include the volume of the plume of air,
$w$ is the width of the cell. Since the cell is not especially wide, in our volume balance we also include the volume of the plume of air, ![]() $V_a$, between the injection point and the pool of air below the seal layer. This volume increases until reaching a nearly steady value and the continuing air supply then fills the pool below the seal layer.
$V_a$, between the injection point and the pool of air below the seal layer. This volume increases until reaching a nearly steady value and the continuing air supply then fills the pool below the seal layer.
For air supply ![]() $Q$, the model predicts that the volume of air in the lower layer
$Q$, the model predicts that the volume of air in the lower layer ![]() $V_l$ increases according to the relation
$V_l$ increases according to the relation
when the depth in the lower layer, ![]() $h$, exceeds the capillary entry depth,
$h$, exceeds the capillary entry depth, ![]() $h>h_c$. Here,
$h>h_c$. Here, ![]() $\alpha$ is given by the relation
$\alpha$ is given by the relation ![]() $\alpha = {k w \Delta \rho g \beta / 2 \mu b }$, where
$\alpha = {k w \Delta \rho g \beta / 2 \mu b }$, where ![]() $k$ is the permeability of the partial seal layer of
$k$ is the permeability of the partial seal layer of ![]() $1$ mm beads,
$1$ mm beads, ![]() $\Delta \rho$ is the density of the water,
$\Delta \rho$ is the density of the water, ![]() $g=9.81\ {\rm m}\ {\rm s}^{-2}$,
$g=9.81\ {\rm m}\ {\rm s}^{-2}$, ![]() $\mu = 0.001$ Pa s and
$\mu = 0.001$ Pa s and ![]() $b=2$ cm is the thickness of the partial seal layer. The volume of the upper layer of air,
$b=2$ cm is the thickness of the partial seal layer. The volume of the upper layer of air, ![]() $V_u$, changes as air is supplied according to
$V_u$, changes as air is supplied according to
once ![]() $h>h_c$. In applying the model to the experimental data, for both injection rates shown in figure 10(a,b), we find that
$h>h_c$. In applying the model to the experimental data, for both injection rates shown in figure 10(a,b), we find that ![]() $\alpha$ has a best fit value of
$\alpha$ has a best fit value of ![]() $2.5$, which suggests a permeability of about
$2.5$, which suggests a permeability of about ![]() $9.0 \times 10^{-10}\ {\rm m}^2$. This is comparable to the estimate from the Kozeny–Carman relation for a 1 mm bead pack of
$9.0 \times 10^{-10}\ {\rm m}^2$. This is comparable to the estimate from the Kozeny–Carman relation for a 1 mm bead pack of ![]() $10^{-9}\ {\rm m}^2$. The dimensionless flux of air, for the present experiments, can be defined in a way equivalent to the model, but based on the ratio
$10^{-9}\ {\rm m}^2$. The dimensionless flux of air, for the present experiments, can be defined in a way equivalent to the model, but based on the ratio ![]() $Q^* = Q(supply) / \alpha (H-h_c)^2$ as appropriate for the present experiments. We estimate that
$Q^* = Q(supply) / \alpha (H-h_c)^2$ as appropriate for the present experiments. We estimate that ![]() $Q^*$ has the value
$Q^*$ has the value ![]() $0.05$ and
$0.05$ and ![]() $0.15$ for the two injection rates used in the above experiments.
$0.15$ for the two injection rates used in the above experiments.
The model provides a reasonable fit to the time evolution of the experimental data for two experiments in which the air supply leads to breakthrough and then adjustment to equilibrium of the lower pool of ![]() ${\rm CO}_2$, while a pool develops in the upper layer; the experiments also illustrate the continued leakage from the lower to the upper layer after the air supply is removed (figure 10a,b). Unfortunately, since our experimental system is small, we are unable to explore a very wide range of air injection rates, but the experiments do replicate some of the key processes of filling and drainage identified in the modelling.
${\rm CO}_2$, while a pool develops in the upper layer; the experiments also illustrate the continued leakage from the lower to the upper layer after the air supply is removed (figure 10a,b). Unfortunately, since our experimental system is small, we are unable to explore a very wide range of air injection rates, but the experiments do replicate some of the key processes of filling and drainage identified in the modelling.
6. Application
As an idealised illustration of the model, we now examine the quantitative predictions of the model for representative values of permeability and capillary entry pressure in a subsurface system. We envisage that the ![]() ${\rm CO}_2$ is injected from a line well parallel to a laterally extensive fold, which forms a local two-dimensional anticline-type trap. Observations from the Sleipner field provide some representative values: the mudstone at that field has a capillary entry pressure of order 100 kPa and a typical permeability
${\rm CO}_2$ is injected from a line well parallel to a laterally extensive fold, which forms a local two-dimensional anticline-type trap. Observations from the Sleipner field provide some representative values: the mudstone at that field has a capillary entry pressure of order 100 kPa and a typical permeability ![]() $1\times 10^{-16}\ {\rm m}^2$ (Cavanagh & Haszeldine Reference Cavanagh and Haszeldine2014; Houben et al. Reference Houben, Van Eeden, Barnhoorn and Hangx2020), and so we adopt these values in our present calculation. We assume the fold has a deformation height and layer thickness of
$1\times 10^{-16}\ {\rm m}^2$ (Cavanagh & Haszeldine Reference Cavanagh and Haszeldine2014; Houben et al. Reference Houben, Van Eeden, Barnhoorn and Hangx2020), and so we adopt these values in our present calculation. We assume the fold has a deformation height and layer thickness of ![]() $H = H_{spill} = 50$ m, that the lateral extent of the fold is
$H = H_{spill} = 50$ m, that the lateral extent of the fold is ![]() $2L = 2000$ m, and that the injection well is responsible for the filling of a region of extent 1000 m along the fold,
$2L = 2000$ m, and that the injection well is responsible for the filling of a region of extent 1000 m along the fold, ![]() $d = 1000$ m. Based on the earlier modelling, we find that with this geometry, the maximum storage capacity of the system is about 38 Mt of
$d = 1000$ m. Based on the earlier modelling, we find that with this geometry, the maximum storage capacity of the system is about 38 Mt of ![]() ${\rm CO}_2$ per km along the fold – assuming a
${\rm CO}_2$ per km along the fold – assuming a ![]() ${\rm CO}_2$ density of 550 kg m
${\rm CO}_2$ density of 550 kg m![]() $^{-3}$ and that the storage layer has porosity 0.35. In this arrangement, with a formation permeability in the range
$^{-3}$ and that the storage layer has porosity 0.35. In this arrangement, with a formation permeability in the range ![]() $10^{-12}-10^{-13}\ {\rm m}^2$, a brine density of
$10^{-12}-10^{-13}\ {\rm m}^2$, a brine density of ![]() $1000$ kg m
$1000$ kg m![]() $^{-3}$,
$^{-3}$, ![]() ${\rm CO}_2$ viscosity of
${\rm CO}_2$ viscosity of ![]() $4 \times 10^{-4}$ Pas and mudstone layer thickness of 1 m, we expect the dynamic pressure near each injection point to be much smaller than the buoyancy pressure driving
$4 \times 10^{-4}$ Pas and mudstone layer thickness of 1 m, we expect the dynamic pressure near each injection point to be much smaller than the buoyancy pressure driving ![]() ${\rm CO}_2$ across the mudstone, so that the buoyancy head dominates the well pressure (cf. (1.5)).
${\rm CO}_2$ across the mudstone, so that the buoyancy head dominates the well pressure (cf. (1.5)).
Using these parameters we find that the minimum ![]() ${\rm CO}_2$ depth in the lower layer before it drains into the upper layer is approximately 23 m and the static capacity of the system is about 25 Mt per km along the fold. We now use the model to determine how the
${\rm CO}_2$ depth in the lower layer before it drains into the upper layer is approximately 23 m and the static capacity of the system is about 25 Mt per km along the fold. We now use the model to determine how the ![]() ${\rm CO}_2$ is partitioned between the lower and upper layers for injection at both 1 and 2 Mt year
${\rm CO}_2$ is partitioned between the lower and upper layers for injection at both 1 and 2 Mt year![]() $^{-1}$. In figure 11(a) we show a case with injection at 1 Mt year
$^{-1}$. In figure 11(a) we show a case with injection at 1 Mt year![]() $^{-1}$ and we see that the static capacity is reached after about 24 years of injection. Injection is then stopped and
$^{-1}$ and we see that the static capacity is reached after about 24 years of injection. Injection is then stopped and ![]() ${\rm CO}_2$ continues to drain into the upper layer; the depth of
${\rm CO}_2$ continues to drain into the upper layer; the depth of ![]() ${\rm CO}_2$ in this upper layer asymptotes to a value just smaller than the spill depth. In figure 11(b) we double the injection rate to 2 Mt year
${\rm CO}_2$ in this upper layer asymptotes to a value just smaller than the spill depth. In figure 11(b) we double the injection rate to 2 Mt year![]() $^{-1}$ and see that the lower layer reaches the spill depth before the static capacity is reached. We stop injection after 11.4 years to prevent spilling and we find that 22.8 Mt of
$^{-1}$ and see that the lower layer reaches the spill depth before the static capacity is reached. We stop injection after 11.4 years to prevent spilling and we find that 22.8 Mt of ![]() ${\rm CO}_2$ has been stored.
${\rm CO}_2$ has been stored.

Figure 11. The two panels show the evolution of the depth of ![]() ${\rm CO}_2$ as a function of time in the lower (blue) and upper (red) layers of our example anticline. In both cases we choose a capillary entry pressure of 100 kPa, which is equivalent to a
${\rm CO}_2$ as a function of time in the lower (blue) and upper (red) layers of our example anticline. In both cases we choose a capillary entry pressure of 100 kPa, which is equivalent to a ![]() ${\rm CO}_2$ column of around 23 m. In figure (a) we model an injection rate of 1 Mt year
${\rm CO}_2$ column of around 23 m. In figure (a) we model an injection rate of 1 Mt year![]() $^{-1}$ of
$^{-1}$ of ![]() ${\rm CO}_2$ and find that the static capacity of the system (24.5 Mt per km of anticline) is reached after around 24.5 years of injection. We then stop injection and see that
${\rm CO}_2$ and find that the static capacity of the system (24.5 Mt per km of anticline) is reached after around 24.5 years of injection. We then stop injection and see that ![]() ${\rm CO}_2$ continues to migrate into the upper layer and the depth of
${\rm CO}_2$ continues to migrate into the upper layer and the depth of ![]() ${\rm CO}_2$ in the upper layer will asymptote to the spill depth of 50 m. In figure (b) we model an injection rate of 2 Mt year
${\rm CO}_2$ in the upper layer will asymptote to the spill depth of 50 m. In figure (b) we model an injection rate of 2 Mt year![]() $^{-1}$ of
$^{-1}$ of ![]() ${\rm CO}_2$ and find that the lower layer fills to the spill depth at around 11.4 years of injection, before the static capacity of the system has been reached. This results in a storage of 22.8 Mt, which is approximately 7 % lower than the static capacity. Results are shown for (a) 24.5 Mt
${\rm CO}_2$ and find that the lower layer fills to the spill depth at around 11.4 years of injection, before the static capacity of the system has been reached. This results in a storage of 22.8 Mt, which is approximately 7 % lower than the static capacity. Results are shown for (a) 24.5 Mt ![]() ${\rm CO}_2$ stored and (b) 22.8 Mt
${\rm CO}_2$ stored and (b) 22.8 Mt ![]() ${\rm CO}_2$ stored.
${\rm CO}_2$ stored.
In this example, doubling the injection rate resulted in a 7 % reduction in the mass of ![]() ${\rm CO}_2$ stored to prevent any
${\rm CO}_2$ stored to prevent any ![]() ${\rm CO}_2$ spilling into the aquifer. This identifies the tension in operating such a system between rapid early stage injection, and optimising the long term storage capacity of the system.
${\rm CO}_2$ spilling into the aquifer. This identifies the tension in operating such a system between rapid early stage injection, and optimising the long term storage capacity of the system.
7. Discussion
In this work we have developed a simplified model for the filling dynamics of ![]() ${\rm CO}_2$ injected into a layered anticline system. Our objective was to provide some insights into the static and dynamic controls on the storage potential of a two layer anticline system, with a mudstone separating the two layers. We first illustrated how the static storage capacity of the lower layer is controlled by the geometry and the capillary entry pressure while that of the upper layer is controlled just by the geometry, assuming the overlying formation is fully impermeable. We then illustrated that if the
${\rm CO}_2$ injected into a layered anticline system. Our objective was to provide some insights into the static and dynamic controls on the storage potential of a two layer anticline system, with a mudstone separating the two layers. We first illustrated how the static storage capacity of the lower layer is controlled by the geometry and the capillary entry pressure while that of the upper layer is controlled just by the geometry, assuming the overlying formation is fully impermeable. We then illustrated that if the ![]() ${\rm CO}_2$ is injected into the lower layer, the injection rate compared with the drainage rate across the mudstone is key.
${\rm CO}_2$ is injected into the lower layer, the injection rate compared with the drainage rate across the mudstone is key.
For high injection rates, the lower layer fills and then spills into the adjacent aquifer, and the flux to the upper layer is limited. In this case, if the injection is stopped before any spilling takes place, then the system will not be filled to the static storage capacity. For lower injection rates, the lower layer fills just beyond the depth needed to overcome the capillary entry pressure, and then the ![]() ${\rm CO}_2$ drains into the upper layer. This will eventually fill. If the injection is stopped when the total volume in the layers matches the maximum volume that can be stored in the upper layer plus the equilibrium volume of
${\rm CO}_2$ drains into the upper layer. This will eventually fill. If the injection is stopped when the total volume in the layers matches the maximum volume that can be stored in the upper layer plus the equilibrium volume of ![]() ${\rm CO}_2$ that is capillary trapped in the lower layer, then the system is filled to the maximum static storage capacity. When the injection is stopped, there may be some post-injection drainage if the lower layer has more
${\rm CO}_2$ that is capillary trapped in the lower layer, then the system is filled to the maximum static storage capacity. When the injection is stopped, there may be some post-injection drainage if the lower layer has more ![]() ${\rm CO}_2$ than the equilibrium volume; this will cease once the excess
${\rm CO}_2$ than the equilibrium volume; this will cease once the excess ![]() ${\rm CO}_2$ in the lower layer has drained into the upper layer.
${\rm CO}_2$ in the lower layer has drained into the upper layer.
A series of new experiments in which we injected air into a water-saturated layered bead pack provide support for the model and principles described in the paper.
The model has identified that in order to prevent any spilling into the neighbouring aquifer there is a critical injection rate above which the injected volume is smaller than the maximum static storage volume. This provides a key insight into one of the challenges of filling a carbon storage system. Indeed, it may be necessary to cease injection before either layer is filled to prevent post-injection drainage processes that could cause substantial spillage from the upper layer at the later point.
Funding
The authors wish to thank BP and EPSRC for the award of a CASE studentship funding the research.
Declaration of interests
The authors report no conflict of interest.
Data availability
The data that support the findings of this study are available from the corresponding author on reasonable request.
Appendix A
It is possible to develop the model to account for an axisymmetric anticline system consisting of two layers, ![]() $i=1, 2$, separated by a thin mudstone layer of thickness
$i=1, 2$, separated by a thin mudstone layer of thickness ![]() $b$. Let us assume that the depth of the mud layer above reservoir layer
$b$. Let us assume that the depth of the mud layer above reservoir layer ![]() $1$, relative to the height of the crest of this layer,
$1$, relative to the height of the crest of this layer, ![]() $r=0$, follows a relation of the form
$r=0$, follows a relation of the form ![]() $h_m(r)$. In this case, if the depth of
$h_m(r)$. In this case, if the depth of ![]() ${\rm CO}_2$ below the crest in layer
${\rm CO}_2$ below the crest in layer ![]() $1$ is
$1$ is ![]() $h_1$, then the volume of
$h_1$, then the volume of ![]() ${\rm CO}_2$ in this layer is
${\rm CO}_2$ in this layer is
where ![]() $h_m(r^*)=h_i$. Here, for simplicity, we assume that the seal layer immediately below the reservoir interval
$h_m(r^*)=h_i$. Here, for simplicity, we assume that the seal layer immediately below the reservoir interval ![]() $1$ is deeper than a distance
$1$ is deeper than a distance ![]() $h_1$ below the crest of layer
$h_1$ below the crest of layer ![]() $1$, so the
$1$, so the ![]() ${\rm CO}_2$ in layer
${\rm CO}_2$ in layer ![]() $1$ does not intersect the lower seal layer.
$1$ does not intersect the lower seal layer.
If the capillary entry pressure across the mud layer is equivalent to a depth ![]() $h_c$, then if
$h_c$, then if ![]() $h_1 > h_c$, there will be some flow through the mudstone into the overlying reservoir layer 2, in the region
$h_1 > h_c$, there will be some flow through the mudstone into the overlying reservoir layer 2, in the region ![]() $0< r< r^{**}$, where
$0< r< r^{**}$, where ![]() $h_m(r^{**})= h_1-h_c$. The flux is given by
$h_m(r^{**})= h_1-h_c$. The flux is given by
With these relations, we can calculate the rate of deepening of the ![]() ${\rm CO}_2$ at the top of layer
${\rm CO}_2$ at the top of layer ![]() $1$,
$1$,
where ![]() $Q_o$ is the supply of
$Q_o$ is the supply of ![]() ${\rm CO}_2$ to layer
${\rm CO}_2$ to layer ![]() $1$, and the flux that leaks through the mudstone into the overlying layer is
$1$, and the flux that leaks through the mudstone into the overlying layer is ![]() $Q_l$. We now combine this with the flow in the overlying layer, of volume
$Q_l$. We now combine this with the flow in the overlying layer, of volume ![]() $V_2$ say,
$V_2$ say,
If this upper layer is bounded above by a fully sealing layer, then we have a model for an axisymmetric two layer anticline system, analogous to the model developed in the paper. Other developments of the model for the axisymmetric problem follow in a similar fashion.