Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-27T01:54:13.071Z Has data issue: false hasContentIssue false
  • English
  • Français

Distorted turbulence and secondary flow near right-angled plates

Published online by Cambridge University Press:  16 December 2010

K. NAGATA ,
J. C. R. HUNT ,
Y. SAKAI  and
H. WONG
K. NAGATA*
Affiliation:
Department of Mechanical Science and Engineering, Nagoya University, Nagoya 464-8603, Japan
J. C. R. HUNT
Affiliation:
Department of Earth Science, University College London, London WC1E 6BT, UK
Y. SAKAI
Affiliation:
Department of Mechanical Science and Engineering, Nagoya University, Nagoya 464-8603, Japan
H. WONG
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Cambridge CB3 9EW, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In many turbulent flows near obstacles or in ducts, the turbulence is inhomogeneous in two directions perpendicular to the main flow direction. In convective flows, there may initially be no mean motion. In both types of flow the gradients of Reynolds stresses drive mean motions in directions of inhomogeneity. Using the method of rapid distortion theory developed by Hunt & Graham (J. Fluid Mech., vol. 84, 1978, p. 209), we analyse these gradients where homogeneous isotropic turbulence is impinging onto two semi-infinite flat rigid surfaces intersecting at right angles. The mean velocity is assumed to be uniform (i.e. the surfaces move at free-stream velocity, or the boundary layers are very thin). The inhomogeneous spectra, variances and Reynolds-stress gradients are evaluated. For isotropic free-stream turbulence with mean square velocity u2∞1, the mean square velocity fluctuation at a high Reynolds number in the corner is u21(X, 0, 0) = 2.121u2∞1, independent of the form of the spectrum. This is explained by estimating how the free-stream eddies are blocked by the two walls. The gradients of Reynolds stresses force a mean secondary flow to develop; its direction is into the corner, and its magnitude at time t is of order tu2∞1/L∞, where L∞ is the integral scale. These results are tested in a wind tunnel experiment. A turbulence-generating grid installed at the entrance to the test section generates nearly isotropic, grid-generated turbulence. A corner plate with faces parallel to the mean flow and sharp edges is placed downstream of the grid so that shear-free turbulence impinges onto the corner plate. The turbulent Reynolds number based on 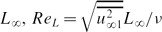, is 1400 at the leading edge of the plate. A hot-wire anemometry is used to measure instantaneous velocities. The experimental results are consistent with the rapid distortion theory estimates for the variances and the secondary mean motion, which is in the same direction and has the same order of magnitude as Prandtl's analysis of shear-driven secondary flow (of the second kind). We conclude that the blocking mechanism adds to the shear effects and has a significant and sometimes dominant contribution to the crossflows wherever it acts in two non-parallel directions, such as convection in a corner. Consequently, mean transport into corners occurs for most kinds of distorted flow with weak viscous stresses, which has many engineering and environmental implications. There are also implications for the chaotic nature of many confined flows near corners.

JFM classification

Turbulent Flows: Turbulence theory Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 668 , 10 February 2011 , pp. 446 - 479
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: European Space Agency and AOES, Haagse Schouwweg 6G, Leiden, The Netherlands

References

REFERENCES

Bagnold, R. A. 1941 The Physics of Blown Sand and Desert Dunes. Chapman & Hall.Google Scholar
Batchelor, G. K. 1953 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
Bradshaw, P. 1987 Turbulent secondary flows. Annu. Rev. Fluid Mech. 19, 53–74.CrossRefGoogle Scholar
Brundrett, E. & Baines, W. D. 1964 The production and dissipation of vorticity in duct flow. J. Fluid Mech. 19, 375–394.CrossRefGoogle Scholar
Colombini, M. 1993 Turbulence-driven secondary flows and formation of sand ridges. J. Fluid Mech. 254, 701–719.CrossRefGoogle Scholar
Comte-Bellot, G. & Corrsin, S. 1971 Simple Eulerian time correlation of full- and narrow-band velocity signals in grid-generated ‘isotropic’ turbulence. J. Fluid Mech. 48 (2), 273–337.CrossRefGoogle Scholar
Demuren, A. O. & Rodi, W. 1984 Calculation of turbulence-driven secondary motion in non-circular ducts. J. Fluid Mech. 140, 189–222.CrossRefGoogle Scholar
Durbin, P. A. & Pettersson Reif, B. A. 2001 Statistical Theory and Modeling for Turbulent Flows. Wiley.Google Scholar
Einstein, H. A. & Li, H. 1958 Secondary currents in straight channels. Trans. Am. Geophys. Union 39, 1085–1088.Google Scholar
Fernando, H. J. S. & De Silva, I. P. D. 1993 Note on secondary flows in oscillating-grid, mixing-box experiments. Phys. Fluids A 5 (7), 1849–1851.CrossRefGoogle Scholar
Gavrilakis, S. 1992 Numerical simulation of low-Reynolds-number turbulent flow through a straight square duct. J. Fluid Mech. 244, 101–129.CrossRefGoogle Scholar
Gessner, F. B. 1973 The origin of secondary flow in turbulent flow along a corner. J. Fluid Mech. 58 (1), 1–25.CrossRefGoogle Scholar
Gessner, F. B. & Emery, A. F. 1981 The numerical prediction of developing turbulent flow in rectangular ducts. J. Fluids Engng 103 (3), 445–453.CrossRefGoogle Scholar
Gessner, F. B. & Jones, J. B. 1965 On some aspects of fully-developed turbulent flow in rectangular channels. J. Fluid Mech. 23, 689–713.CrossRefGoogle Scholar
Hunt, J. C. R. 1968 A uniqueness theorem for magnetohydrodynamic duct flows. Proc. Camb. Phil. Soc. 65, 319–328.CrossRefGoogle Scholar
Hunt, J. C. R. 1973 A theory of turbulent flow round two-dimensional bluff bodies. J. Fluid Mech. 61, 625–706.CrossRefGoogle Scholar
Hunt, J. C. R. 1984 Turbulence structure in thermal convection and shear-free boundary layers. J. Fluid Mech. 138, 161–184.CrossRefGoogle Scholar
Hunt, J. C. R. & Carlotti, P. 2001 Statistical structure at the wall of the high Reynolds number turbulent boundary layer. Flow Turbul. Combust. 66, 453–475.CrossRefGoogle Scholar
Hunt, J. C. R. & Carruthers, D. J. 1990 Rapid distortion theory and the ‘problems’ of turbulence. J. Fluid Mech. 212, 497–532.CrossRefGoogle Scholar
Hunt, J. C. R. & Graham, J. M. R. 1978 Free-stream turbulence near plane boundaries. J. Fluid Mech. 84, 209–235.CrossRefGoogle Scholar
Hunt, J. C. R., Moin, P., Lee, M., Moser, R. D., Spalart, P., Mansour, N. N., Kaimal, J. C. & Gaynor, E. 1989 Cross correlation and length scales in turbulent flows near surfaces. Adv. Turbul. 2, 128–134.CrossRefGoogle Scholar
Hunt, J. C. R. & Morrison, J. F. 2000 Eddy structure in turbulent boundary layers. Eur. J. Mech. B – Fluids 19, 673–694.CrossRefGoogle Scholar
Jayesh, Yoon K. & Warhaft, Z. 1990 Turbulent mixing and transport in a thermally stratified interfacial layer in decaying grid turbulence. Phys. Fluids A 3 (5), 1143–1155.CrossRefGoogle Scholar
Jones, W. P. & Launder, B. E. 1972 Some properties of sink-flow turbulent boundary layer. J. Fluid Mech. 56, 337–351.CrossRefGoogle Scholar
Kadanoff, L. P. 1994 Conditional averages in convective turbulence. Physica A 204, 341–345.CrossRefGoogle Scholar
Launder, B. E., Reece, G. J. & Rodi, W. 1975 Progress in the development of a Reynolds-stress turbulence closure. J. Fluid Mech. 68, 537–566.CrossRefGoogle Scholar
Launder, B. E. & Ying, W. M. 1973 Prediction of flow and heat transfer in ducts of square cross-section. Proc. Inst. Mech. Engng 187, 455–461.CrossRefGoogle Scholar
Lumley, J. L. 2001 Early work on fluid mechanics in the IC engine. Annu. Rev. Fluid Mech. 33, 319–338.CrossRefGoogle Scholar
Magnaudet, J. 2003 High-Reynolds-number turbulence in a shear-free boundary layer: revisiting the Hunt–Graham theory. J. Fluid Mech. 484, 167–196.CrossRefGoogle Scholar
McKenna, S. P. & McGillis, W. R. 2004 Observations of flow repeatability and secondary circulation in an oscillating grid-stirred tank. Phys. Fluids 16 (9), 3499–3502.CrossRefGoogle Scholar
Moffatt, H. K. 1964 Viscous and resistive eddies near a sharp corner. J. Fluid Mech. 18, 1–18.CrossRefGoogle Scholar
Nagata, K., Wong, H., Hunt, J. C. R., Sajjadi, S. G. & Davidson, P. A. 2006 Weak mean flows induced by anisotropic turbulence impinging onto planar and undulating surfaces. J. Fluid Mech. 556, 329–360.CrossRefGoogle Scholar
Nakamura, I., Sakai, Y. & Miyata, M. 1987 Diffusion of matter by a non-buoyant plume in grid-generated turbulence. J. Fluid Mech. 178, 379–403.CrossRefGoogle Scholar
Perkins, H. J. 1970 The formation of streamwise vorticity in turbulent flow. J. Fluid Mech. 44 (4), 721–740.CrossRefGoogle Scholar
Perot, B. & Moin, P. 1995 Shear-free turbulent boundary layers. Part 1. Physical insights into near-wall turbulence. J. Fluid Mech. 295, 199–227.CrossRefGoogle Scholar
Prandtl, L. 1952 Essentials of Fluid Dynamics. Dover.Google Scholar
Rubin, S. G. 1966 Incompressible flow along a corner. J. Fluid Mech. 26, 97–110.CrossRefGoogle Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Tsai, Y. S., Hunt, J. C. R., Niewstadt, F. T. M., Westerweel, J. & Gunasekaran, B. P. N. 2007 Effect of strong external turbulence on a wall jet boundary layer. Flow Turbul. Combust. 79 (3), 155–174.CrossRefGoogle Scholar
Warhaft, Z. & Lumley, J. L. 1978 An experimental study of the decay of temperature fluctuations in grid-generated turbulence. J. Fluid Mech. 88, 659–684.CrossRefGoogle Scholar
Wong, H. Y. W. 1985 Shear-free turbulence and secondary flow near angled and curved surfaces. PhD Thesis, University of Cambridge, Cambridge, UK.Google Scholar
Zhou, T. & Antonia, R. A. 2000 Reynolds number dependence of the small-scale structure of grid turbulence. J. Fluid Mech. 406, 81–107.CrossRefGoogle Scholar