Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-24T11:31:35.791Z Has data issue: false hasContentIssue false
  • English
  • Français

Dispersion in the large-deviation regime. Part 1: shear flows and periodic flows

Published online by Cambridge University Press:  19 March 2014

P. H. Haynes  and
J. Vanneste
P. H. Haynes
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
J. Vanneste*
Affiliation:
School of Mathematics and Maxwell Institute for Mathematical Sciences, University of Edinburgh, King’s Buildings, Edinburgh EH9 3JZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The dispersion of a passive scalar in a fluid through the combined action of advection and molecular diffusion is often described as a diffusive process, with an effective diffusivity that is enhanced compared with the molecular value. However, this description fails to capture the tails of the scalar concentration distribution in initial-value problems. To remedy this, we develop a large-deviation theory of scalar dispersion that provides an approximation to the scalar concentration valid at much larger distances away from the centre of mass, specifically distances that are 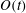$O(t)$ rather than 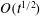$O(t^{1/2})$, where 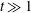$t \gg 1$ is the time from the scalar release. The theory centres on the calculation of a rate function characterizing the large-time form of the scalar concentration. This function is deduced from the solution of a one-parameter family of eigenvalue problems which we derive using two alternative approaches, one asymptotic, the other probabilistic. We emphasize the connection between the large-deviation theory and the homogenization theory that is often used to compute effective diffusivities: a perturbative solution of the eigenvalue problems in the appropriate limit reduces at leading order to the cell problem of homogenization theory. We consider two classes of flows in some detail: shear flows and periodic flows with closed streamlines (cellular flows). In both cases, large deviation generalizes classical results on effective diffusivity and captures new phenomena relevant to the tails of the scalar distribution. These include approximately finite dispersion speeds arising at large Péclet number 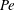$\mathit{Pe}$ (corresponding to small molecular diffusivity) and, for two-dimensional cellular flows, anisotropic dispersion. Explicit asymptotic results are obtained for shear flows in the limit of large 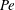$\mathit{Pe}$. (A companion paper, Part 2, is devoted to the large-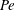$\mathit{Pe}$ asymptotic treatment of cellular flows.) The predictions of large-deviation theory are compared with Monte Carlo simulations that estimate the tails of concentration accurately using importance sampling.

JFM classification

Mixing: Chaotic advection Reacting Flows: Laminar reacting flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 745 , 25 April 2014 , pp. 321 - 350
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aris, R. 1956 On the dispersion of a solute in a fluid flowing through a tube. Proc. R. Soc. Lond. A 235, 67–76.Google Scholar
Bensoussan, A., Lions, J. L. & Papanicolaou, G. C. 1989 Asymptotic Analysis of Periodic Structures. Kluwer.Google Scholar
Berestycki, H., Nirenberg, L. & Varadhan, S. R. S. 1994 The principal eigenvalue and maximum principle for second-order elliptic operators in general domains. Commun. Pure Appl. Maths 47, 47–92.Google Scholar
Camassa, R., Lin, Z. & McLaughlin, R. M. 2010 The exact solution of the scalar variance in pipe and channel flow. Commun. Math. Sci. 8, 601–626.CrossRefGoogle Scholar
Chatwin, P. C. 1970 The approach to normality of the concentration distribution of a solute flowing along a straight pipe. J. Fluid Mech. 43, 321–352.Google Scholar
Chatwin, P. C. 1972 The cumulants of the distribution of concentration of a solute dispersing in solvent flowing through a tube. J. Fluid Mech. 51, 63–67.Google Scholar
Childress, S. 1979 Alpha-effect in flux ropes and sheets. Phys. Earth Planet. Inter. 20, 172–180.Google Scholar
Dembo, A. & Zeitouni, O. 1998 Large Deviations: Techniques and Applications. Springer.Google Scholar
den Hollander, F.2000 Large Deviations, Fields Institute Monographs, American Mathematical Society.Google Scholar
Ellis, R. S. 1995 An overview of the theory of large deviations and applications to statistical physics. Actuar. J. 1, 97–142.Google Scholar
Freidlin, M. 1985 Functional Integration and Partial Differential Equations. Princeton University Press.Google Scholar
Freidlin, M. & Wentzell, A. 2012 Random Perturbations of Dynamical Systems. 3rd edn. Springer.Google Scholar
Gardiner, C. W. 2004 Handbook of Stochastic Methods. 3rd edn. Springer.CrossRefGoogle Scholar
Gärtner, J. & Freidlin, M. I. 1979 The propagation of concentration waves in periodic and random media. Sov. Math. Dokl. 20, 1282–1286.Google Scholar
Gorb, Y., Nam, D. & Novikov, A. 2011 Numerical simulations of diffusion in cellular flows at high Péclet number. Discrete Continuous Dyn. Syst. B 15, 75–92.Google Scholar
Grassberger, P. 1997 Prune-enriched Rosenbluth method: simulations of $\theta $ polymers of chains length up to 1 000 000. Phys. Rev. E 56, 3682–3693.Google Scholar
Grassberger, P. 2002 Go with the winners: a general Monte Carlo strategy. Comput. Phys. Commun. 147, 64–70.Google Scholar
Haynes, P. H. & Vanneste, J. 2014 Dispersion in the large-deviation regime. Part 2. Cellular flow at large Péclet number. J. Fluid Mech. 745, 351–377.Google Scholar
Jansons, K. M. & Rogers, L. C. G. 1995 Probability and dispersion theory. IMA J. Appl. Maths. 55, 149–162.Google Scholar
Keller, J. B. 2004 Diffusion at finite speed and random walks. Proc. Natl Acad. Sci. USA 101, 1120–1122.Google Scholar
Kuske, R. & Keller, J. B. 1997 Large deviation theory for stochastic difference equations. Eur. J. Appl. Maths 8, 567–580.Google Scholar
Majda, A. J. & Kramer, P. R. 1999 Simplified models for turbulent diffusion: theory, numerical modelling and physical phenomena. Phys. Rep. 314, 237–574.Google Scholar
Mercer, G. N. & Roberts, A. J. 1990 A centre manifold description of contaminant dispersion in channels with varying flow properties. SIAM J. Appl. Maths 50, 1547–1565.Google Scholar
Milstein, G. N. 1995 Numerical Solution of Stochastic Differential Equations. Kluwer.Google Scholar
Moffatt, H. K. 1983 Transport effects associated with turbulence with particular attention to the influence of helicity. Rep. Prog. Phys. 46, 621–664.CrossRefGoogle Scholar
Novikov, A., Papanicolaou, G. & Ryzhik, L. 2005 Boundary layers for cellular flows at high Péclet numbers. Commun. Pure Appl. Maths 867–922, 563–580.Google Scholar
Øksendal, B. 1998 Stochastic Differential Equations. Springer.Google Scholar
Papanicolaou, G. C. 1995 Diffusion in Random Media. In Surveys in Applied Mathematics (ed. Keller, J. P.), vol. 1, pp. 205–253. Plenum.Google Scholar
Pavliotis, G. A. & Stuart, A. M. 2007 Multiscale Methods: Averaging and Homogenization. Springer.Google Scholar
Rosenbluth, M. N., Berk, H. L., Doxas, I. & Horton, W. 1987 Effective diffusion in laminar convective flows. Phys. Fluids 30, 2636–2647.Google Scholar
Sagues, F. & Horsthemke, W. 1986 Diffusive transport in spatially periodic hydrodynamic flows. Phys. Rev. A 34, 4136–4143.CrossRefGoogle ScholarPubMed
Shraiman, B. I. 1987 Diffusive transport in a Rayleigh–Bénard convection cell. Phys. Rev. A 36, 261–267.Google Scholar
Simon, B. 1983 Semiclassical analysis of low lying eigenvalues. I. Non-degenerate minima: asymptotic expansions. Ann. Inst. Henri Poincaré 38, 295–307.Google Scholar
Soward, A. M. 1987 Fast dynamo action in a steady flow. J. Fluid Mech. 180, 267–295.Google Scholar
Tailleur, J. & Kurchan, J. 2007 Probing rare physical trajectories with Lyapunov-weighted dynamics. Nat. Phys. 3, 203–207.Google Scholar
Taylor, G. I. 1953 Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond. A 219, 186–203.Google Scholar
Touchette, H. 2009 Large deviation approach to statistical mechanics. Phys. Rep. 478, 1–69.Google Scholar
Tzella, A. & Vanneste, J.2014a Front propagation in cellular flows: a large-deviation approach (in preparation).Google Scholar
Tzella, A. & Vanneste, J.2014b Front propagation in cellular flows for fast reaction and small diffusivity (in preparation).Google Scholar
Vanneste, J. 2010 Estimating generalized Lyapunov exponents for products of random matrices. Phys. Rev. E 81, 036701.Google Scholar
Xin, J. 2009 An Introduction to Fronts in Random Media. Springer.Google Scholar
Young, W. R. & Jones, S. 1991 Shear dispersion. Phys. Fluids A3, 1087–1101.Google Scholar
Zauderer, E. 2009 Partial Differential Equations of Applied Mathematics. 3rd edn. John Wiley & Sons.Google Scholar