Published online by Cambridge University Press: 13 September 2016
Turbulent heat transfer across a sheared wind-driven gas–liquid interface is investigated by means of a direct numerical simulation of gas–liquid two-phase turbulent flows under non-breaking wave conditions. The wind-driven wavy gas–liquid interface is captured using the arbitrary Lagrangian–Eulerian method with boundary-fitted coordinates on moving grids, and the temperature fields on both the gas and liquid sides, and the humidity field on the gas side are solved. The results show that although the distributions of the total, latent, sensible and radiative heat fluxes at the gas–liquid interface exhibit streak features such that low-heat-flux regions correspond to both low-streamwise-velocity regions on the gas side and high-streamwise-velocity regions on the liquid side, the similarity between the heat-flux streak and velocity streak on the gas side is more significant than that on the liquid side. This means that, under the condition of a fully developed wind-driven turbulent field on both the gas and liquid sides, the heat transfer across the sheared wind-driven gas–liquid interface is strongly affected by the turbulent eddies on the gas side, rather than by the turbulent eddies and Langmuir circulations on the liquid side. This trend is quite different from that of the mass transfer (i.e. 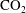 $\text{CO}_{2}$ gas). This is because the resistance to heat transfer is normally lower than the resistance to mass transfer on the liquid side, and therefore the heat transfer is controlled by the turbulent eddies on the gas side. It is also verified that the predicted total heat, latent heat, sensible heat and enthalpy transfer coefficients agree well with previously measured values in both laboratory and field experiments. To estimate the heat transfer coefficients on both the gas and liquid sides, the surface divergence could be a useful parameter, even when Langmuir circulations exist.
$\text{CO}_{2}$ gas). This is because the resistance to heat transfer is normally lower than the resistance to mass transfer on the liquid side, and therefore the heat transfer is controlled by the turbulent eddies on the gas side. It is also verified that the predicted total heat, latent heat, sensible heat and enthalpy transfer coefficients agree well with previously measured values in both laboratory and field experiments. To estimate the heat transfer coefficients on both the gas and liquid sides, the surface divergence could be a useful parameter, even when Langmuir circulations exist.