Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Pathikonda, Gokul
and
Christensen, Kenneth T.
2017.
Inner–outer interactions in a turbulent boundary layer overlying complex roughness.
Physical Review Fluids,
Vol. 2,
Issue. 4,
Chan, L.
MacDonald, M.
Chung, D.
Hutchins, N.
and
Ooi, A.
2018.
Secondary motion in turbulent pipe flow with three-dimensional roughness.
Journal of Fluid Mechanics,
Vol. 854,
Issue. ,
p.
5.
Murphy, Elizabeth A. K.
Barros, Julio M.
Schultz, Michael P.
Flack, Karen A.
Steppe, Cecily N.
and
Reidenbach, Matthew A.
2018.
Roughness effects of diatomaceous slime fouling on turbulent boundary layer hydrodynamics.
Biofouling,
Vol. 34,
Issue. 9,
p.
976.
Barros, Julio M.
Schultz, Michael P.
and
Flack, Karen A.
2018.
Measurements of skin-friction of systematically generated surface roughness.
International Journal of Heat and Fluid Flow,
Vol. 72,
Issue. ,
p.
1.
Medjnoun, T.
Vanderwel, C.
and
Ganapathisubramani, B.
2018.
Characteristics of turbulent boundary layers over smooth surfaces with spanwise heterogeneities.
Journal of Fluid Mechanics,
Vol. 838,
Issue. ,
p.
516.
Bai, H. L.
Kevin
Hutchins, N.
and
Monty, J. P.
2018.
Turbulence modifications in a turbulent boundary layer over a rough wall with spanwise-alternating roughness strips.
Physics of Fluids,
Vol. 30,
Issue. 5,
Ni, Weidan
Lu, Lipeng
Fang, Jian
Moulinec, Charles
and
Yao, Yufeng
2018.
Large-Scale Streamwise Vortices in Turbulent Channel Flow Induced by Active Wall Actuations.
Flow, Turbulence and Combustion,
Vol. 100,
Issue. 3,
p.
651.
Xu, Fang
Zhong, Shan
and
Zhang, Shanying
2018.
Vortical structures and development of laminar flow over convergent-divergent riblets.
Physics of Fluids,
Vol. 30,
Issue. 5,
Silvestri, Anton
Ghanadi, Farzin
Arjomandi, Maziar
Cazzolato, Benjamin
Zander, Anthony
and
Chin, Rey
2018.
Mechanism of sweep event attenuation using micro-cavities in a turbulent boundary layer.
Physics of Fluids,
Vol. 30,
Issue. 5,
Meyers, Johan
Ganapathisubramani, Bharathram
and
Cal, Raúl Bayoán
2019.
On the decay of dispersive motions in the outer region of rough-wall boundary layers.
Journal of Fluid Mechanics,
Vol. 862,
Issue. ,
Anderson, W.
2019.
Non-periodic phase-space trajectories of roughness-driven secondary flows in high- boundary layers and channels.
Journal of Fluid Mechanics,
Vol. 869,
Issue. ,
p.
27.
Ni, Weidan
Lu, Lipeng
Fang, Jian
Moulinec, Charles
Emerson, David R.
and
Yao, Yufeng
2019.
Flow separation control over a rounded ramp with spanwise alternating wall actuation.
Physics of Fluids,
Vol. 31,
Issue. 1,
Liu, Qiang
Zhong, Shan
and
Li, Lin
2019.
Effects of Bio-Inspired Micro-Scale Surface Patterns on the Profile Losses in a Linear Cascade.
Journal of Turbomachinery,
Vol. 141,
Issue. 12,
Jiansheng, Wang
Yu, Jiao
and
Xueling, Liu
2019.
Heat transfer and flow characteristics in a rectangular channel with small scale vortex generators.
International Journal of Heat and Mass Transfer,
Vol. 138,
Issue. ,
p.
208.
Kevin, Kevin
Monty, Jason
and
Hutchins, Nicholas
2019.
The meandering behaviour of large-scale structures in turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 865,
Issue. ,
Vanderwel, C.
Stroh, A.
Kriegseis, J.
Frohnapfel, B.
and
Ganapathisubramani, B.
2019.
The instantaneous structure of secondary flows in turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 862,
Issue. ,
p.
845.
Kevin, Kevin
Monty, Jason
and
Hutchins, Nicholas
2019.
Turbulent structures in a statistically three-dimensional boundary layer.
Journal of Fluid Mechanics,
Vol. 859,
Issue. ,
p.
543.
Xu, Fang
Zhong, Shan
and
Zhang, Shanying
2019.
Statistical analysis of vortical structures in turbulent boundary layer over directional grooved surface pattern with spanwise heterogeneity.
Physics of Fluids,
Vol. 31,
Issue. 8,
Lin, L. M.
and
Wu, Y. X.
2020.
Mechanism for vorticity in a secondary flow within a pipe: Vortex-induced vortex.
Physics of Fluids,
Vol. 32,
Issue. 3,
Medjnoun, T.
Vanderwel, C.
and
Ganapathisubramani, B.
2020.
Effects of heterogeneous surface geometry on secondary flows in turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 886,
Issue. ,
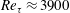 $Re_{\unicode[STIX]{x1D70F}}\approx 3900$. The three velocity components resulting from this experiment reveal a pronounced spanwise periodicity in all single-point velocity statistics. Consistent with previous hot-wire studies over similar-type riblets, we observe a weak time-average secondary flow in the form of
$Re_{\unicode[STIX]{x1D70F}}\approx 3900$. The three velocity components resulting from this experiment reveal a pronounced spanwise periodicity in all single-point velocity statistics. Consistent with previous hot-wire studies over similar-type riblets, we observe a weak time-average secondary flow in the form of 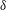 $\unicode[STIX]{x1D6FF}$-filling streamwise vortices. The observed differences in the surface and secondary flow characteristics, compared to other heterogeneous-roughness studies, may suggest that different mechanisms are responsible for the flow modifications in this case. Observations of instantaneous velocity fields reveal modified and rearranged turbulence structures. The instantaneous snapshots also suggest that the time-average secondary flow may be an artefact arising from superpositions of much stronger instantaneous turbulent events enhanced by the surface texture. In addition, the observed instantaneous secondary motions seem to have promoted a free-stream-engulfing behaviour in the outer layer, which would indicate an increase turbulent/non-turbulent flow mixing. It is overall demonstrated that the presence of large-scale directionality in transitional surface roughness can cause a modification throughout the entire boundary layer, even when the roughness height is 0.5 % of the layer thickness.
$\unicode[STIX]{x1D6FF}$-filling streamwise vortices. The observed differences in the surface and secondary flow characteristics, compared to other heterogeneous-roughness studies, may suggest that different mechanisms are responsible for the flow modifications in this case. Observations of instantaneous velocity fields reveal modified and rearranged turbulence structures. The instantaneous snapshots also suggest that the time-average secondary flow may be an artefact arising from superpositions of much stronger instantaneous turbulent events enhanced by the surface texture. In addition, the observed instantaneous secondary motions seem to have promoted a free-stream-engulfing behaviour in the outer layer, which would indicate an increase turbulent/non-turbulent flow mixing. It is overall demonstrated that the presence of large-scale directionality in transitional surface roughness can cause a modification throughout the entire boundary layer, even when the roughness height is 0.5 % of the layer thickness.