Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Thiesset, F.
Schaeffer, V.
Djenidi, L.
and
Antonia, R. A.
2014.
On self-preservation and log-similarity in a slightly heated axisymmetric mixing layer.
Physics of Fluids,
Vol. 26,
Issue. 7,
Tang, S. L.
Antonia, R. A.
Djenidi, L.
Abe, H.
Zhou, T.
Danaila, L.
and
Zhou, Y.
2015.
Transport equation for the mean turbulent energy dissipation rate on the centreline of a fully developed channel flow.
Journal of Fluid Mechanics,
Vol. 777,
Issue. ,
p.
151.
Darisse, Alexis
Lemay, Jean
and
Benaïssa, Azemi
2015.
Budgets of turbulent kinetic energy, Reynolds stresses, variance of temperature fluctuations and turbulent heat fluxes in a round jet.
Journal of Fluid Mechanics,
Vol. 774,
Issue. ,
p.
95.
Tang, S. L.
Antonia, R. A.
Djenidi, L.
and
Zhou, Y.
2015.
Transport equation for the isotropic turbulent energy dissipation rate in the far-wake of a circular cylinder.
Journal of Fluid Mechanics,
Vol. 784,
Issue. ,
p.
109.
Antonia, R. A.
Tang, S. L.
Djenidi, L.
and
Danaila, L.
2015.
Boundedness of the velocity derivative skewness in various turbulent flows.
Journal of Fluid Mechanics,
Vol. 781,
Issue. ,
p.
727.
Sadeghi, Hamed
Lavoie, Philippe
and
Pollard, Andrew
2016.
Scale-by-scale budget equation and its self-preservation in the shear-layer of a free round jet.
International Journal of Heat and Fluid Flow,
Vol. 61,
Issue. ,
p.
85.
Tang, S. L.
Antonia, R. A.
Djenidi, L.
Danaila, L.
and
Zhou, Y.
2016.
Boundedness of the mixed velocity-temperature derivative skewness in homogeneous isotropic turbulence.
Physics of Fluids,
Vol. 28,
Issue. 9,
Djenidi, L.
Antonia, R. A.
Lefeuvre, N.
and
Lemay, J.
2016.
Complete self-preservation on the axis of a turbulent round jet.
Journal of Fluid Mechanics,
Vol. 790,
Issue. ,
p.
57.
Tang, S. L.
Antonia, R. A.
Djenidi, L.
and
Zhou, Y.
2016.
Complete self-preservation along the axis of a circular cylinder far wake.
Journal of Fluid Mechanics,
Vol. 786,
Issue. ,
p.
253.
Djenidi, L.
Lefeuvre, N.
Kamruzzaman, M.
and
Antonia, R. A.
2017.
On the normalized dissipation parameter in decaying turbulence.
Journal of Fluid Mechanics,
Vol. 817,
Issue. ,
p.
61.
Tang, S. L.
Antonia, R. A.
Djenidi, L.
Danaila, L.
and
Zhou, Y.
2017.
Finite Reynolds number effect on the scaling range behaviour of turbulent longitudinal velocity structure functions.
Journal of Fluid Mechanics,
Vol. 820,
Issue. ,
p.
341.
Antonia, R. A.
Djenidi, L.
Danaila, L.
and
Tang, S. L.
2017.
Small scale turbulence and the finite Reynolds number effect.
Physics of Fluids,
Vol. 29,
Issue. 2,
Lavoie, P.
Pollard, A.
and
Sadeghi, H.
2017.
Whither Turbulence and Big Data in the 21st Century?.
p.
119.
Breda, Massimiliano
and
Buxton, Oliver R. H.
2018.
Influence of coherent structures on the evolution of an axisymmetric turbulent jet.
Physics of Fluids,
Vol. 30,
Issue. 3,
2018.
Retraction 17-00374.
Mechanical Engineering Reviews,
Vol. 5,
Issue. 1,
p.
17-00374.
Tang, S. L.
Antonia, R. A.
Djenidi, L.
Danaila, L.
and
Zhou, Y.
2018.
Reappraisal of the velocity derivative flatness factor in various turbulent flows.
Journal of Fluid Mechanics,
Vol. 847,
Issue. ,
p.
244.
Das, Niloy
Islam, S. M. Rakibul
Mohammed, Sayeed
and
Hasan, Mohammad Nasim
2018.
Numerical study of turbulent round free jet.
Vol. 1983,
Issue. ,
p.
040026.
Antonia, R. A.
Tang, S. L.
Djenidi, L.
and
Zhou, Y.
2019.
Finite Reynolds number effect and the 4/5 law.
Physical Review Fluids,
Vol. 4,
Issue. 8,
Djenidi, L.
Antonia, R. A.
and
Tang, S. L.
2019.
Scale invariance in finite Reynolds number homogeneous isotropic turbulence.
Journal of Fluid Mechanics,
Vol. 864,
Issue. ,
p.
244.
Bouha, A.
Varea, E.
Patte-Rouland, B.
and
Danaila, L.
2019.
Turbulent Cascades II.
Vol. 26,
Issue. ,
p.
145.
 $\overline{\epsilon }$ and the longitudinal velocity variance
$\overline{\epsilon }$ and the longitudinal velocity variance 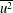 $\overline{u^2}$ on the axis of a round jet are derived. In particular, the prefactor for
$\overline{u^2}$ on the axis of a round jet are derived. In particular, the prefactor for 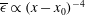 $\overline{\epsilon } \propto (x-x_0)^{-4}$, where
$\overline{\epsilon } \propto (x-x_0)^{-4}$, where 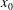 $x_0$ is a virtual origin, follows immediately from the variation of the mean velocity, the constancy of the local turbulent intensity and the ratio between the axial and transverse velocity variance. Second, the limit at small separations of the two-point budget equation yields an exact relation illustrating the equilibrium between the skewness of the longitudinal velocity derivative
$x_0$ is a virtual origin, follows immediately from the variation of the mean velocity, the constancy of the local turbulent intensity and the ratio between the axial and transverse velocity variance. Second, the limit at small separations of the two-point budget equation yields an exact relation illustrating the equilibrium between the skewness of the longitudinal velocity derivative 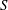 $S$ and the destruction coefficient
$S$ and the destruction coefficient 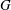 $G$ of enstrophy. By comparing the latter relation with that for homogeneous isotropic decaying turbulence, it is shown that the approach towards the asymptotic state at infinite Reynolds number of
$G$ of enstrophy. By comparing the latter relation with that for homogeneous isotropic decaying turbulence, it is shown that the approach towards the asymptotic state at infinite Reynolds number of 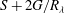 $S+2G/R_{\lambda }$ in the jet differs from that in purely decaying turbulence, although
$S+2G/R_{\lambda }$ in the jet differs from that in purely decaying turbulence, although 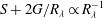 $S+2G/R_{\lambda } \propto R_{\lambda }^{-1}$ in each case. This suggests that, at finite Reynolds numbers, the transport equation for
$S+2G/R_{\lambda } \propto R_{\lambda }^{-1}$ in each case. This suggests that, at finite Reynolds numbers, the transport equation for  $\overline{\epsilon }$ imposes a fundamental constraint on the balance between
$\overline{\epsilon }$ imposes a fundamental constraint on the balance between 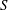 $S$ and
$S$ and 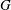 $G$ that depends on the type of large-scale forcing and may thus differ from flow to flow. This questions the conjecture that
$G$ that depends on the type of large-scale forcing and may thus differ from flow to flow. This questions the conjecture that 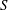 $S$ and
$S$ and 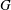 $G$ follow a universal evolution with
$G$ follow a universal evolution with 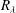 $R_{\lambda }$; instead,
$R_{\lambda }$; instead, 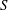 $S$ and
$S$ and 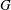 $G$ must be tested separately in each flow. The implication for the constant
$G$ must be tested separately in each flow. The implication for the constant 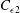 $C_{\epsilon 2}$ in the
$C_{\epsilon 2}$ in the 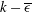 $k-\overline{\epsilon }$ model is also discussed.
$k-\overline{\epsilon }$ model is also discussed.