2.1. Numerical simulations

The simulations are performed using SBLI, an in-house, scalable, high-order, multi-block, compressible flow solver with shock-capturing capabilities (Yao et al. Reference Yao, Shang, Castagna, Johnstone, Jones, Redford, Sandberg, Sandham, Suponitsky and De Tullio2009). This solver has been extensively used to study transonic buffet (Zauner, De Tullio & Sandham Reference Zauner, De Tullio and Sandham2019; Zauner & Sandham Reference Zauner and Sandham2020; Moise et al. Reference Moise, Zauner and Sandham2022a,Reference Moise, Zauner, Sandham, Timme and Heb; Zauner et al. Reference Zauner, Moise and Sandham2023) and LFO (Almutairi et al. Reference Almutairi, Jones and Sandham2010; Almutairi & AlQadi Reference Almutairi and AlQadi2013) for various flow conditions. Fourth-order and third-order finite-difference schemes are used for spatial and temporal discretisation, respectively. The spectral-error-based implicit approach is used for LES (Jacobs et al. Reference Jacobs, Zauner, De Tullio, Jammy, Lusher and Sandham2018; Zauner & Sandham Reference Zauner and Sandham2020), which involves the application of a weak, low-pass, sixth-order spatial filter when required.

The configuration considered is that of an unconfined flow undergoing free transition over a NACA0012 infinite-wing section with a blunt trailing edge of thickness $0.5\,\%$ chord (results for a few cases of Dassault Aviation's V2C profile are also reported in Appendix A). The profile is extruded in the spanwise direction for a width of $L_z$, where $z$ denotes the spanwise direction. The streamwise and third orthonormal Cartesian directions are denoted as $x$ and $y$, respectively. For non-zero incidence angles, the chord-based coordinate directions are denoted by $x'$ and $y'$, respectively. The aerofoil is treated as an isothermal wall, whereas periodic boundary conditions are applied in the spanwise direction. Non-reflecting integral characteristic boundary conditions are used on the inflow boundaries, while zonal characteristic boundary conditions (Sandberg & Sandham Reference Sandberg and Sandham2006) are applied on the outflow boundaries. These boundaries are located sufficiently far from the aerofoil to not affect the near-field characteristics, with the inflow and outflow boundaries at an approximate distance of 7.5 and 4.5 chord lengths from the leading edge, respectively, (i.e. the same distances as used in Moise et al. Reference Moise, Zauner and Sandham2022a). Shock waves in the flow field are captured using a total-variation diminishing scheme.

2.2. Simulation parameters and grid features

The length, velocity, density and temperature scales used to solve the Navier–Stokes equations in dimensionless form are the aerofoil chord and corresponding free-stream values. The flow parameters, free-stream Mach number, $M$, and Reynolds number, $Re$, are calculated based on these scales. These parameters and the incidence angle, $\alpha$, are the main set of parameters varied in this study. We begin in § 3.1 by varying only $M$ and examine type I buffet for the NACA0012 aerofoil at $Re = 5\times 10^4$ and $\alpha = 0^\circ$. The effect of varying only the spanwise width is briefly considered in § 3.2 for the $M = 0.75$ case from § 3.1 (and $M = 0.8$ case in Appendix B). Following this, in § 4.1 we increase $\alpha$ whilst reducing $M$ (to stay within the buffet boundaries) at $Re = 5\times 10^4$ to link type I buffet with LFO. Next, in § 4.2 we examine the link with type II buffet by performing simulations at higher $Re$ while varying $M$ and $\alpha$ as required, so as to stay within buffet boundaries. Additionally, simulation results for Dassault Aviation's supercritical V2C aerofoil at zero incidence and $Re = 5\times 10^4$ are reported in Appendix A. To further generalize the conclusions, results from other previous studies on transonic buffet involving different aerofoils and transition conditions are also reproduced and discussed in § 5.1. The parameters studied in each of the following sections are outlined in table 1 and also provided along with a summary of buffet features at the start of each section.

Table 1. Flow parameters and conditions for all simulations discussed in various sections of this paper. The results discussed in § 5.1 for aerofoils other than the NACA0012 are based on other studies.

The fluid is assumed to be a perfect gas with a specific heat ratio of $\gamma = 1.4$ and satisfying Fourier's law of heat conduction. The Prandtl number is 0.72. It is also assumed to be Newtonian and satisfying Sutherland's law for viscosity, with the Sutherland constant as 110.4 K for a reference temperature of 268.67 K. The time step used is $3.2\times 10^{-5}$ (implying approximately $5\times 10^5$ iterations in a buffet cycle). For the lowest free-stream Mach number considered, $M = 0.3$, the time step is lowered to $1.6\times 10^{-5}$ that was found to be required to capture the relative increase in the speed of acoustic waves.

Multi-block C-H grids are used for the simulations. The grid points are first generated in the $x$–$y$ plane, following which the domain is extruded in the spanwise direction by generating points in that direction with a constant grid spacing. Given the large variations in $\alpha$ considered, two different grids are used. Grid 0 (figure 1a) is used for zero and low incidence angles ($\alpha \leq 4^\circ$) and contains a symmetric distribution of grid points on the suction and pressure side. By contrast, grid 1 (figure 1b), which is used for higher $\alpha$ (at which flow dynamics vary strongly on the suction side), has a lower resolution on the pressure side. These grids were generated using an open-source code (Zauner & Sandham Reference Zauner and Sandham2018). Since this code generates the grid-point positions in the $x$–$y$ plane based on spacing requirements, curvature, etc., it can be easily adapted to generate grids with similar characteristics for different aerofoils. Here, for grid 1, we use a similar distribution in the $x$–$y$ plane as that used for LES of flow over Dassault Aviation's V2C aerofoil and ONERA's OALT25 in previous studies (Zauner & Sandham Reference Zauner and Sandham2020; Moise et al. Reference Moise, Zauner and Sandham2022a; Zauner et al. Reference Zauner, Moise and Sandham2023). The three-dimensional grids based on grid 0 and grid 1 contain approximately 82 and 75 million points, respectively. The wall-normal grid spacing at the aerofoil surface varies between $\Delta \eta _w = 1\times 10^{-4}$ and $2\times 10^{-4}$, whilst the wall-parallel spacing between adjacent points on the aerofoil varies in the range $\Delta \xi _w = 3\times 10^{-4}$ and $4\times 10^{-3}$. For the majority of the cases considered, since $Re = 5\times 10^4$, the boundary layer remains laminar over most of the aerofoil surface and transition occurs only in the wake. For the few higher $Re$ cases considered, a turbulent boundary layer is observed in the vicinity of the shock foot. In these regions, the wall-parallel and wall-normal grid spacings at the wall, scaled based on wall units, satisfy $\Delta \xi _w^+ \approx 10$ and $\Delta \eta _w^+ \approx 1$.

Figure 1. Features of (a) grid 0 and (b) grid 1 in the vicinity of the NACA0012 aerofoil in the $x$–$y$ plane (only every 10th point shown for clarity).

Note that the LES result at $Re = 5\times 10^5$ using V2C's equivalent grid to grid 1 has been shown to match well with a direct numerical simulation employing a refined grid (Zauner & Sandham Reference Zauner and Sandham2020). Additionally, the grid for OALT25 that is equivalent to grid 1 has also been shown to capture buffet frequency accurately for $Re = 3\times 10^6$ (see the comparison with LES of Dandois et al. (Reference Dandois, Mary and Brion2018) and experiments of Brion et al. (Reference Brion, Dandois, Mayer, Reijasse, Lutz and Jacquin2020) reported in Zauner et al. Reference Zauner, Moise and Sandham2023). Thus, the present choices of grid distributions in the $x$–$y$ plane associated with grid 1 and grid 0 (which is even further resolved) are considered more than adequate to capture features at a relatively lower Reynolds number of $Re = 5\times 10^4$. The spanwise resolution is chosen as $\Delta z = 0.002$ for cases where $Re = 5\times 10^4$ and $\Delta z = 0.001$ for $Re \geq 5\times 10^5$ (turbulent boundary layer, $\Delta z^+_w \approx 10$), the latter being the same as that used in the LES of Zauner & Sandham (Reference Zauner and Sandham2020). The domain dimensions chosen here have been shown to be adequate previously in Moise et al. (Reference Moise, Zauner and Sandham2022a). In that study it was reported that extending the boundaries by a further 40 % (i.e. 10.5 chords) does not have any significant effect on flow features (difference in mean and root-mean-square values of the lift coefficient and difference of buffet frequency for the two cases is less than $10^{-2}$).

2.3. Spectral proper orthogonal decomposition

Spectral orthogonal decomposition is employed in the present study to examine spatio-temporally coherent features in the LES flow field (Lumley Reference Lumley1970; Glauser, Leib & George Reference Glauser, Leib and George1987; Towne, Schmidt & Colonius Reference Towne, Schmidt and Colonius2018). The methodology adopted is the same as that extensively discussed in Moise et al. (Reference Moise, Zauner and Sandham2022a) and only a brief summary is given here. For a zero-mean, stationary, stochastic process, the ideal basis that represents a given ensemble of its realisations consists of the eigenfunctions, $\boldsymbol {\psi }$, of the cross-spectral density tensor, $\boldsymbol{\mathsf{S}}$, satisfying

(2.1)\begin{equation} \int_\varOmega \boldsymbol{\mathsf{S}}(\boldsymbol{x},\boldsymbol{x'},St)\boldsymbol{\mathsf{W}}\boldsymbol{\psi}(\boldsymbol{x},St)\,{\rm d}\varOmega = \lambda(St) \boldsymbol{\psi}(\boldsymbol{x'},St). \end{equation}

Here, $\boldsymbol{\mathsf{W}}$ is a weight associated with the appropriate inner product on the spatial domain, $\varOmega$, $\boldsymbol {x}$ and $\boldsymbol {x'}$ are any two points in the domain, $St$ is the Strouhal number based on aerofoil chord and free-stream velocity, and $\lambda$ represents the eigenvalue. The eigenvalues are indexed in decreasing order (i.e. $\lambda _1 > \lambda _2 > \cdots \lambda _i > \cdots$), where $\lambda _i$ is referred to as the $i$th eigenvalue. The corresponding eigenfunctions are also indexed accordingly, implying that the expected value of the projection of $\boldsymbol {\psi }_1$ with the realisations is the maximum. Note that $\boldsymbol {\psi }_i(\boldsymbol {x},St_0)$ gives the spatial structure of the $i$th SPOD mode at a specific Strouhal number, $St_0$. The temporal behaviour of this SPOD mode is given by

(2.2)\begin{equation} \boldsymbol{\phi}_i(\boldsymbol{x},t) = \mathrm{Re}\{\boldsymbol{\psi}_i(\boldsymbol{x},St_0) \exp(2{\rm i}{\rm \pi} St_0 t)\}\!, \end{equation}

where $t$ represents time and $\mathrm {Re}\{\}$ denotes the real part. This can be rewritten as

(2.3)\begin{equation} \boldsymbol{\phi}_i(\boldsymbol{x},\phi) = \mathrm{Re}\{\boldsymbol{\psi}_i(\boldsymbol{x},St_0) \exp({\rm i}\phi) \}\!, \end{equation}

where $\phi = 2{\rm \pi} St_0 t$ is the phase within an oscillation cycle of frequency, $St_0$.

In this study we use the streaming algorithm and the numerical code provided in Schmidt & Towne (Reference Schmidt and Towne2019) to perform SPOD. Flow-field data based on the $z=0$ plane are stored at intervals of 0.16 (i.e. sampling frequency of 6.25). Each snapshot consists of the density, pressure and velocity fields. These snapshots are grouped into blocks such that at least three buffet cycles are captured in the time interval, $T_B$, associated with each block (for example, when buffet frequency, $St_b \approx 0.025$, $T_B = 120$, implying 750 snapshots per block). To compute $\boldsymbol {S}$, Welch's approach was employed with a Hamming window function and 50 % overlap of snapshots between blocks. The approximated cell area associated with each grid point was used to compute the weight matrix, $\boldsymbol {W}$. The SPOD algorithm used reduces the computational expense by computing only a subset of the eigenvalues and corresponding SPOD modes. Here, only the first two dominant eigenvalues (indices 1 and 2) were computed. No significant changes in the dominant eigenvalue and eigenfunction occurred when the parameters governing SPOD (block size, sampling frequency, etc.) were changed, indicating the robustness of the approach. Additionally, in our previous study (Moise et al. Reference Moise, Zauner, Sandham, Timme and He2022b), we matched the SPOD modes from LES with modes from global linear stability analysis based on RANS results for transonic buffet on the V2C aerofoil at similar flow conditions as the present study.

3.1. Effect of free-stream Mach number

The temporal variation of the lift coefficient past transients is shown for different free-stream Mach numbers, $M$, in figure 2(a). Periodic oscillations at a low frequency (time period, $T \sim O(10)$) are evident for all cases except $M = 0.6$ and 0.9. These oscillations will be shown to be related to transonic buffet. The variation of the lift coefficient within a shorter time interval is provided in figure 2(b), indicating oscillations at a higher frequency ($T \sim O(1)$) for all $M$. These will be shown to be related to the wake mode reported in other studies (Moise et al. Reference Moise, Zauner and Sandham2022a,Reference Moise, Zauner, Sandham, Timme and Heb). The power spectral densities of the fluctuating component of the lift coefficient for different $M$ are provided in figure 3(a). The peaks associated with these low- and high-frequency oscillations are highlighted using circles and diamonds, respectively. The amplitudes and frequency associated with these peaks are also documented in table 2. The energy associated with the latter is found to be approximately the same except for the case of $M = 0.9$. By contrast, the energy is negligible for the former at $M = 0.6$ and $M=0.9$, indicating buffet onset and offset, respectively. Buffet frequency is seen to increase monotonically with $M$, a trend which matches that reported in other studies on type II transonic buffet (Dor et al. Reference Dor, Mignosi, Seraudie and Benoit1989; Jacquin et al. Reference Jacquin, Molton, Deck, Maury and Soulevant2009; Brion et al. Reference Brion, Dandois, Mayer, Reijasse, Lutz and Jacquin2020; Moise et al. Reference Moise, Zauner and Sandham2022a). A scalogram based on the fluctuating component of the lift coefficient is plotted in figure 3(b) for a representative case of $M = 0.75$. This was computed using a continuous wavelet transform based on a Morse wavelet (symmetry parameter and time-bandwidth product chosen as 3 and 60, respectively) and a dimensionless sampling frequency of 62.5. The temporal variation of the lift coefficient is overlaid on the plot for reference (black curve). It can be inferred from the figure that there are temporal variations in the intensity of the high-frequency oscillations within a period of the low-frequency cycle, indicating that the wake mode behaviour is modulated by buffet oscillations, similar to the results reported in Moise et al. (Reference Moise, Zauner and Sandham2022a) for a different aerofoil and flow conditions.

Figure 2. Temporal variation of lift coefficient past transients for NACA0012 aerofoil at $Re = 5\times 10^4$, zero incidence and different free-stream Mach numbers (a) till the end of simulation indicating oscillations at a low frequency associated with buffet and (b) for a shorter time interval (interval shown using dashed lines in a), highlighting oscillations at a higher frequency associated with a von Kármán vortex street.

Figure 3. (a) Power spectral density (PSD) of the fluctuating component of lift coefficient as a function of the Strouhal number, $St$ for $\alpha = 0^\circ$ and different $M$ for the NACA0012 aerofoil at $Re = 5\times 10^4$ and $\alpha = 0^\circ$. Circles and diamonds highlight the peaks at Strouhal numbers associated with buffet and wake modes, respectively. (b) Scalogram for $M = 0.75$ based on the fluctuating lift coefficient. For reference, $C_L'(t)+2$ is overlaid on the scalogram as a black curve.

Table 2. Comparison of buffet and wake mode features for $L_z = 0.05$, $\alpha = 0^\circ$, $Re = 5\times 10^4$ and different $M$ for the NACA0012 aerofoil (all cases reported in § 3.1).

Henceforth, we focus on the three cases of $M = 0.8$, $0.75$ and 0.72. The instantaneous spatial flow field at approximately the high- and low-lift phases of the low-frequency cycle for these cases are shown in figure 4 using contours of the streamwise density gradient. Note that this field is similar to Schlieren visualisations in experiments. The sonic line (white curve), i.e. the isoline based on the instantaneous local Mach number, $M_{loc} = 1$, is overlaid for reference and delineates the supersonic region in the flow. For all three cases, the boundary layer separates at $x \approx 0.4$ (e.g. see figure 10b), with the separation point moving periodically upstream and downstream. Due to the use of a symmetric aerofoil, the flow field in the low-lift phase approximately mirrors (about the $x'$ axis) that in the high-lift phase (i.e. pressure-side features observed on the suction side and vice versa). The case, $M = 0.8$, is shown in figure 4(a,d), where there are supersonic regions on both sides of the aerofoil that are terminated by shock waves. In the high-lift phase the supersonic region on the suction side is significantly larger with multiple shock waves, whereas these features are inverted in the low-lift phase. This implies that the shock waves traverse the range $0.3 \leq x \leq 0.7$ on both sides. This is also seen in the temporal variation of these contours visualised in supplementary movie 1 available at https://doi.org/10.1017/jfm.2023.1065. Thus, this case of $M = 0.8$ can be categorised as a type I laminar transonic buffet. We emphasise that, whereas the presence of a single shock wave is typical for transonic buffet under forced-transition conditions or sufficiently high $Re$, laminar transonic buffet at lower $Re$ can have multiple shock waves present (Zauner et al. Reference Zauner, De Tullio and Sandham2019). Irrespective of the number of shock waves or transition type, transonic-buffet features have been shown to be similar (difference in $St$ between cases is approximately $10^{-2}$ and the SPOD modes’ spatial structures have strong visual resemblance) (Moise et al. Reference Moise, Zauner, Sandham, Timme and He2022b; Zauner et al. Reference Zauner, Moise and Sandham2023).

Figure 4. Streamwise density gradient contours on the $x$–$y$ plane shown at the approximate (a–c) high- and (d–f) low-lift phases of the low-frequency cycle for the NACA0012 aerofoil at $Re = 5\times 10^4$, $\alpha = 0^\circ$ and (a,d) $M = 0.8$, (b,e) $M = 0.75$ and (c,f) $M = 0.72$. The sonic line is highlighted using a white curve.

For a lower free-stream Mach number of $M = 0.75$ (figure 4b,e), the supersonic region is observed in the high-lift phase only on the suction side and is drastically reduced in area. Indeed, there are large time intervals within the low-frequency cycle in which the flow remains subsonic, as seen from supplementary movie 2. Furthermore, in the high- and low-lift phases, the transition from supersonic to subsonic flow is gradual, suggesting the absence of shock waves in the flow field. Nevertheless, the power spectral density (PSD) of the low-frequency peak in figure 3(a) does not significantly change, implying strong flow oscillations. At an even lower $M = 0.72$ (figure 4c,f) the flow was observed to be subsonic at all times (see movie 3), with the maximum instantaneous local Mach number being $\max (M_{local}) \leq 0.95$. From these results, it can be inferred that oscillations resembling transonic buffet occur even in the absence of shock waves for these flow conditions. This is further corroborated by examining the critical pressure coefficient, defined as the pressure coefficient at which the sonic conditions are expected to be reached for an isentropic flow over a body. It is given by

(3.1)\begin{equation} C_{p,{crit}} = \frac{2}{\gamma M^2}\left[\left(\frac{2+(\gamma-1)M^2}{\gamma+1}\right)^{{\gamma}/({\gamma-1})} -1\right]\!. \end{equation}

For the present case of $M = 0.72$, $C_{p,{crit}} \approx -0.7$. This is compared with the minimum value of the instantaneous pressure coefficient computed over the aerofoil surface at each time instant; see figure 5(a) ($y$ axis reversed). It is evident that the minimum value attained at each instant is higher than the critical value, suggesting that sonic conditions are never attained in the flow. The chordwise variation of the instantaneous pressure coefficient at high- and low-lift phases, $C_{p, {high}}$ and $C_{p, {low}}$, which occur at times $t_{high}$ and $t_{low}$ (highlighted as vertical lines in figure 5a) and the mean pressure coefficient, $\bar {C}_p$, are compared with $C_{p, {crit}}$ in figure 5(b). As expected, they are higher than $C_{p,{crit}}$ at all $x$. These figures indicate that both shock waves and supersonic regions are not essential for the sustenance of these oscillations.

Figure 5. (a) Temporal variation of the minimum instantaneous pressure coefficient on the aerofoil surface compared with $C_{p, {crit}}$. (b) Comparison of instantaneous and mean $C_p$ on the aerofoil upper surface with $C_{p, {crit}}$. The results shown are for the NACA0012 aerofoil at $Re = 5\times 10^4$, $\alpha = 0^\circ$ and $M = 0.72$.

The frequency variation of the first two eigenvalues obtained using a SPOD is shown in figure 6(a) for the representative case of $M = 0.75$. At the buffet frequency, it is seen that the energy content associated with the second SPOD mode is an order of magnitude smaller compared with the first, while there is significant energy content in the second SPOD mode at higher frequencies ($St \approx 3$). Since the focus of this study is on buffet, only the dominant eigenvalue and its eigenfunction from SPOD (i.e. $\lambda _1$ and $\boldsymbol {\psi }_1$) are further considered. The spectra associated with the dominant eigenvalue for various $M$ are compared in figure 6(b). Similarities with the spectra based on the lift coefficient (figure 3a) are evident, and we refer to the SPOD modes associated with the low- and high-frequency peaks as buffet and wake modes, respectively. The spatial structure of these modes is compared for different $M$ in figure 7 using contours of pressure. Note that to facilitate comparisons, a reference phase in the oscillation cycle of a SPOD mode from (2.3) needs to be chosen. In this study, unless otherwise mentioned, the reference phase is chosen as the phase relative to the instant when the lift fluctuation (computed using the SPOD mode's pressure field) reaches a maximum in an oscillation cycle. Additionally, the entire temporal variation within a buffet cycle is provided for the cases of $M = 0.75$ and 0.8 (supplementary movies 4 and 5).

Figure 6. (a) Eigenvalue spectra (logarithmic scale) from SPOD shown for (a) the first (dominant) and second eigenvalue for the case $M = 0.75$, and (b) only the dominant eigenvalue for different $M$ for the NACA0012 aerofoil at $Re = 5\times 10^4$ and $\alpha = 0^\circ$. Circles and diamonds highlight the peaks associated with the buffet and wake modes, respectively.

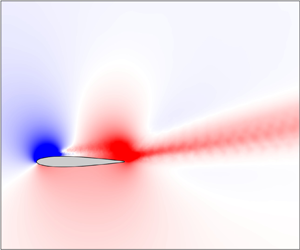
Figure 7. Buffet (a–c) and wake (d–f) modes from SPOD are shown using contour plots of the pressure field for the NACA0012 aerofoil at $Re = 5\times 10^4$, $\alpha = 0^\circ$ and (a,d) $M = 0.8$, (b,e) $M = 0.75$ and (c,f) $M = 0.72$.

The pressure fields of the wake modes for all $M$ resemble a von Kármán vortex street pattern. Additionally, pressure waves that originate from near the trailing edge can be observed. The buffet modes for all $M$ also resemble each other. Note that for a type I buffet, the same features seen on the suction side are mirrored on the pressure side, but of opposite sign. Focusing on the suction side, it is seen that the pressure reduction above the aerofoil (large blue region) is coupled with a pressure increase in a small region in the wake (narrow red stripe). This spatial structure is an essential characteristic of transonic buffet as discussed later in § 5.1. Thus, in addition to the similarity in frequency, it is seen that the spatial structure of the coherent oscillations is qualitatively similar under visual inspection (a quantitative description of this similarity is provided in § 5.2) irrespective of whether the flow is transonic or not, corroborating previous conclusions. We also note that while the symmetric NACA0012 aerofoil is the focus of this study (motivated by results reported in Bouhadji & Braza Reference Bouhadji and Braza2003; Jones et al. Reference Jones, Sandberg and Sandham2006), oscillations resembling transonic buffet can also occur for supercritical aerofoils, as shown in Appendix A for Dassault Aviation's V2C aerofoil at $\alpha =0^\circ$. This is seen for the V2C aerofoil for parametric values almost the same as NACA0012 aerofoil and the SPOD modes also have a similar spatial structure.

In summary, self-sustained oscillations at a low frequency of $St \approx 0.06$ can be observed for the NACA0012 aerofoil at zero incidence for a free-stream Reynolds number of $Re = 50\,000$. These resemble type I transonic buffet, but appear irrespective of whether the flow is transonic or not. Thus, it is established in this section that shock waves are not essential for type I transonic buffet to occur. In conjunction with the result that transonic buffet offset occurs at $M = 0.9$, this implies that shock waves are neither necessary nor sufficient for these oscillations to sustain. Henceforth, we will use ‘transonic buffet’ and ‘transonic-buffet-like oscillations’ (TBLO) to distinguish between cases for which the flow remains always transonic and for which it does not, respectively, and ‘buffet’ to collectively refer to either.

3.2. Effect of spanwise extent

Although transonic buffet on unswept infinite-wing sections is essentially two- dimensional, it has been shown in Zauner & Sandham (Reference Zauner and Sandham2020) that the spanwise width can have a significant effect on its amplitude (but not frequency). Motivated by this, we examined the amplitudes of the TBLO that occur at $M = 0.75$ for wider spanwise widths of $L_z = 0.1$, 0.25, 0.5 and 1. A similar study for transonic buffet at $M = 0.8$ is presented in Appendix B. The temporal variation of the lift coefficient and its PSD are shown in figure 8. The Strouhal number and the power spectral densities of the peaks in the spectra (buffet and wake modes denoted by subscripts ‘$b$’ and ‘$w$’) are also documented in table 3. The effect of $L_z$ on both $St_b$ and $St_w$ is negligible. However, the spanwise width has a strong effect on the amplitude of the oscillations, with the sharpest drop observed when $L_z$ is doubled from 0.05 to 0.1. A further increase in $L_z$ leads to smaller reductions in the amplitude, although sinusoidal oscillations are evident for all cases examined, including $L_z = 1$ (grey curve). Note that for all cases, there are variations in the amplitudes between buffet cycles (i.e. irregular cycles), although the oscillations are persistent.

Figure 8. (a) Temporal variation of lift coefficient past transients and (b) PSD of its fluctuating component as a function of the Strouhal number for the NACA0012 aerofoil at $Re = 5\times 10^4$, $\alpha = 0^\circ$ and $M = 0.75$ for different spanwise domain widths. Circles and diamonds highlight the buffet and wake mode Strouhal numbers, respectively.

Table 3. Comparison of buffet and wake mode features for $M = 0.75$, $\alpha = 0^\circ$, $Re = 5\times 10^4$ and different spanwise widths for the NACA0012 aerofoil (all cases reported in § 3.2).

Examining the spatio-temporal flow field in the $x$–$y$ plane, it was found that TBLO features are qualitatively similar for all $L_z$ (see supplementary movie 6 for the case $L_z = 1$). The SPOD spectra were also found to be similar, with peaks present at buffet and wake mode frequencies (not shown for brevity). The spatial features of these modes are shown for a few select cases in figure 9 and can be seen to be qualitatively similar. Overall, the only major difference observed was that, unlike the case of $L_z = 0.05$, where the flow has a small supersonic region in the high- and low-lift phases (see white curve highlighting sonic line in figure 4b,e), the flow remains subsonic at all times for wider domains (see movie 6). Thus, the conclusion that TBLO can be sustained in the subsonic regime holds true even for the largest span considered. Nevertheless, these results suggest that the spanwise extent somehow plays a crucial role in determining buffet amplitude. This is further confirmed by examining the mean flow features. The time- and span-averaged pressure and skin-friction coefficients are compared for different $L_z$ in figure 10. It can be inferred from these plots that the mean flow is not significantly altered by the variation in spanwise width, even for the cases of $L_z = 0.05$ and $L_z = 0.1$ for which the PSD changes by a factor of approximately four. Assuming that buffet arises as a global instability (Crouch et al. Reference Crouch, Garbaruk and Magidov2007), this implies that the growth and/or saturation features of this instability are strongly affected by the spanwise width. This trend is also observed in the presence of shock waves (i.e. type I transonic buffet), as shown in Appendix B. However, these results cannot be generalized – for type II transonic buffet on the supercritical V2C aerofoil, Zauner & Sandham (Reference Zauner and Sandham2020) showed that amplitudes of oscillations increase with an increase in span, which is opposite to the trend observed here.

Figure 9. Buffet (a–c) and wake (d–f) modes from SPOD are shown using contour plots of the pressure field for the NACA0012 aerofoil at $Re = 5\times 10^4$, $\alpha = 0^\circ$ and $M = 0.75$ for (a,d) $L_z = 0.1$, (b,e) $L_z = 0.5$ and (c,f) $L_z = 1$.

Figure 10. Time- and span-averaged (a) pressure coefficient and (b) skin-friction coefficient variation along the aerofoil surface for the NACA0012 aerofoil, $Re = 5\times 10^4$ and $\alpha = 0^\circ$, $M = 0.75$ and different domain widths. Here $\bar {C}_f = 0$ is highlighted using a dashed line in (b).

Although the imposition of periodic boundary conditions in the spanwise direction can artificially confine the flow, nevertheless, it provides a controlled numerical experiment that highlights the crucial role that three-dimensional features can play in determining buffet amplitude. This effect could arise from span-varying disturbances affecting boundary layer or wake transition characteristics, but the connection is not obvious. Further analysis towards understanding this effect is required, but we have restricted the scope of this study so as to focus on exploring the links between TBLO and transonic buffet.

4.1. Link between type I transonic buffet and LFO

The results at $\alpha = 0^\circ$ and $Re = 5\times 10^4$ discussed in the preceding section establish the link between type I transonic buffet and TBLO. To extend this further and relate with LFO that occur in the incompressible regime (i.e. low $M$) and close to stall (i.e. high $\alpha$), the $\alpha -M$ parameter space is further explored here by both increasing $\alpha$ and decreasing $M$ simultaneously at this $Re$ so as to remain in the narrow range where buffet occurs. It is emphasised that each simulation is performed with the same type of initial conditions of uniform flow and constant boundary conditions and incidence angle (i.e. this is not a hysteresis study). The incidence angles considered are $0^\circ$ to $8^\circ$ in steps of $2^\circ$, and additionally, $\alpha = 9.4^\circ$. For each $\alpha$, the free-stream Mach number required for the simulation was estimated based on the oscillation features observed at lower $\alpha$. Due to the numerical expense involved, no attempts were made to further vary $M$ at a given $\alpha$ as long as sustained oscillations were present at the estimated $M$. Also, based on the results reported in the previous section on domain extent, $L_z = 0.1$ was chosen for all the simulations in this section as a compromise between accuracy and numerical expense (see figure 8 and table 3). All cases reported in this section and their buffet characteristics are summarised in table 4.

Table 4. Comparison of buffet and wake mode features for $L_z = 0.1$, $Re = 5\times 10^4$ and different ($M,\alpha$) for the NACA0012 aerofoil (all cases considered in § 4.1; case, $\alpha = 0^\circ$, $M = 0.75$, included for reference).

The lift variations for a few of these cases are shown in figure 11(a,c,d). The variations are strongly irregular and this can make it difficult to discern if buffet occurs. Even for the case of $\alpha = 9.4$ and $M = 0.3$ (black curve) for which buffet can be visually inferred, there are periods when these oscillations at a low frequency are almost completely damped out, as seen, for example, in $100 \leq t-t_0 \leq 150$. However, these oscillations recover and remain persistent at later times of $t > 150$. The power spectral densities of lift fluctuations for all cases studied are shown in figure 11(b). A case at zero incidence ($M=0.75$, $L_z = 0.1$, discussed in § 3.2) is additionally provided for reference. It is evident that there are peaks in the spectra at a low frequency (highlighted by circles) indicating buffet for all cases, although there is variability in both $St_b$ and PSD$_b$. Unlike the monotonic increase in $St_b$ seen in § 3.1 when only $M$ is varied, the variation here does not have any specific trend. This is because although $M$ is increased, $\alpha$ is reduced simultaneously and transonic-buffet frequency can vary in a non-monotonic fashion when $\alpha$ is changed (cf. Moise et al. Reference Moise, Zauner and Sandham2022a, figure 17b). Similarly, note that the buffet amplitude at a given $\alpha$ has a nonlinear variation with $M$ (given that it is negligible at onset and offset values of $M$). Thus, monotonic trends in the frequency or amplitude of buffet are not expected when both $M$ and $\alpha$ are varied simultaneously. As shown later, SPOD confirms that the spatial structure of the modes associated with these peaks is consistent and that the modes are correlated (see figure 13 and § 5.2). Note that, unlike the zero incidence case, there is no discrete peak associated with a wake mode for the others. Instead, there is a broadband bump in the spectra centred about $St \approx 1$. A similar bump associated with wake modes is commonly reported for transonic buffet at non-zero incidences e.g. Moise et al. Reference Moise, Zauner and Sandham2022a). Shock waves were absent in the flow field for all non-zero incidence angles studied, implying that the sustained oscillations can be categorised as TBLO for these cases. For the cases considered in this section, when $\alpha \geq 4^\circ$, the energy content on the suction side was dominant and, thus, these cases will also be referred to as type II TBLO.

Figure 11. (a,c,d) Temporal variation of lift coefficient past transients for $M = 0.7$, $\alpha = 2^\circ$ (a), $M = 0.5$, $\alpha = 6^\circ$ (c) and $M = 0.3$, $\alpha = 9.4^\circ$ (d), and (b) PSD of its fluctuating component as a function of the Strouhal number, $St$ when $\alpha$ and $M$ varied simultaneously at $Re = 5\times 10^4$ for the NACA0012 aerofoil.

Contours of time- and span-averaged local Mach number, $\bar {M}_{loc}$, are shown for the cases of $\alpha = 8^\circ$, $M = 0.4$ and $\alpha = 9.4^\circ$, $M = 0.3$ in figure 12. The maximum $\bar {M}_{loc}$ attained is 0.65 for the former and 0.51 for the latter and most regions of the flow are found to have $\bar {M}_{loc} \leq 0.4$ for the latter case. Thus, it can be inferred that compressibility effects are insignificant in most of the flow field, especially when $\alpha = 9.4^\circ$ and $M = 0.3$. Although the requirement for a reduced time step prevented exploration at even lower $M$, the present trend of sustained oscillations occurring for decreasing maximum values, $\max (\bar {M}_{loc})$, with increasing $\alpha$ and decreasing $M$ suggests that these oscillations can also sustain in the incompressible regime. The peak in the spectrum for the lowest $M$ simulated occurs at a frequency similar to those reported in experiments studying LFO. For example, Rinoie & Takemura (Reference Rinoie and Takemura2004) reported $St_h = 0.008$, where $St_h$ is the Strouhal number based on the projected height ($h = c\sin \alpha$) and free-stream velocity. This result is for the NACA0012 profile at $Re = 1.3\times 10^5$ for $M \ll 0.3$ and is of the same order of magnitude as seen in the present study, with $St_h = St\times \sin \alpha \approx 0.005$ for $Re = 5\times 10^4$, $M = 0.3$ and $\alpha = 9.4^\circ$. Thus, we will also refer to the oscillations occurring at the lowest $M$ simulated in the present study as LFO.

Figure 12. Contours of $\bar {M}_{loc}$ for the NACA0012 aerofoil at $Re = 5\times 10^4$ and (a) $\alpha = 8^\circ$, $M = 0.4$ and (b) $\alpha = 9.4^\circ$, $M = 0.3$.

The SPOD modes associated with the low-frequency peaks are shown in figure 13 for the higher incidences simulated. Additionally, an animation showing the temporal variation of the SPOD mode is provided for the highest incidence simulated (supplementary movie 7). The spatial structure for all cases visually resembles that of type II transonic buffet. A closer look shows that they are also qualitatively similar to the type I buffet modes shown previously (cf. figure 7) when the suction side's features alone are considered. That is, for the present modes, a reduction of pressure on the fore part of the aerofoil (blue region) is coupled with an increase in pressure in the aft part, which extends into the wake (red region). The parametric variation indicates that the extent of the blue region spreads closer to the trailing edge as $\alpha$ is reduced. For the type I modes at zero incidence, the blue region extends to the trailing edge, but the wake region (red) is similar to that seen here. A quantitative comparison that shows the strong correlation between the buffet modes for different cases and the out-of-phase features of these zones is provided later in § 5.2.

Figure 13. Buffet modes from SPOD are shown using contour plots of the pressure field for the NACA0012 aerofoil at $Re = 5\times 10^4$ and (a) $\alpha = 6^\circ$, $M = 0.5$, (b) $\alpha = 8^\circ$, $M = 0.4$ and (c) $\alpha = 9.4^\circ$, $M = 0.3$.

In summary, these results demonstrate that both buffet frequency and spatio-temporal modal features (based on SPOD) are essentially the same for type I transonic buffet ($\alpha = 0^\circ$ and $M = 0.8$), TBLO (all cases considered in the current section) and LFO ($\alpha = 9.4^\circ$ and $M = 0.3$). Furthermore, the results directly link these phenomena by showing that TBLO can be sustained for intermediate values of $\alpha$ and $M$ by reducing $M$ appropriately when increasing $\alpha$. We again emphasise that these low-frequency TBLO are distinct from vortex shedding (i.e. wake modes). The latter accompanies TBLO for all the cases studied, but at a higher frequency (bump in spectra at $St \approx 1$) and is not the focus of this study.

4.2. Link between type II transonic buffet and LFO

Type II transonic buffet, with shock waves occurring and oscillating exclusively on the suction side, has been the focus of most recent studies, and in this section we try to establish links between this type and TBLO. Note that type II transonic buffet is not observed for any of the cases simulated at $Re = 5\times 10^4$. This is because offset conditions of type II TBLO and fully stalled conditions occur for $M$ below those at which shock waves appear. To link the type II TBLO observed at $\alpha = 4^\circ$ and $M = 0.7$ at this $Re$ with type II transonic buffet, a few more cases were simulated at higher $Re$. This is motivated by the observation in Zauner & Sandham (Reference Zauner and Sandham2018) that transonic buffet onset and offset can also occur with changes in $Re$. Grid requirements can vary significantly as $Re$ is increased and can lead to large computational expenses. Due to limited resources, it was not possible to explore the parametric space using small changes in values as done in previous sections and only two additional cases are considered here. Nonetheless, observed trends comply well with those seen in previous studies.

The parameters for the two additional cases simulated for which buffet occurs are $\alpha = 4^\circ$, $M = 0.75$ and $Re = 5\times 10^5$, and $\alpha = 6^\circ$, $M = 0.75$ and $Re = 1.5\times 10^6$ (see table 5). We will refer to these two as high-$Re$ cases. The parametric values associated with these cases were found by trial and error since type II transonic buffet occurs only in a narrow range of the parametric space. For these high-$Re$ cases, the grid used has the same distribution in the $x$–$y$ plane as grid 1. However, the spanwise grid spacing is halved to $\Delta z = 0.001$ to account for the increased $Re$. Considering the numerical expense, the narrower span of $L_z = 0.05$ is used. We emphasise that this configuration ($Re$, $L_z$ and $\Delta z$) is similar to that used in a majority of simulations carried out in our previous studies (Moise et al. Reference Moise, Zauner and Sandham2022a,Reference Moise, Zauner, Sandham, Timme and Heb; Zauner et al. Reference Zauner, Moise and Sandham2023), and for which various validations and verification have been performed with LES, DNS and experiments (see § 2).

Table 5. Comparison of buffet and wake mode features for the NACA0012 aerofoil (all cases considered in § 4.2; case, $\alpha = 4^\circ$, $M = 0.7$, $Re = 5\times 10^4$, $L_z = 0.05$, included for reference).

The variation of the lift coefficient and the PSD of its fluctuating component are shown in figure 14 for the three different $Re$ examined. In contrast to the irregular temporal variation of the lift coefficient observed at subsonic conditions ($Re = 5\times 10^4$), the high-$Re$ cases, for which the flow is transonic, exhibit a more regular temporal variation. The oscillation cycles for the latter are also dominated by the low-frequency content, as can also be inferred from the power spectra. A strong increase in the buffet frequency with $Re$ can be observed, from $St_b \approx 0.03$ at $Re = 5\times 10^4$ to $St_b \approx 0.12$ at $Re = 5\times 10^5$ and $St_b \approx 0.15$ at $Re = 1.5\times 10^6$. Note that it is not only $Re$ that is increased between cases, but also $M$ (or $\alpha$), and the latter can have a strong influence in increasing $St_b$ (e.g. figure 3a here and figure 8 in Zauner et al. Reference Zauner, Moise and Sandham2023).

Figure 14. (a,c,d) Temporal variation of lift coefficient past transients for the NACA0012 aerofoil at $Re$, $\alpha$ and $M$ of $5\times 10^4$, $4^\circ$ and $0.7$ (a), $5\times 10^5$, $4^\circ$ and $0.75$ (c), $1.5\times 10^6$, $6^\circ$ and $0.75$ (d). (b) Power spectral density of its fluctuating component as a function of the Strouhal number, $St$ when $Re$ is also varied.

The streamwise density gradient fields in the high- and low-lift phases are compared in figure 15. The presence of shock waves that exhibit a fore–aft motion on the suction surface can be inferred for the high-$Re$ cases. Thus, these two cases can be considered as examples of type II transonic buffet. We note that there are strong temporal variations in the boundary layer separation location between the high- and low-lift phases. This periodic fore–aft motion of the separation point is a characteristic feature of transonic buffet (see figure 18 in Moise et al. Reference Moise, Zauner, Sandham, Timme and He2022b) and further corroborates the conclusion that it is linked with LFO, which has been described as involving a quasi-periodic switching between stalled and unstalled conditions (Zaman et al. Reference Zaman, McKinzie and Rumsey1989).

Figure 15. Streamwise density gradient contours on the $x$–$y$ plane shown at the approximate (a–c) high- and (d–f) low-lift phases of the low-frequency cycle for the NACA0012 aerofoil at (a,d) $\alpha = 4^\circ$, $M = 0.7$, $Re = 5\times 10^4$; (b,e) $\alpha = 4^\circ$, $M = 0.75$, $Re = 5\times 10^5$ and (c,f) $\alpha = 6^\circ$, $M = 0.75$, $Re = 1.5\times 10^6$. The sonic line is highlighted using a white curve.

The buffet modes obtained from SPOD are compared in figure 16 for all cases. Comparing the cases of the lowest two $Re$ considered, the spatial structure of the modes appear similar under visual inspection, with a pattern of pressure reduction (blue) on the suction surface accompanying a pressure increase (red) near the trailing edge and the wake (see § 5.2 for quantitative comparisons). This pattern is qualitatively the same as that seen for LFO in figure 13, except that the region associated with the pressure reduction extends further downstream here. For the highest $Re$, the buffet mode is similar to the other cases except for the presence of a small region associated with a pressure increase on the suction side. However, the animation provided for the spatio-temporal mode (supplementary movie 8) shows that the spatial structures are closer at other time instants in the buffet cycle. This suggests that the choice of using the high-lift phase as the reference phase to compare modes from different cases is not always ideal, but sufficient to establish their similarities. This is confirmed by choosing a different reference phase and comparing the instantaneous features in figure 17. Here, the reference phase is chosen such that the pressure (from SPOD) on the upper corner of the blunt trailing edge is real-valued, which is similar to the approach adopted in Moise et al. (Reference Moise, Zauner, Sandham, Timme and He2022b).

Figure 16. Buffet modes from SPOD for the NACA0012 aerofoil are shown using contour plots of the pressure field for cases (a) $\alpha = 4^\circ$, $M = 0.7$, $Re = 5\times 10^4$; (b) $\alpha = 4^\circ$, $M = 0.75$, $Re = 5\times 10^5$ and (c) $\alpha = 6^\circ$, $M = 0.75$, $Re = 1.5\times 10^6$. The comparison is done by choosing the instant where the high-lift phase occurs as the reference phase.

Figure 17. Buffet modes from SPOD for the NACA0012 aerofoil are shown using contour plots of the pressure field for cases (a) $\alpha = 4^\circ$, $M = 0.7$, $Re = 5\times 10^4$; (b) $\alpha = 4^\circ$, $M = 0.75$, $Re = 5\times 10^5$ and (c) $\alpha = 6^\circ$, $M = 0.75$, $Re = 1.5\times 10^6$. The comparison is done by choosing the reference phase such that the pressure at the upper corner of the blunt trailing edge is real-valued.