Irregular conduits, complex surfaces, and porous media often manifest more than one geometric wetting condition for spontaneous capillary flows. As a result, different regions of the flow exhibit different rates of flow, all the while sharing common dynamical capillary pressure boundary conditions. 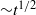The classic problem of sudden capillary rise in tubes with interior corners is revisited from this perspective and solved numerically in the self-similar visco-capillary limit à la Lucas–Washburn. Useful closed-form analytical solutions are obtained in asymptotic limits appropriate for many practical flows in conduits containing one or more interior corner. The critically wetted corners imbibe fluid away from the bulk capillary rise, shortening the viscous column length and slightly increasing the overall flow rate. The extent of the corner flow is small for many closed conduits, but becomes significant for flows along open channels and the method is extended to approximate hemiwicking flows across triangular grooved surfaces. It is shown that an accurate application of the method depends on an accurate a priori assessment of the competing viscous cross-section length scales, and the expedient Laplacian scaling method is applied herein toward this effect.