Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-27T07:31:33.441Z Has data issue: false hasContentIssue false
  • English
  • Français

Collision rate of ice crystals with water droplets in turbulent flows

Published online by Cambridge University Press:  27 April 2018

Aurore Naso Open the ORCID record for Aurore Naso [Opens in a new window] ,
Jennifer Jucha ,
Emmanuel Lévêque  and
Alain Pumir
Aurore Naso*
Affiliation:
Université de Lyon, Ecole Centrale de Lyon, Université Claude Bernard, CNRS, INSA de Lyon, Laboratoire de Mécanique des Fluides et d’Acoustique, 69134 Ecully, France
Jennifer Jucha
Affiliation:
Forschungszentrum Jülich, Projektträger Jülich, 52425 Jülich, Germany
Emmanuel Lévêque
Affiliation:
Université de Lyon, Ecole Centrale de Lyon, Université Claude Bernard, CNRS, INSA de Lyon, Laboratoire de Mécanique des Fluides et d’Acoustique, 69134 Ecully, France
Alain Pumir
Affiliation:
Université de Lyon, ENS de Lyon, Université Claude Bernard, CNRS, Laboratoire de Physique, 69342 Lyon, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Riming, the process whereby ice crystals get coated by impacting supercooled liquid droplets, is one of the dominant processes leading to precipitation in mixed-phase clouds. How a settling crystal collides with very small water droplets has been mostly studied in laminar conditions. The present numerical study aims at providing further insight on how turbulent flow motion affects the riming of ice crystals. We model the crystals as narrow oblate ellipsoids, smaller than the Kolmogorov elementary scale. By neglecting the effect of fluid inertia on the motion of the crystals and droplets, and using direct numerical simulations of the Navier–Stokes equations in a moderately turbulent regime, over a range of kinetic energy dissipation 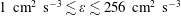$1~\text{cm}^{2}~\text{s}^{-3}\lesssim \unicode[STIX]{x1D700}\lesssim 256~\text{cm}^{2}~\text{s}^{-3}$ , we determine the collision rate between disk-shaped ice crystals and very small liquid water droplets. Whereas differential settling plays the dominant role in determining the collision rate at small turbulence intensity, the role of turbulence becomes more important at the large values of $\unicode[STIX]{x1D700}$ simulated, an effect that can be partly attributed to the increased role of inertia. We always find that collisions occur with a large probability on the rim of the ellipsoids, a phenomenon that can be explained to a large extent by kinematic considerations. The difference in the settling velocity of crystals and droplets induces a strong asymmetry in the probability of collision between the faces of the ellipsoids. Our results shed light on the physical mechanisms involved in the riming of ice crystals in clouds.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Turbulent Flows: Turbulent Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 845 , 25 June 2018 , pp. 615 - 641
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ayala, O., Rosa, B., Wang, L. P. & Grabowski, W. W. 2008 Effects of turbulence on the geometric collision rate of sedimenting droplets. Part 1. Results from direct numerical simulation. New J. Phys. 10, 075015.Google Scholar
von Blohn, N., Diehl, K., Mitra, S. K. & Borrmann, S. 2009 Riming of graupel: wind tunel investigations of collection kernels and growth regimes. J. Atmos. Sci. 66, 2359–2366.Google Scholar
von Blohn, N., Diehl, K., Mitra, S. K. & Borrmann, S. 2011 Wind tunnel experiments on the retention of trace gases during riming: nitric acid, hydrochloric acid and hydrogen peroxide. Atmos. Chem. Phys. 11, 11569–11579.Google Scholar
Bragg, A. D. & Collins, L. R. 2014a New insights from comparing statistical theories for inertial particles in turbulence: I. Spatial distributions of particles. New J. Phys. 16, 055013.Google Scholar
Bragg, A. D. & Collins, L. R. 2014b New insights from comparing statistical theories for inertial particles in turbulence: II. Relative velocities. New J. Phys. 16, 055014.Google Scholar
Butcher, J. C. 2004 Numerical Methods for Ordinary Differential Equations. John Wiley & Sons.Google Scholar
Candelier, F., Einarsson, J. & Mehlig, B. 2016 Angular dynamics of a small particle in turbulence. Phys. Rev. Lett. 117, 204501.Google Scholar
Chen, J. P. & Lamb, D. 1994 The theoretical basis for the paramterization of ice crystal habits: growth by vapor deposition. J. Atmos. Sci. 51, 1206–1221.Google Scholar
Choi, Y. K., Chang, J. W., Wang, W., Kim, M.-S. & Elber, G. 2009 Continuous collision for ellipsoids. IEEE Trans. Vis. Comput. Graphics 15, 311–325.Google Scholar
Chouippe, A. & Uhlmann, M. 2015 Forcing homogeneous turbulence in direct numerical simulation of particulate flow with interface resolution and gravity. Phys. Fluids 27 (12), 123301.Google Scholar
Chun, J. & Koch, D. L. 2005 Coagulation of monodisperse aerosol particles by isotropic turbulence. Phys. Fluids 17, 027102.CrossRefGoogle Scholar
Cox, R. G. 1965 The steady motion of a particle of arbitrary shape at small Reynolds numbers. J. Fluid Mech. 23, 625–643.Google Scholar
Diehl, K., Mitra, S. K., Szakall, M., von Blohn, N., Borrmann, S. & Pruppacher, H. R. 2011 The Mainz vertical wind tunnel facility – a review of 25 years of laboratory experiments on cloud physics and chemistry. In Wind Tunnels: Aerodynamics, Models and Experiments, pp. 69–92. Nova Science Publishers.Google Scholar
Elghobashi, S. & Truesdell, G. C. 1992 Direct simulation of particle dispersion in a decaying isotropic turbulence. J. Fluid Mech. 242, 655–700.Google Scholar
Falkovich, G. & Pumir, A. 2007 Sling effect in collisions of water droplets in turbulent clouds. J. Atmos. Sci. 64, 4497–4505.Google Scholar
Gatignol, R. 1983 The Faxén formulas for a rigid particle in an unsteady non-uniform Stokes-flow. J. Méc. Théor. Appl. 2 (2), 143–160.Google Scholar
Grabowski, W. & Vaillancourt, P. 1999 Comments on ‘Preferential concentration of cloud droplets by turbulence: effects on the early evolution of cumulus cloud droplet spectra’. J. Atmos. Sci. 56, 1433.Google Scholar
Grabowski, W. W. & Wang, L. P. 2013 Growth of cloud droplets in a turbulent environment. Annu. Rev. Fluid Mech. 45, 293.Google Scholar
Gustavsson, K., Jucha, J., Naso, A., Lévêque, E., Pumir, A. & Mehlig, B. 2017 Statistical model for the orientation of nonspherical particles settling in turbulence. Phys. Rev. Lett. 119, 254501.CrossRefGoogle ScholarPubMed
Gustavsson, K. & Mehlig, B. 2011 Distribution of relative velocities in turbulent aerosols. Phys. Rev. E 84, 045304.Google Scholar
Hall, W. D. 1980 A detailed microphysicl model within a two-dimensional dynamic framework: model description and preliminary results. J. Atmos. Sci. 37, 2486–2507.Google Scholar
Happel, J. & Brenner, H. 1983 Low Reynolds Number Hydrodynamics. Martinus Nijhoff.Google Scholar
Homann, H., Bec, J. & Grauer, R. 2013 Effect of turbulent fluctuations on the drag and lift forces on a towed sphere and its boundary layer. J. Fluid Mech. 721, 155–179.CrossRefGoogle Scholar
Huang, K. 1987 Statistical Mechanics. John Wiley & Sons.Google Scholar
Ireland, P. J., Bragg, A. D. & Collins, L. R. 2016 The effect of Reynolds number on inertial particle dynamics in isotropic turbulence. Part 2. Simulations with gravitational effects. J. Fluid Mech. 796, 659–711.Google Scholar
Jeffery, G. B. 1922 The motion of ellipsoid particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 102, 161–179.Google Scholar
Jucha, J., Naso, A., Lévêque, E. & Pumir, A. 2018 Settling and collision between small ice crystals in turbulent flows. Phys. Rev. Fluids 3, 014604.Google Scholar
Khayat, R. E. & Cox, R. G. 1989 Inertia effects on the motion of long slender bodies. J. Fluid Mech. 209, 435–462.Google Scholar
Kolmogorov, A. N. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds number. Dokl. Akad. Nauk SSSR 30, 301–305.Google Scholar
Leal, L. G. 1980 Particle motions in a viscous fluid. Annu. Rev. Fluid Mech. 12, 435–476.CrossRefGoogle Scholar
Lopez, D. & Guazzelli, E. 2017 Inertial effects on fibers settling in a vortical flow. Phys. Rev. Fluids 2, 024306.Google Scholar
Lucci, F., Ferrante, A. & Elghobashi, S. 2010 Modulation of isotropic turbulence by particles of Taylor length-scale size. J. Fluid Mech. 650, 5–55.Google Scholar
Maxey, M. R. & Riley, J. J. 1983 Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26 (4), 883–889.CrossRefGoogle Scholar
Naso, A. & Prosperetti, A. 2010 The interaction between a solid particle and a turbulent flow. New J. Phys. 12 (3), 033040.Google Scholar
Pruppacher, H. R. & Klett, J. D. 1997 Microphysics of Clouds and Precipitations. Kluwer.Google Scholar
Pumir, A. & Wilkinson, M. 2016 Collisional aggregation due to turbulence. Annu. Rev. Condens. Matter Phys. 7, 141–170.Google Scholar
Saffman, P. G. & Turner, J. S. 1956 On the collision of droplets in turbulent clouds. J. Fluid Mech. 1, 16–30.Google Scholar
Siewert, C., Kunnen, R. P. J., Meinke, M. & Schröder, W. 2014a On the collision detection for ellipsoidal particles in turbulence. In Proceedings of the ASME 2014 4th Joint US-European Fluids Engineering Division Summer Meeting. ASME paper FEDS2014-2198.Google Scholar
Siewert, C., Kunnen, R. P. J. & Schröder, W. 2014b Collision rates of small ellipsoids settling in turbulence. J. Fluid Mech. 758, 686–701.Google Scholar
Siewert, C., Kunnen, R. P. J. & Schröder, W. 2014c Orientation statistics and settling velocity of ellipsoids in decaying turbulence. Atmos. Res. 142, 45–56.Google Scholar
Sundaram, S. & Collins, L. R. 1996 Numerical considerations in simulating a turbulent suspension of finite-volume particles. J. Comput. Phys. 124 (2), 337–350.Google Scholar
Szakall, M., Kessler, S., Diehl, K., Mitra, S. K. & Borrmann, S. 2014 A wind tunnel study of the effects of collision processes on the shape and oscillation for moderate-size raindrops. Atmos. Res. 142, 67–78.Google Scholar
Vohl, O., Mitra, S. K., Wurzler, S. C. & Pruppacher, H. R. 1999 A wind tunnel study of the effects of turbulence on the growth of cloud drops by collision and coalescence. J. Atmos. Sci. 56, 4088–4099.Google Scholar
Voßkuhle, M., Lévèque, E., Wilkinson, M. & Pumir, A. 2013 Multiple collisions in turbulent flows. Phys. Rev. E 88, 063008.Google Scholar
Voßkuhle, M., Pumir, A., Lévêque, E. & Wilkinson, M. 2014 Prevalence of the sling effect for enhancing collision rates in turbulent suspensions. J. Fluid Mech. 749, 841–852.Google Scholar
Wang, L.-P., Ayala, O., Gao, H., Andersen, C. & Mathews, K. L. 2014 Study of forced turbulence and its modulation by finite-size solid particles using the lattice Boltzmann approach. Comput. Maths Applics 67, 363–380.Google Scholar
Wang, L. P., Ayala, O., Kasprzak, S. E. & Grabowski, W. W. 2005 Theoretical formulation of collision rate and collision efficiency of hydrodynamically interacting clould droplets in turbulent atmosphere. J. Atmos. Sci. 62, 2433–2450.Google Scholar
Wang, P. K. & Ji, W. 2000 Collision efficiencies of ice crystals at low-intermediate Reynolds numbers colliding with supercooled cloud droplets: a numerical study. J. Atmos. Sci. 57, 1001–1009.Google Scholar
Yang, P., Lou, K. N., Bin, L., Liu, C., Yi, B. & Baum, B. A. 2015 On the radiative properties of ice clouds: light scattering, remote sensing and radiation parametrization. Adv. Atmos. Sci. 32, 32–63.Google Scholar