2.1. Isolated bubble in an infinite medium

We begin by considering an isolated bubble in a Hele-Shaw cell of thickness $\hat {h}$ parallel to the $(\hat {x},\hat {y})$-plane. Under the lubrication approximation, in the limit where $\hat {h}$ is much smaller than the horizontal dimensions of the cell and the bubble, the flow away from the bubble is governed by the Hele-Shaw equations:

(2.1a)\begin{gather} \hat{\boldsymbol{v}} = \frac{3}{2}\,\hat{\boldsymbol{u}}\left(1-\frac{4\hat{z}^2}{\hat{h}^2}\right), \end{gather}

(2.1b)\begin{gather}\hat{\boldsymbol{\nabla}}\boldsymbol{\cdot}\hat{\boldsymbol{u}}= 0, \end{gather}

(2.1c)\begin{gather}\hat{\boldsymbol{u}} ={-}\frac{\hat{h}^2}{12\hat{\mu}}\,\hat{\boldsymbol{\nabla}} \hat{p}. \end{gather}

Here, $\hat {\boldsymbol {v}}(\hat {x},\hat {y},\hat {z})$ is the full fluid velocity profile, $\hat {\boldsymbol {u}}(\hat {x},\hat {y})$ is the depth-averaged fluid velocity, $\hat {z} \in [-\hat {h}/2,\hat {h}/2]$ denotes the height coordinate, $\hat {p}(\hat {x},\hat {y})$ is the leading-order pressure, and $\hat {\mu }$ is the fluid viscosity.

In this subsection, we focus on the simple model problem of a single bubble in a large cell with a prescribed uniform background flow of speed $\hat {U}$ in the $\hat {x}$-direction, which gives us the far-field condition

(2.2)\begin{equation} \hat{\boldsymbol{u}}\rightarrow \hat{U}\boldsymbol{i} \quad \text{as}\ \hat{x}^2 + \hat{y}^2 \rightarrow \infty, \end{equation}

where $\boldsymbol {i}$ is the unit vector in the $\hat {x}$-direction.

Looking down on the cell from above (figure 1a), the boundary of the bubble appears to be a closed curve in the $(\hat {x},\hat {y})$-plane, on which we impose the effective boundary conditions (Meiburg Reference Meiburg1989)

(2.3a)\begin{gather} \boldsymbol{n}\boldsymbol{\cdot} \hat{\boldsymbol{u}} = \hat{U}_n, \end{gather}

(2.3b)\begin{gather}\hat{p}_b - \hat{p} = \frac{2\hat{\gamma} }{\hat{h}} +\frac{2\hat{\gamma} }{\hat{h}}\,\beta({Ca}_{n})\,{Ca}_{n}^{2/3} + \frac{\hat{\gamma} {\rm \pi}}{4}\,\hat{\kappa}. \end{gather}

Here, $\boldsymbol {n}$, $\hat {U}_n$ and $\hat {\kappa }$ are the outward-pointing normal, normal velocity and curvature of the apparent bubble boundary, respectively; $\hat {\gamma }$ is the surface-tension parameter, $\hat {p}_b$ is the uniform pressure inside the bubble, ${Ca}_n = \hat {\mu } \hat {U}_n/\hat {\gamma }$ is the capillary number based on the normal velocity, and $\beta$ is the Bretherton coefficient, whose value depends on whether the meniscus is advancing or retreating (Bretherton Reference Bretherton1961; Wong, Radke & Morris Reference Wong, Radke and Morris1995; Halpern & Jensen Reference Halpern and Jensen2002):

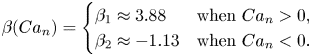(2.4)\begin{equation} \beta({Ca}_n)=\begin{cases} \beta_1 \approx 3.88 & \text{when }{Ca}_n > 0,\\ \beta_2 \approx{-}1.13 & \text{when }{Ca}_n < 0. \end{cases} \end{equation}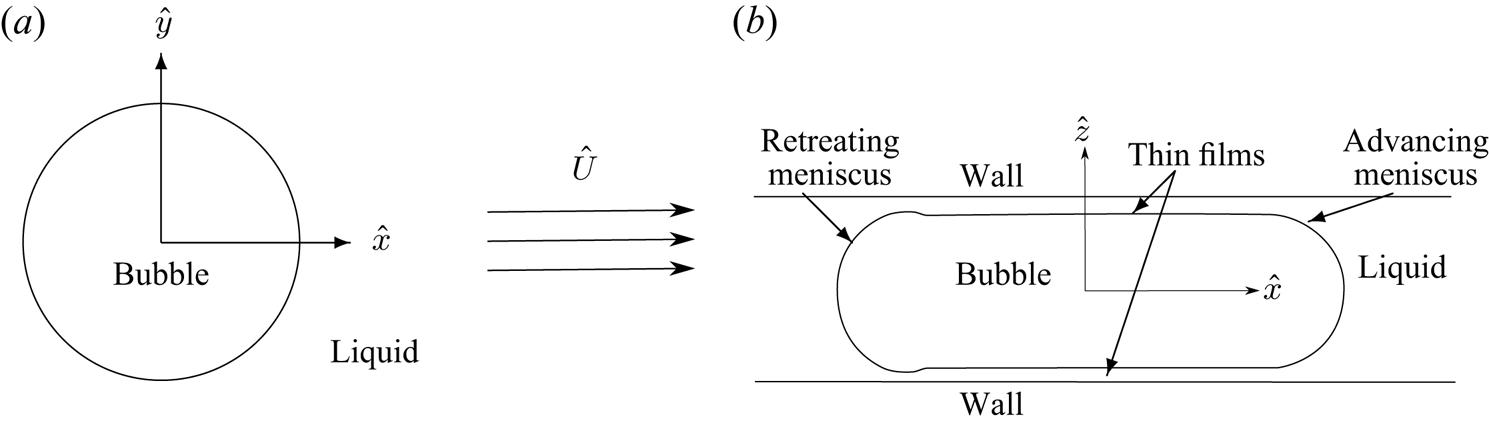

Figure 1. (a) Plan view of a bubble in a Hele-Shaw cell with a uniform background flow of speed $\hat {U}$. (b) Side view of the bubble.

The first term on the right-hand side of (2.3b) is the capillary pressure difference due to the meniscus at the bubble boundary, whose leading-order radius of curvature is given by $\hat {h}/2$. The second term, containing the capillary number, is the correction to the pressure difference in the limit ${Ca}_n\ll 1$, derived in Bretherton's original paper (Bretherton Reference Bretherton1961), due to the existence of the thin-film regions between the bubble and the walls of the cell (see figure 1b). The final term in (2.3b) captures the in-plane contribution to the curvature of the bubble interface, including the ${\rm \pi} /4$ factor derived by Park & Homsy (Reference Park and Homsy1984).

We will discuss further the underlying assumptions and validity of the boundary condition (2.3b) in § 4.

2.2. Non-dimensionalisation

We non-dimensionalise the model (2.1)–(2.3), scaling lengths with a typical bubble radius $\hat {R}$, and velocities with the far-field uniform flow speed $\hat {U}$. We also scale $\hat {p}$ with $12\hat {\mu }\hat {U}R/{\hat {h}}^2$, $\hat {p}_b$ with $2\hat {\gamma } / \hat {h}$, and $\hat {\kappa }$ with $1/\hat {R}$. This process yields the following dimensionless system (in which dimensionless variables are denoted without hats):

(2.5a)\begin{gather} \nabla^2 p = 0 \quad \mbox{in} \ \varOmega, \end{gather}

(2.5b)\begin{gather}p_b - \frac{3\,{Ca}}{\epsilon}\,p = 1 + {Ca}^{2/3}\,\beta(U_n)\,U_n^{2/3} + \frac{\epsilon {\rm \pi}}{4}\,\kappa \quad \mbox{on} \ \partial \varOmega_b, \end{gather}

(2.5c)\begin{gather}\boldsymbol{n}\boldsymbol{\cdot} \boldsymbol{\nabla} p={-} U_n \quad \mbox{on}\ \partial \varOmega_b, \end{gather}

(2.5d)\begin{gather}p\sim{-}x+o(1) \quad \text{as} \ x^2 +y^2 \rightarrow \infty, \end{gather}

where $\varOmega$ is the fluid domain, and $\partial \varOmega _b$ is the apparent bubble–fluid boundary in the $(x,y)$-plane, whose normal velocity is $U_n$. The far-field condition (2.5d) (with no logarithmic contribution) enforces conservation of the bubble area and thus in principle allows the bubble pressure $p_b$ to be determined as part of the solution.

The system (2.5) contains two dimensionless parameters, the aspect ratio and the capillary number, defined by

(2.6a,b)\begin{equation} \epsilon = \frac{\hat{h}}{2\hat{R}}, \quad {Ca} = \frac{\hat{\mu} \hat{U}}{\hat{\gamma}}, \end{equation}

respectively. For the boundary-value problem (2.5) to be valid, both of these parameters must be small: the Hele-Shaw model relies on $\epsilon$ being small, while the boundary condition (2.3b) is an asymptotic approximation in the limit ${Ca}\rightarrow 0$ (Park & Homsy Reference Park and Homsy1984). In the boundary condition (2.5b), the dominant balance depends on the relative size of these two small parameters.

In this work, we study flows in which the Hele-Shaw pressure is of the same order as the Bretherton drag term, and (2.5b) shows that this occurs when ${Ca} = O(\epsilon ^3)$. Expanding $p_b$ and $\kappa$ as asymptotic expansions in powers of $\epsilon$, we then see that

(2.7)\begin{align} p_{b_0}+\epsilon p_{b_1} + \epsilon^2 p_{b_2} -\underbrace{\frac{3\,{Ca}}{\epsilon}\,p}_{O (\epsilon^2)}\ +\ O(\epsilon^3) \sim 1 + \frac{\epsilon {\rm \pi}}{4}\, (\kappa_0+\epsilon\kappa_1) + \underbrace{\beta\,{Ca}^{2/3}\,U_n^{2/3}}_{O(\epsilon^2)}\ +\ O(\epsilon^3) \end{align}

on $\partial \varOmega _b$. At $O(1)$, we find that $p_{b_0} = 1$, indicating that the leading-order bubble pressure is determined by the capillary pressure jump across the meniscus. At $O(\epsilon )$, we obtain $\kappa _0=4p_{b_1}/{\rm \pi} = \text {const.}$, which implies that the bubbles that we are studying are circular to leading order in $\epsilon$. By our choice of length scale $\hat {R}$, we can take the bubble here to have unit dimensionless radius.

Since the bubble remains (approximately) circular for all time, the normal velocity on the boundary is just given by $U_n=\boldsymbol {U}_b\boldsymbol {\cdot }\boldsymbol {n}$, where $\boldsymbol {U}_b=(U_b,V_b)$ is the constant bubble velocity. In terms of plane polar coordinates $(r,\theta )$ based on the bubble centre, we therefore find that the pressure in the liquid satisfies the problem

(2.8a)\begin{gather} \nabla^2 p = 0 \quad \mbox{in} \ r>1, \end{gather}

(2.8b)\begin{gather}\frac{\partial p}{\partial r} ={-}\boldsymbol{U}_b\boldsymbol{\cdot}\boldsymbol{n}={-}U_b\cos\theta-V_b\sin\theta\quad \mbox{on} \ r=1, \end{gather}

(2.8c)\begin{gather}p\sim{-}r\cos\theta+o(1) \quad \text{as} \ r \rightarrow \infty. \end{gather}

If $\boldsymbol {U}_b$ were known, then $p$ would be uniquely determined by (2.8). To find the bubble velocity, we return to the boundary condition (2.7), which so far has been imposed up to $O(\epsilon )$. In principle, the solvability condition at $O(\epsilon ^2)$ determines $\boldsymbol {U}_b$ and closes the problem. As a shortcut to deriving this condition, we note that for any smooth closed planar curve $\partial \varOmega _b$ and with $\boldsymbol {k}$ denoting the unit vector in the $z$-direction,

(2.9a,b)\begin{equation} \oint_{\partial\varOmega_b} \boldsymbol{n} \, \mathrm{d}s= {\oint_{\partial\varOmega_b} \boldsymbol{k}\times\frac{\mathrm{d}\boldsymbol{r}}{\mathrm{d}s} \, \mathrm{d}s= \boldsymbol{0},\quad} \oint_{\partial\varOmega_b} \kappa \boldsymbol{n} \, \mathrm{d}s = \oint_{\partial\varOmega_b} -\frac{\mathrm{d}^2\boldsymbol{r}}{\mathrm{d}s^2} \, \mathrm{d}s= \boldsymbol{0}, \end{equation}

by standard results from differential geometry (see e.g. Kreyszig Reference Kreyszig1959, Chapter 2). We therefore obtain from (2.5b) the constraint

(2.10)\begin{equation} \oint_{\partial\varOmega_b} -p\boldsymbol{n}\, \mathrm{d}s = \frac{\epsilon}{3\,{Ca}^{1/3}} \oint_{\partial\varOmega_b} \beta (\boldsymbol{U}_{b} \boldsymbol{\cdot} \boldsymbol{n})\,(\boldsymbol{U}_{b} \boldsymbol{\cdot} \boldsymbol{n})^{2/3}\boldsymbol{n}\, \mathrm{d}s, \end{equation}

which may be interpreted as a force balance on the bubble. To evaluate the integral on the right-hand side of (2.10), we now use the fact that, to leading order, the boundary $\partial \varOmega _b$ is the unit circle, which we parametrise using

(2.11a)\begin{equation} \boldsymbol{r}(s)=\frac{\boldsymbol{U}_b}{|\boldsymbol{U}_b|}\cos s +\frac{\boldsymbol{k}\times\boldsymbol{U}_b}{|\boldsymbol{U}_b|}\sin s. \end{equation}

With $\beta$ given by (2.4), we thus obtain

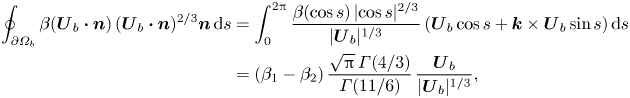(2.11b)\begin{align} \oint_{\partial\varOmega_b} \beta (\boldsymbol{U}_{b} \boldsymbol{\cdot} \boldsymbol{n})\,(\boldsymbol{U}_{b} \boldsymbol{\cdot} \boldsymbol{n})^{2/3}\boldsymbol{n}\, \mathrm{d}s &= \int_0^{2{\rm \pi}} \frac{\beta(\cos s)\,|{\cos s}|^{2/3}}{|\boldsymbol{U}_b|^{1/3}} \left(\boldsymbol{U}_b\cos s+\boldsymbol{k}\times\boldsymbol{U}_b\sin s\right)\mathrm{d}s\nonumber\\ &=(\beta_1-\beta_2)\,\frac{\sqrt{\rm \pi}\,\varGamma(4/3)}{\varGamma(11/6)}\, \frac{\boldsymbol{U}_b}{|\boldsymbol{U}_b|^{1/3}}, \end{align}

where $\varGamma$ denotes the gamma function. Thus (2.10) reduces to the following condition for the bubble velocity:

(2.12)\begin{equation} \frac{\boldsymbol{U}_b}{|\boldsymbol{U}_b|^{1/3}} =\frac{\delta}{\rm \pi}\oint_{r=1} -p\boldsymbol{n}\, \mathrm{d}s, \end{equation}

where we define the Bretherton parameter

(2.13)\begin{equation} \delta = \frac{3\sqrt{\rm \pi}\,\varGamma(11/6)}{(\beta_1 - \beta_2)\,\varGamma(4/3)}\, \frac{{Ca}^{1/3}}{\epsilon} \approx 1.12\,\frac{{Ca}^{1/3}}{\epsilon}. \end{equation}

By assumption, $\delta$ is $O(1)$ while $\epsilon$ and ${Ca}$ are asymptotically small.

2.3. Solution

The problem (2.8) for an isolated circular bubble in an infinite cell is easily solved to obtain the pressure

(2.14)\begin{equation} p = \left(\frac{U_b -1}{r}-r\right)\cos\theta + \frac{V_b}{r}\sin\theta. \end{equation}

We can thus evaluate the integral on the right-hand side of the force balance (2.12) to obtain an equation for the bubble velocity, namely

(2.15)\begin{equation} \frac{\boldsymbol{U}_b}{|\boldsymbol{U}_b|^{1/3}}=\delta(2\boldsymbol{i}-\boldsymbol{U}_b). \end{equation}

It follows that the bubble moves parallel to the background flow, as expected, with $\boldsymbol {U}_b=U_b\boldsymbol {i}$, where $U_b$ satisfies the algebraic equation

(2.16)\begin{equation} \frac{U_b^{2/3}}{2-U_b}=\delta.\end{equation}

The equation (2.16) for the bubble speed is equivalent to that found in Reichert et al. (Reference Reichert, Cantat and Jullien2019), using a laborious viscous dissipation argument. (In Reichert et al. (Reference Reichert, Cantat and Jullien2019), the constant of proportionality in (2.13) is found to be 1.20 rather than 1.12, due to inaccurate calculation of the integral and the Bretherton constants. Their method involves solution for the height of the thin liquid films above and below the bubble, followed by calculation of the viscous dissipation due to the thin films.) We note that (2.16) may be transformed into a cubic and thus solved explicitly for $U_b$; however, the resulting expression is unwieldy and not particularly illuminating.

We plot the prediction (2.16) for the bubble velocity $U_b$ versus the Bretherton parameter $\delta$ in figure 2, which shows good agreement with experimental data taken from Reichert et al. (Reference Reichert, Cantat and Jullien2019) and Park et al. (Reference Park, Maruvada and Yoon1994). We observe that $U_b$ is an increasing function of $\delta$; from (2.13), we see that $\delta$ is proportional to the bubble radius $\hat {R}$, which implies that larger bubbles should travel faster. As $\delta \rightarrow 0$, the Bretherton drag term dominates and $U_b \sim (2\delta )^{3/2}$. At the other extreme, where $\delta \gg 1$, we recover the traditional Taylor–Saffman result (Taylor & Saffman Reference Taylor and Saffman1959) of the bubble moving twice as fast as the outer flow. However, we note that the assumption of the bubble remaining approximately circular eventually fails if $\delta$ is too large. From (2.7), we observe that variations in the bubble curvature are of order $\delta ^2\epsilon$, which is assumed to be small. We conclude that our model remains valid when $\delta$ is large, provided that $1\ll \delta \ll \epsilon ^{-1/2}$.

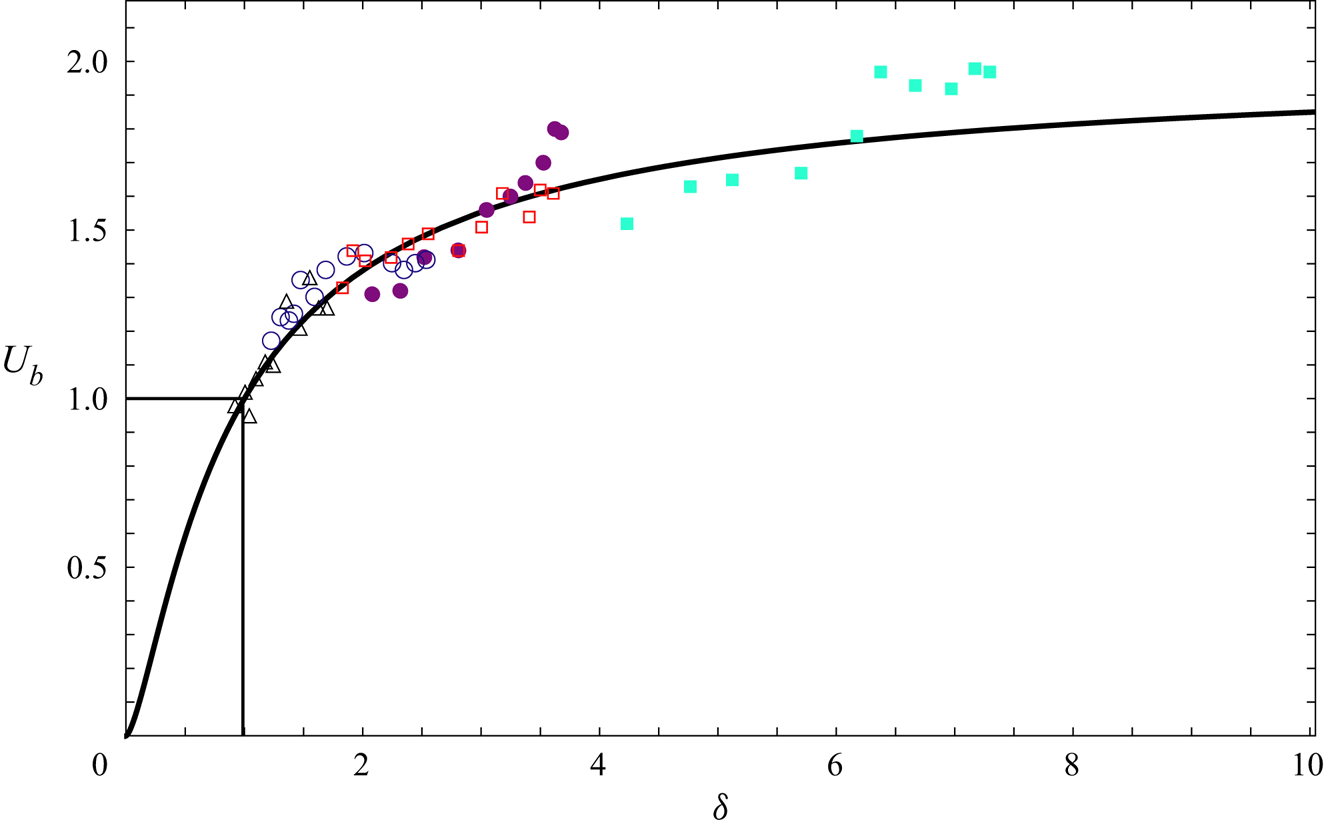
Figure 2. The ratio $U_b$ of the bubble velocity to the outer fluid velocity as a function of the Bretherton parameter $\delta$. The solid curve shows the model prediction (2.16). The points show experimental data: cyan solid squares ($\epsilon =0.035$) and maroon solid dots ($\epsilon = 0.071$) from Park et al. (Reference Park, Maruvada and Yoon1994), with ${Ca}$ in the range $2.3\unicode{x2013}12.7\times 10^{-3}$; red squares ($\epsilon = 0.044)$, blue circles ($\epsilon = 0.07$) and grey triangles ($\epsilon = 0.091$) from Reichert et al. (Reference Reichert, Cantat and Jullien2019), with ${Ca}$ in the range $0.4\unicode{x2013}6.0\times 10^{-3}$.

From (2.16), we observe a transition in behaviour at $\delta = 1$: if $\delta < 1$, then the bubble moves slower than the outer flow ($U_b<1)$, while if $\delta > 1$, then the bubble moves faster than the outer flow ($U_b>1)$. The critical case where $U_b=1$, so the bubble moves with the external flow, corresponds to the particular solution of the problem where $p \equiv -x$. We see that this solution satisfies (2.8) provided that $(U_b,V_b) = (1,0)$, and the force balance (2.12) is also satisfied provided that $\delta = 1$.

2.4. The $N$-bubble problem

It is straightforward to generalise the model derived above to describe a system of $N$ bubbles. For the moment, we continue to treat the Hele-Shaw cell containing the bubbles as effectively infinite, with a uniform flow imposed at infinity; the effects of cell boundaries will be incorporated below.

As in § 2.2, each bubble remains circular (to leading order), with dimensionless radius $R_k$ and velocity $\boldsymbol {U}_k$, say, for $1\leqslant k\leqslant N$. The dimensionless pressure in the liquid domain $\varOmega$ therefore satisfies

(2.17a)\begin{gather} \nabla^2 p = 0 \quad \text{in} \ \varOmega, \end{gather}

(2.17b)\begin{gather}\boldsymbol{n}\boldsymbol{\cdot}\boldsymbol{\nabla} p ={-}\boldsymbol{U}_{k} \boldsymbol{\cdot} \boldsymbol{n} \quad\text{on} \ \partial\varOmega_{k}, \end{gather}

(2.17c)\begin{gather}\boldsymbol{\nabla}p\rightarrow-\boldsymbol{i} \quad \text{as} \ x^2 +y^2 \rightarrow \infty, \end{gather}

where $\partial \varOmega _{k}$ denotes the (circular) boundary of the $k\text {th}$ bubble. In principle, $p$ would thus be determined if we knew the velocity $\boldsymbol {U}_k$ of each bubble. Indeed, the boundary-value problem described in (2.17) would then be equivalent to finding the velocity potential exterior to a collection of moving bodies or stirrers in two-dimensional irrotational flow with no circulation. The two-body version of this problem has been solved by Tchieu, Crowdy & Leonard (Reference Tchieu, Crowdy and Leonard2010), and general integral expressions for the velocity potential due to any finite number of moving bodies are given by Crowdy (Reference Crowdy2008).

In the present problem, however, the bubble velocities are not known in advance. As in § 2.2, the required equation of motion is obtained by performing an effective force balance, which here leads to

(2.18)\begin{equation} \frac{\boldsymbol{U}_k}{|\boldsymbol{U}_k|^{1/3}} =\frac{\delta}{{\rm \pi} R_k}\oint_{\partial\varOmega_k} -p\boldsymbol{n}\, \mathrm{d}s. \end{equation}

Again we notice that $p = -x$ is a solution to the problem (2.17) if and only if all of the bubbles move at the same velocity $\boldsymbol {U}_k =\boldsymbol {i}$ for all $k$. The force balance (2.18) then requires $\delta R_k=1$. Therefore, it is possible for all of the bubbles to be convected at the same velocity as the outer flow, regardless of their position, only when all the bubbles are the same size.

Thus far we have formulated a general model for the motion of approximately circular bubbles in a Hele-Shaw cell, and solved the model explicitly for the simplest possible case of a single isolated bubble. In the next section, we use the model to analyse some more complicated examples, which illustrate the effects of walls on the bubble motion and the interactions between multiple bubbles.

3.1. Isolated bubble near a wall

Next, we consider the case of a single bubble in a semi-infinite Hele-Shaw cell ($y>0$) with an impermeable wall at $y=0$ and a uniform flow $-\boldsymbol {\nabla }p\sim \boldsymbol {i}$ at infinity. The bubble is taken to have unit dimensionless radius, with its centre a dimensionless distance $a>1$ away from the boundary. The following analysis allows us to examine how proximity to a wall affects the velocity of the bubble, and also illustrates the application of complex variable methods to our model. This formulation is equivalent to the problem of two identical bubbles in an infinite cell with their centres separated by $2a$ and lined up perpendicular to the outer flow direction, with the wall representing the line of symmetry between them. The corresponding two-bubble problem was solved by Sarig et al. (Reference Sarig, Starosvetsky and Gat2016) using bipolar coordinates rather than complex variables. We choose the bubble centre to be instantaneously at $z = x+\mathrm {i}y=a\mathrm {i}$, so that the domain of interest is $\varOmega =\{z: \operatorname {Im}(z)>0, |z-a\mathrm {i}|>1\}$.

Since $p$ satisfies Laplace's equation, we introduce a complex potential $w(z) = -p + \mathrm {i}\psi$, where $\psi$ is the streamfunction. The problem is then to find a holomorphic function $w(z)$ in the region $\varOmega$ such that

(3.1a)\begin{gather} \operatorname{Im}[w(z)] = 0 \quad \text{on} \ \operatorname{Im}(z) = 0, \end{gather}

(3.1b)\begin{gather}\operatorname{Im}[w(z)] = q +\operatorname{Im}\left[\bar{\mathcal{U}}_bz\right] \quad\text{on} \ |z-a\mathrm{i}|=1, \end{gather}

(3.1c)\begin{gather}w(z) \sim z \quad\text{as} \ z \rightarrow \infty {.} \end{gather}

Both the complex bubble velocity $\mathcal {U}_b=U_b+\mathrm {i}V_b$ and the real constant $q$ are a priori unknown; $q$ represents the flux of liquid through the gap between the bubble and the wall (relative to the moving bubble). Once we have solved for $w$, the equation of motion (2.12) may be imposed by evaluating

(3.2)\begin{equation} \frac{1}{\mathrm{i}{\rm \pi}}\oint_{\partial\varOmega_b} w(z)\,\mathrm{d}z={-}\mathcal{U}_b+\frac{1}{\rm \pi}\oint_{\partial\varOmega_b}p\mathrm{i}\,\mathrm{d}z ={-}\mathcal{U}_b+\frac{\mathcal{U}_b}{\delta\left|\mathcal{U}_b\right|^{1/3}}. \end{equation}

We proceed by conformally mapping $\varOmega$ onto a concentric annulus, where the problem becomes solvable with standard techniques. Following the mapping

(3.3)\begin{equation} \zeta = f(z) = \frac{z-\mathrm{i}\sqrt{a^2-1}}{z+\mathrm{i}\sqrt{a^2-1}}, \end{equation}

the solution domain in the $\zeta$-plane is $A=\{\zeta :X<|\zeta |<1\}$, where

(3.4)\begin{equation} X =a-\sqrt{a^2-1}. \end{equation}

Writing the complex potential in the form $w(z)= z+W(f(z))$, we find that $W$ is holomorphic on $A$ and satisfies the boundary conditions

(3.5a)\begin{gather} \operatorname{Im}[W(\zeta)] = 0 \quad \text{on} \ |\zeta| = 1, \end{gather}

(3.5b)\begin{gather}\operatorname{Im}[W(\zeta)] = q- \operatorname{Im}\left[\alpha\left(\frac{ 1+\zeta}{1-\zeta}\right)\right] \quad\text{on}\ |\zeta| = X, \end{gather}

where $\alpha = (1-\bar {\mathcal {U}}_b)\mathrm {i}\sqrt {a^2-1}$.

We then find that the a priori unknown flux $q$ is given by

(3.6)\begin{equation} q=\operatorname{Im}(\alpha)= (1-U_b)\sqrt{a^2-1}, \end{equation}

and the complex potential in the $\zeta$-plane is given by

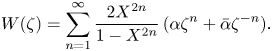(3.7)\begin{equation} W(\zeta) = \sum_{n=1}^{\infty}\frac{2 X^{2n}}{1 - X^{2n}}\,(\alpha\zeta^n+\bar{\alpha}\zeta^{{-}n}). \end{equation}

We can thus calculate the integral on the left-hand side of (3.2) by transforming into the $\zeta$-plane and then using Cauchy's residue theorem to obtain

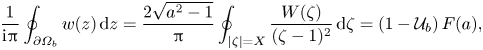(3.8)\begin{equation} \frac{1}{\mathrm{i}{\rm \pi}}\oint_{\partial\varOmega_b} w(z) \, \mathrm{d}z = \frac{2\sqrt{a^2 -1}}{\rm \pi}\oint_{|\zeta| = X} \frac{W(\zeta)}{(\zeta -1)^2} \, \mathrm{d}\zeta = (1-\mathcal{U}_b)\,F(a), \end{equation}

where

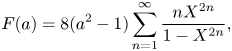(3.9)\begin{equation} F(a)=8(a^2-1)\sum_{n=1}^{\infty} \frac{n X^{2n}}{1 - X^{2n}}, \end{equation}

with $X$ given as a function of $a$ by (3.4). The formula (3.9) may be written in closed form as

(3.10)\begin{equation} F(a) = 2(a^2 -1)\,\frac{\varPsi_{X^2}'(1)}{\log^2X}, \end{equation}

in which $\varPsi _{X^2}$ denotes the $q$-digamma function (Salem Reference Salem2012), defined by

(3.11)\begin{equation} \varPsi_q (z)= \frac{1}{\varGamma_q (z)}\,\frac{\mathrm{d}\varGamma_q (z)}{\mathrm{d}z}, \end{equation}

where $\varGamma _q$ is the $q$-gamma function (Askey Reference Askey1978). As shown in figure 3, $F(a)$ is a decreasing function of $a$, with $F(1) = {\rm \pi}^2 /3$ and $F(a) \rightarrow 2$ as $a\rightarrow \infty$.

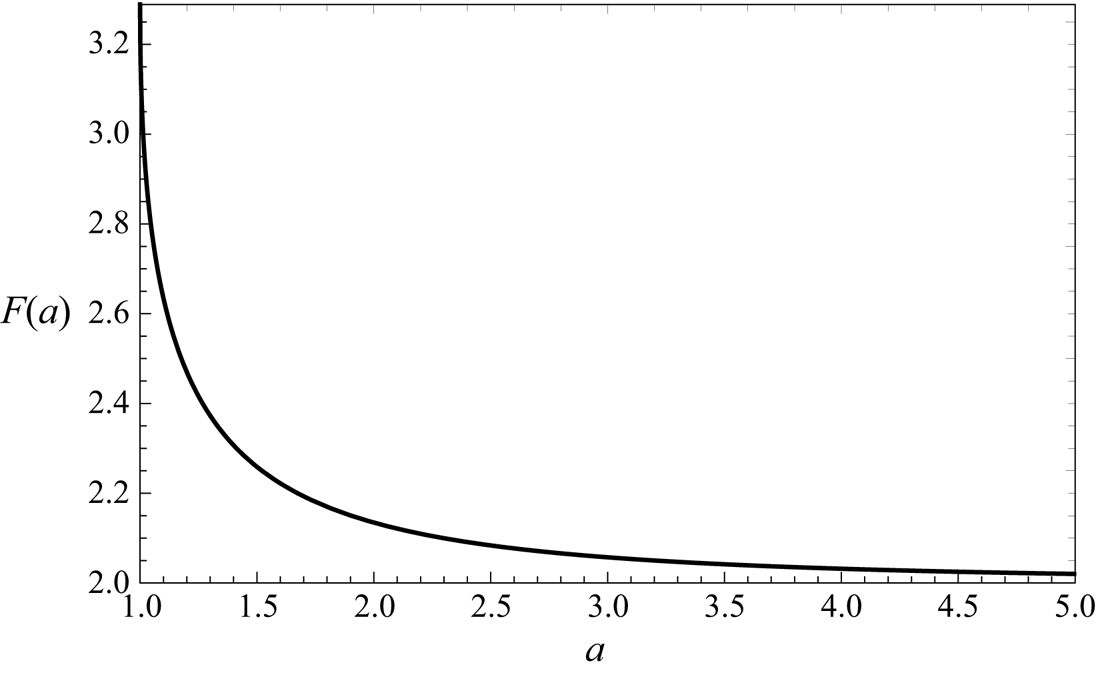
Figure 3. The function $F(a)$ defined by (3.10).

Comparing imaginary parts in (3.2), we find that $V_b = 0$, so the bubble moves parallel to the wall. Then equating real parts in (3.2), the bubble's velocity in the $x$-direction is found to satisfy the algebraic equation

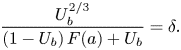(3.12)\begin{equation} \frac{U_b^{2/3} }{ (1-U_b)\,F(a)+U_b}= \delta. \end{equation}

Once again, (3.12) gives us a cubic that in principle can be solved explicitly for the dimensionless bubble velocity $U_b$. Rather than writing this complicated expression out explicitly, below we briefly examine the possible limiting cases.

First, we observe that $U_b =1$ when $\delta = 1$, so the bubble moves precisely with the external flow at this same critical value of the Bretherton parameter, regardless of the distance from the wall. As noted in § 2.3, this special case corresponds to the particular solution where $p = -x$. For the extreme values of the Bretherton parameter $\delta$, using (3.12) we derive the limits

(3.13a)\begin{gather} U_b \rightarrow \frac{F(a)}{F(a)-1} \quad\text{as}\ \delta \rightarrow \infty, \end{gather}

(3.13b)\begin{gather}U_b \sim \left(\delta\,F(a)\right)^{3/2} \quad\text{as}\ \delta \rightarrow 0. \end{gather}

Taking the derivative of (3.12) with respect to $\delta$, we find

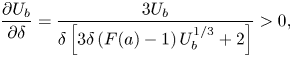(3.14)\begin{equation} \frac{\partial U_b}{\partial \delta} =\frac{3U_b}{\delta\left[3\delta\left(F(a)-1\right)U_b^{1/3}+2\right]}>0, \end{equation}

so $U_b$ is a strictly increasing function of $\delta$. It follows that $U_b >1$ when $\delta > 1$, and vice versa.

As noted above, $F(a) \rightarrow 2$ as $a \rightarrow \infty$, so in this limit, (3.12) reduces to the result (2.16) for a bubble in an infinite fluid medium, as expected. Similarly, we can look at the limit $a\rightarrow 1$ in which the bubble touches the wall. Since $F(1) = {\rm \pi}^2 / 3$, the bubble velocity tends to a non-zero value, which depends on the Bretherton parameter through the relation

(3.15)\begin{equation} \frac{3U_b^{2/3}}{{\rm \pi}^2 - ({\rm \pi}^2 -3)U_b}=\delta. \end{equation}

For intermediate values of $a$, we find that

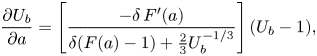(3.16)\begin{equation} \frac{\partial U_b}{\partial a} = \left[\frac{-\delta\,F'(a)}{\delta(F(a)-1)+\frac{2}{3} U_b^{{-}1/3}}\right](U_b-1), \end{equation}

in which the term in square brackets is positive. It follows that $U_b$ is a decreasing function of $a$ when $\delta < 1$, but an increasing function of $a$ when $\delta > 1$.

The behaviour of the bubble velocity as the parameters $a$ and $\delta$ are varied is shown in figure 4. As predicted, we observe that the presence of the wall either increases or decreases the bubble velocity, depending on whether $\delta <1$ or $\delta >1$, respectively. At the critical value $\delta = 1$, we have $U_b =1$ and the distance from the wall no longer matters.

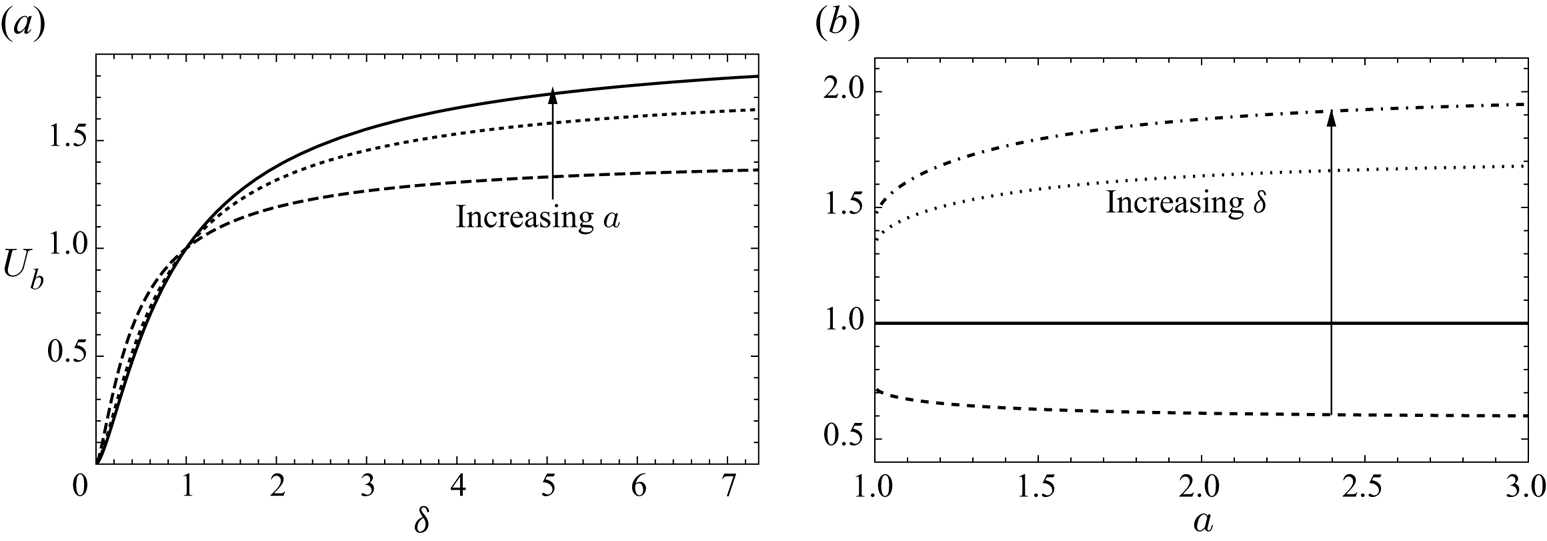
Figure 4. (a) Bubble velocity $U_b$ versus Bretherton parameter $\delta$ for $a = 1$ (dashed), $a = 1.5$ (dotted) and $a = \infty$ (solid). (b) Bubble velocity $U_b$ versus distance $a$ from the wall for Bretherton parameter $\delta = 1/2$ (dotted), $\delta = 1$ (solid), $\delta = 5$ (dashed) and $\delta = \infty$ (dot-dashed).

At first glance, it appears paradoxical that proximity to the wall may cause the bubble to either speed up or slow down, depending on the size of $\delta$, but the behaviour may be explained as follows. By using the boundary condition (2.17b) and integration by parts, the force balance (2.18) may be rewritten as

(3.17)\begin{equation} \boldsymbol{U}_b\left(1+ \frac{1}{\delta\,|\boldsymbol{U}_b|^{1/3}}\right) =\frac{1}{\rm \pi}\oint_{\partial\varOmega_b} \boldsymbol{u}\, \mathrm{d}s, \end{equation}

where $\boldsymbol {u}=(u,v)^{\text {T}}=-\boldsymbol {\nabla }p$ is the dimensionless liquid velocity. For an isolated bubble, with the pressure given by (2.14), the integral on the right-hand side of (3.17) is easily calculated to be $2\boldsymbol {i}$, reproducing the equation of motion (2.15), and in general this term captures the influence of the outer flow on the bubble motion.

Now, what happens when a wall is introduced next to the moving bubble? From (3.6), we can calculate the average flow speed through the gap between the bubble and the wall (relative to the moving bubble) as

(3.18)\begin{equation} \frac{1}{a-1}\int_0^{a-1}(u-U_b)\,\mathrm{d} y= \frac{q}{a-1}=(1-U_b)\,\sqrt{\frac{a+1}{a-1}}. \end{equation}

First, suppose that the bubble is moving more slowly than the external flow, so $U_b<1$. The right-hand side of (3.18) increases as the separation $a-1$ between the bubble and the wall decreases, measuring the acceleration of the liquid as it squeezes between the bubble and the wall. We find that the average velocity on the bubble surface thus increases and, according to (3.17), the bubble velocity also increases (relative to an isolated bubble). The horizontal component of the right-hand side of (3.17) may be calculated as

(3.19)\begin{equation} \frac{1}{\rm \pi}\oint_{\partial\varOmega_b}u\,\mathrm{d}s =2+(1-U_b)\left(F(a)-2\right), \end{equation}

which indeed increases as $a$ decreases when $U_b<1$.

On the other hand, if the bubble moves more quickly than the external flow ($U_b>1$), then the liquid is squeezed backwards through the gap between the bubble and the wall so, by the same argument, the integral on the right-hand side of (3.17) and the bubble velocity should both decrease. This physical reasoning indeed agrees with the behaviour observed in figure 4. As noted above, the bubble travels faster or slower than the external flow depending on whether $\delta <1$ or $\delta >1$, and the effect of proximity to the wall is accordingly either to speed up or to slow down the bubble.

3.2. Isolated bubble in a channel

Next, we consider the motion of a singular bubble of unit radius in a Hele-Shaw channel of width $W>2$, between impermeable walls at $y=\pm W/2$. We again impose a uniform flow with $p\sim -x$ at infinity and, without loss of generality, take the bubble centre to be instantaneously at $(x,y) = (0,y_b)$, where $|y_b|< W/2-1$. It may then be shown that $p$ is an odd function of $x$, and it follows from (2.12) that $V_b = 0$. Thus a single bubble in a channel will continue moving parallel to the outer flow no matter where in the channel it is initially placed.

To facilitate numerical solution, we pose the problem in terms of the streamfunction $\psi$, which satisfies Dirichlet boundary conditions

(3.20a)\begin{gather} \psi(x,y)={\pm}\frac{W}{2} \quad\text{at}\ y={\pm}\frac{W}{2}, \end{gather}

(3.20b)\begin{gather}\psi(x,y)=q+U_b y \quad \text{at}\ x^2+(y-y_b)^2=1, \end{gather}

(3.20c)\begin{gather}\psi(x,y)\rightarrow y \quad \text{as}\ x\rightarrow\pm\infty. \end{gather}

The a priori unknown constant $q$ is in principle determined by the constraint

(3.21)\begin{equation} \oint_{\partial\varOmega_b}\frac{\partial\psi}{\partial n}\,\mathrm{d}s=0, \end{equation}

which follows from single-valuedness of the pressure. The streamfunction is then decomposed as $\psi =U_b y+(1-U_b)\psi _1+q\psi _2$, where each $\psi _k$ satisfies a normalised boundary-value problem that is independent of $q$ and $U_b$. We solve for $\psi _1$ and $\psi _2$ using finite element methods, and then compute the four integrals

(3.22a)$$\begin{gather} I_k=\frac{1}{\rm \pi}\oint_{\partial\varOmega_b}\left(\frac{\partial\psi_k}{\partial x}\,\mathrm{d}y- \frac{\partial\psi_k}{\partial y}\,\mathrm{d} x\right), \end{gather}$$

(3.22b)$$\begin{gather}J_k=\frac{1}{\rm \pi}\oint_{\partial\varOmega_b}\left(x\,\frac{\partial\psi_k}{\partial x}+(y-y_b)\,\frac{\partial\psi_k}{\partial y}\right)\mathrm{d} x \end{gather}$$

($k=1,2$). The force balance (2.12) and constraint (3.21) provide two algebraic equations for $q$ and $U_b$. As in § 3.1, the resulting equation of motion may be expressed in the form

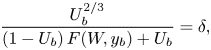(3.23)\begin{equation} \frac{U_b^{2/3}}{(1-U_b)\,F(W,y_b)+U_b}=\delta, \end{equation}

where now $F(W,y_b)=J_2I_1/I_2-J_1$. For given values of $W$ and $y_b$, the value of $F(W,y_b)$ can be computed once-and-for-all, following the procedure described above, and the dependence of $U_b$ on $\delta$ is then determined by (3.23). An analogous approach is used to compute the numerical solutions with multiple bubbles below.

We start by considering a bubble travelling along the centreline of the channel, with $y_b=0$, in which case it is easy to see that $q$ must also equal zero. Hence $F(W,0)=-J_1$, and the one remaining integral can in principle be calculated using a Schwarz–Christoffel mapping (Anselmo et al. Reference Anselmo, Nelson, Carneiro da Cunha and Crowdy2018) or approximation schemes described by Crowdy (Reference Crowdy2016) and Love (Reference Love1938), for example.

In figure 5(a), we examine the effects of varying the channel width $W$ and Bretherton parameter $\delta$. We observe that $U_b$ is an increasing function of $\delta$, and as $\delta \rightarrow \infty$, it tends to a value strictly less than the Taylor–Saffman value $U_b=2$. Again $\delta = 1$ is the critical value where the bubble moves with the external flow independently of the channel width, corresponding to the exact solution of the problem where $p=-x$. As in § 3.1, the bubble may be accelerated or retarded by the presence of walls, depending on whether $\delta <1$ or $\delta >1$, respectively. In the limit of large $W$, the solution approaches that for an isolated bubble, as expected, while the solutions all converge to $U_b=1$ as $W\rightarrow 2$. This latter limit corresponds to the case when the bubble exactly fits the channel width and, by conservation of mass, must travel at the same speed as the outer flow.

Figure 5. Bubble velocity $U_b$ versus: (a) channel width $W$, with offset $y_b=0$; (b) distance $W/2-1-y_b$ from the top channel wall, with width $W=4$ and offset $y_b\in [0,1]$. Here, the Bretherton parameter is $\delta =1/2$ (dashed), $\delta =1$ (solid), $\delta = 5$ (dotted) and $\delta = \infty$ (dot-dashed).

In figure 5(b), we study the effects of the bubble being off-centre in the channel by fixing $W=4$ and varying $y_b$. Again we observe that proximity to a wall may either increase or decrease the bubble velocity, depending on whether $\delta < 1$ or $\delta > 1$, respectively, with $\delta =1$ the critical case where $U_b=1$ for all $y_b$. As in § 3.1, this behaviour is caused by the liquid flowing through the gaps between the bubble and the channel walls, which either speeds up or slows down, thereby increasing or decreasing the average velocity at the bubble surface in (3.17).

3.3. Two identical bubbles in a channel

Next, we examine a system of two identical bubbles travelling along the centreline of the channel. Without loss of generality, we take the centres of the two bubbles to be initially at $\pm (1+S/2,0)$, where $S$ is the bubble separation. By symmetry, one can then show that the bubbles must both move along the centreline with identical velocities $\boldsymbol {U}_1=\boldsymbol {U}_2=(U_b,0)$.

In figure 6, we show that the two-bubble solution converges rapidly to the corresponding one-bubble solution as we increase the separation between the two bubbles, with the solutions matching up very closely even for $S=2$. For $\delta <1$, the bubble pair moves more slowly than a single bubble, but for $\delta >1$, it moves more quickly. In other words, the acceleration or retardation of the liquid as it squeezes through the gaps between each bubble and the channel walls (as described in §§ 3.1 and 3.2) is suppressed by the presence of the other bubble.

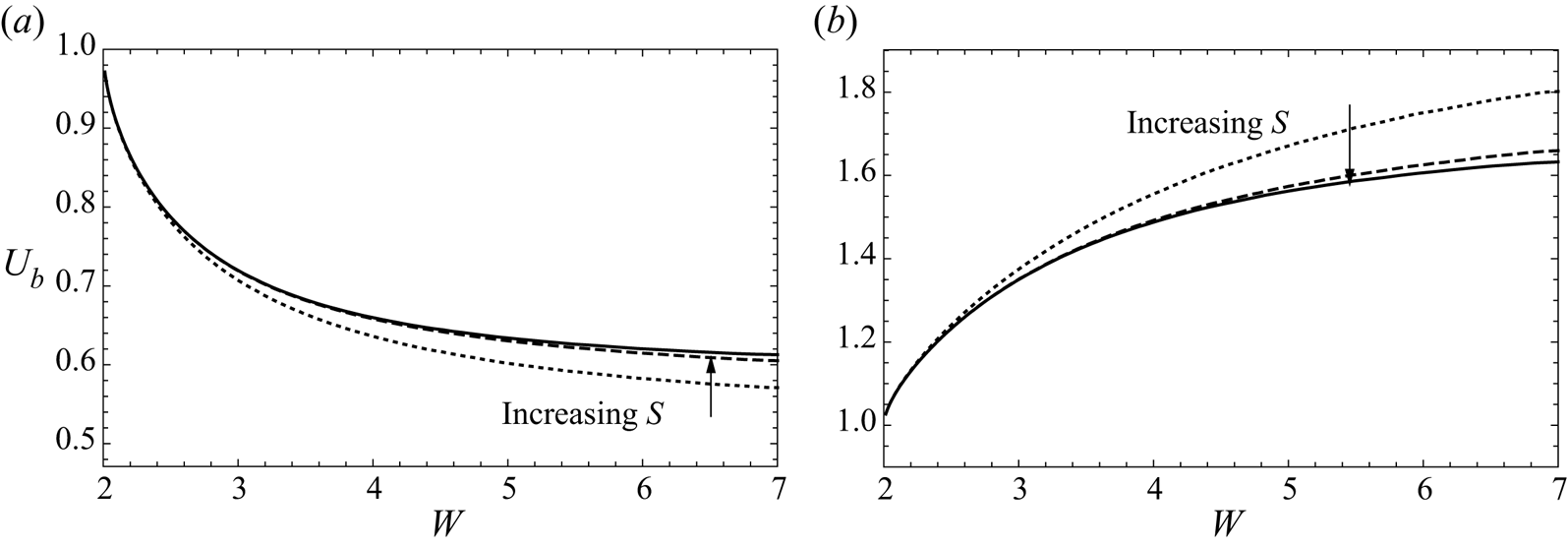
Figure 6. Bubble velocity $U_b$ versus channel width $W$ for a two-bubble system with separation $S = 0.2$ (dotted), $S = 2$ (dashed), single-bubble solution (solid), and (a) $\delta = 1/2$, (b) $\delta =5$.

3.4. A Hele-Shaw Newton's cradle

With three identical bubbles moving along the centreline of a channel, we find that the bubbles in general have different speeds so, for the first time, we have to solve an unsteady problem. At each time step, we compute the three instantaneous bubble speeds by following an approach similar to that described in § 3.2, and then update the bubble positions. We again see different behaviour depending on whether $\delta <1$ or $\delta >1$.

At the special value $\delta =1$, all of the bubbles move with the background flow, so the distances between them remain fixed. When $\delta < 1$, the bubbles move more slowly than the surrounding liquid. In this case, we recall from § 3.3 that the bubbles’ speed is increased by confinement from the channel walls but decreased by the presence of a second bubble. When there are three bubbles, we find that the outer two bubbles shield the middle one from the accelerating influence of the walls. We therefore observe that the centre bubble moves backwards relative to the outer two, and thus eventually becomes a pair with the rear bubble (see figure 7a). This qualitative behaviour has been observed experimentally by Shen et al. (Reference Shen, Leman, Reyssat and Tabeling2014); however, there were surfactants in their system so a quantitative comparison with our model is not possible. The opposite effect occurs when $\delta >1$, where now the central bubble moves faster than the outer ones and so eventually joins with the front bubble (see figure 7b).

Figure 7. The progression of a series of three identical bubbles, with (a) $\delta =1/2$, (b) $\delta =5$.

Figure 8 depicts the dependence on $\delta$ of the time $T$ taken for the middle bubble either to be caught by the rear bubble or to catch the front bubble. The initial bubble separations are set to $1$ and $0.04$, as shown in figure 7(a) for $\delta <1$ and figure 7(b) for $\delta >1$, and we show the results for two channel widths, $W=4$ and $W=20$. We see an asymptote at $\delta =1$, as expected when all the bubbles travel at the outer fluid speed. There is also an asymptote as $\delta \rightarrow 0$, since the bubble velocities all tend to zero in this limit. As $\delta \rightarrow \infty$, $T$ approaches a finite non-zero value that depends on $W$. Furthermore, we observe that $T$ increases as we decrease the channel width, with $T\rightarrow \infty$ as $W\rightarrow 2$ for all values of $\delta$, again because the bubbles all move at the same speed in this limit, by conservation of mass. Even at $W=4$, the transit time is quite large for all values of $\delta$, indicating that the difference in speed between the bubbles is relatively small.

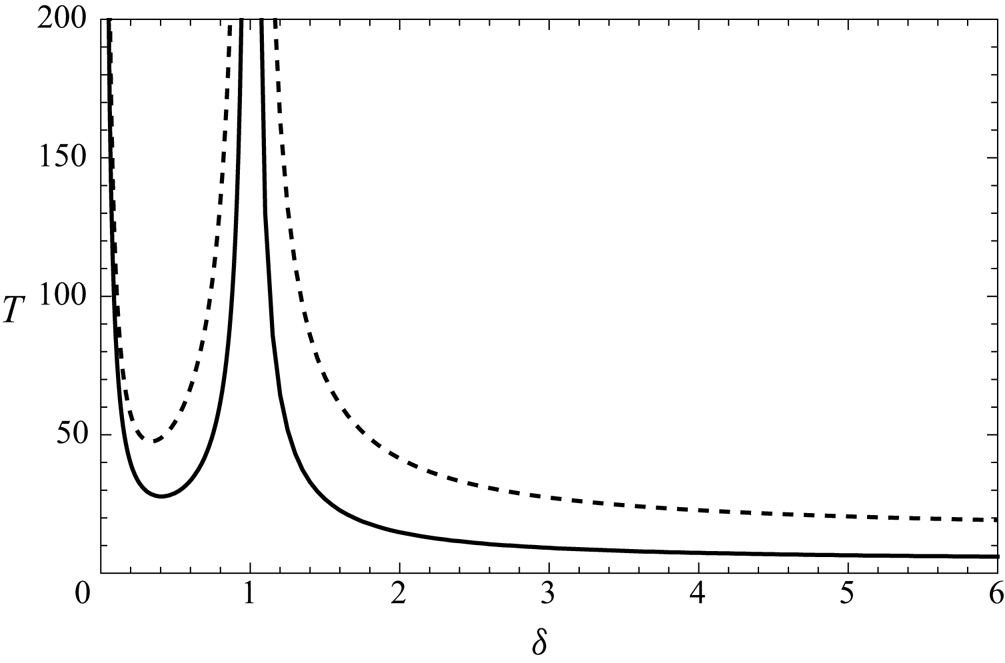
Figure 8. The transit time $T$ versus Bretherton parameter $\delta$ for the system shown in figure 7(a) for $\delta <1$ and figure 7(b) for $\delta >1$, in a channel of width $W=20$ (solid) and $W=4$ (dashed). When $\delta <1$, the computation starts with separations of $1$ and $0.04$ between the rear two and front two bubbles, respectively, and finishes when the separation between the rear two bubbles is $0.04$; and vice versa when $\delta >1$.

When there are more than three bubbles, this effect can occur multiple times, as illustrated in figure 9(a) for a case with $\delta <1$. Initially, the second bubble breaks away from the front one to form a pair with the third bubble, before that pair itself breaks up so the third and fourth bubbles can form a pair. For $\delta <1$, we recall from § 3.3 that a pair of bubbles moves more slowly than an isolated bubble, so for longer times, the trailing pair in figure 9(a) is left behind by the front two. Beatus et al. (Reference Beatus, Bar-Ziv and Tlusty2012) observed qualitatively similar longitudinal waves propagating backwards relative to the outer fluid flow in a series of bubbles on the centreline of a Hele-Shaw channel, which behaviour they termed the peloton effect. However, we find that the wave propagation can occur in either direction, depending on whether $\delta <1$ or $\delta >1$. Figure 9(b) shows a typical case with $\delta >1$, where the initial condition is the reverse of that in figure 9(a), and the observed evolutions are almost mirror images of each other. When $\delta >1$, a pair of bubbles travels faster than an isolated bubble, so eventually the front pair breaks away and leaves behind the other two bubbles.

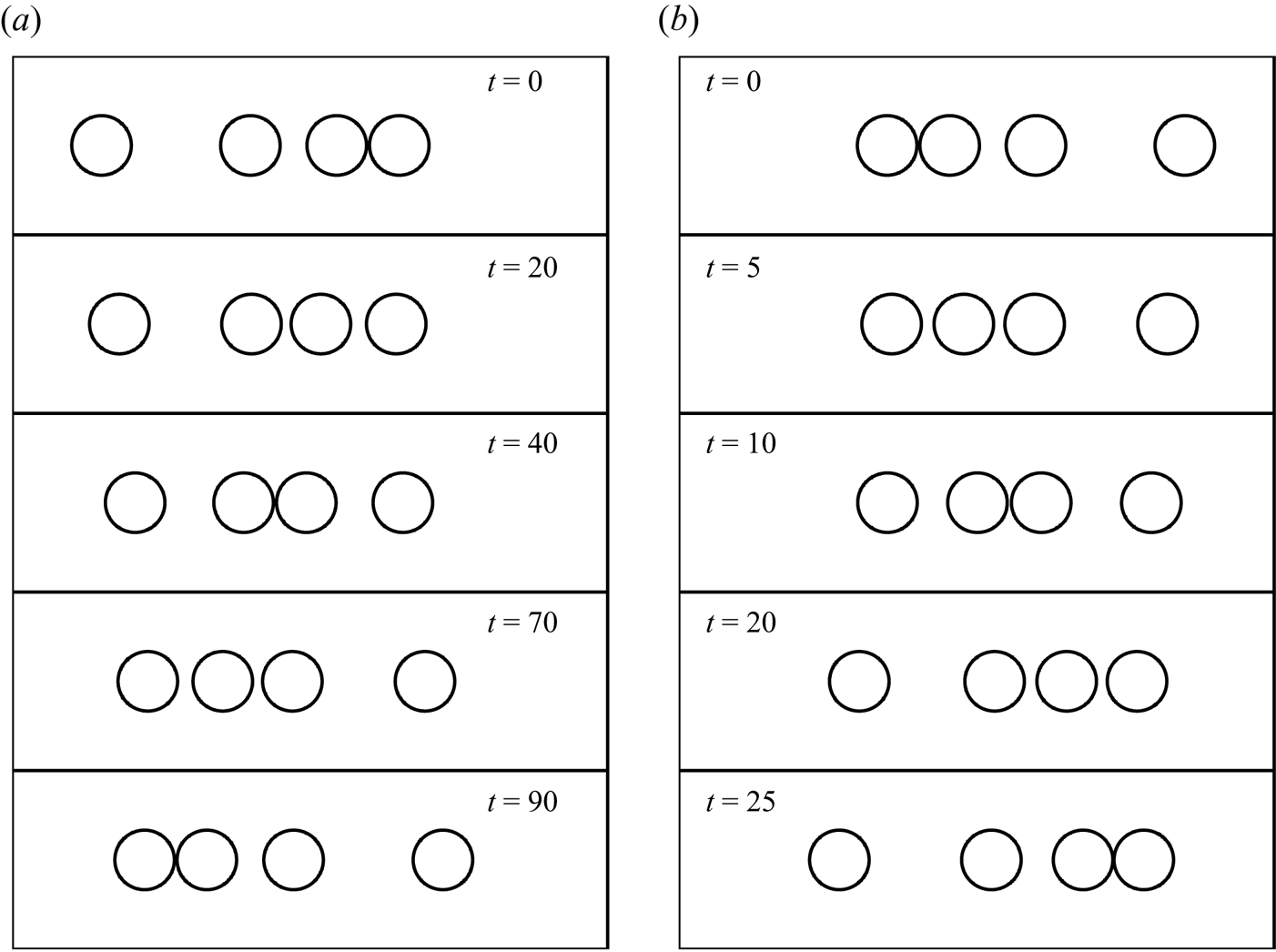
Figure 9. The progression of a series of four identical bubbles, with (a) $\delta =1/2$, (b) $\delta =5$.

The formation and breakup of successive bubble pairs observed in figure 9 is highly reminiscent of a Newton's cradle, even though there is no inertia in our system, and the motion arises solely due to viscous hydrodynamic interactions.