Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-16T18:25:41.316Z Has data issue: false hasContentIssue false
  • English
  • Français

Barotropic theory for the velocity profile of Jupiter’s turbulent jets: an example for an exact turbulent closure

Published online by Cambridge University Press:  07 December 2018

E. Woillez Open the ORCID record for E. Woillez [Opens in a new window]  and
F. Bouchet
E. Woillez
Affiliation:
Université de Lyon, ENS de Lyon, Université Claude Bernard, CNRS, Laboratoire de Physique, F-69342 Lyon, France
F. Bouchet*
Affiliation:
Université de Lyon, ENS de Lyon, Université Claude Bernard, CNRS, Laboratoire de Physique, F-69342 Lyon, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We model the dynamics of Jupiter’s jets by the stochastic barotropic 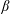$\unicode[STIX]{x1D6FD}$-plane model. In this simple framework, by analytic computation of the averaged effect of eddies, we obtain three new explicit results about the equilibrium structure of jets. First we obtain a very simple explicit relation between the Reynolds stresses, the energy injection rate and the averaged velocity shear. This predicts the averaged velocity profile far from the jet edges (extrema of zonal velocity). Our approach takes advantage of a time-scale separation between the inertial dynamics on one hand, and the spin-up (or spin-down) time on the other. Second, a specific asymptotic expansion close to the eastward jet extremum explains the formation of a cusp at the scale of energy injection, characterized by a curvature that is independent of the forcing spectrum. Finally, we derive equations that describe the evolution of the westward tip of the jets. The analysis of these equations is consistent with the previously discussed picture of barotropic adjustment, explaining the relation between the westward jet curvature and the 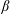$\unicode[STIX]{x1D6FD}$-effect. Our results give a consistent overall theory of the stationary velocity profile of inertial barotropic zonal jets, in the limit of small-scale forcing.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Geophysical and Geological Flows: Geostrophic turbulence Turbulent Flows: Turbulence theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 860 , 10 February 2019 , pp. 577 - 607
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bakas, N. & Ioannou, P. 2014 A theory for the emergence of coherent structures in beta-plane turbulence. J. Fluid Mech. 740, 312–340.Google Scholar
Bouchet, F. & Morita, H. 2010 Large time behavior and asymptotic stability of the 2D Euler and linearized Euler equations. Physica D 239, 948–966.Google Scholar
Bouchet, F., Nardini, C. & Tangarife, T. 2013 Kinetic theory of jet dynamics in the stochastic barotropic and 2D Navier–Stokes equations. J. Stat. Phys. 153 (4), 572–625.Google Scholar
Bouchet, F., Nardini, C. & Tangarife, T. 2016 Kinetic theory and quasilinear theories of jet dynamics. In Zonal Flows (ed. Galperin, B.), Cambridge University Press.Google Scholar
Bouchet, F. & Simonnet, E. 2009 Random changes of flow topology in two-dimensional and geophysical turbulence. Phys. Rev. Lett. 102 (9), 094504.Google Scholar
Bouchet, F. & Venaille, A. 2012 Statistical mechanics of two-dimensional and geophysical flows. Phys. Rep. 515, 227–295.Google Scholar
Brunet, G. 1990 Dynamique des Ondes de Rossby dans un Jet Parabolique. Université McGill.Google Scholar
Constantinou, N. C.2015 Formation of large-scale structures by turbulence in rotating planets. Preprint, arXiv:1503.07644.Google Scholar
Constantinou, N. C., Farrell, B. F. & Ioannou, P. J. 2014 Emergence and equilibration of jets in beta-plane turbulence: applications of stochastic structural stability theory. J. Atmos. Sci. 71 (5), 1818–1842.Google Scholar
Drazin, P. G., Beaumont, D. N. & Coaker, S. A. 1982 On Rossby waves modified by basic shear, and barotropic instability. J. Fluid Mech. 124, 439–456.Google Scholar
Drazin, P. G. & Reid, W. H. 2004 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Dritschel, D. G. & McIntyre, M. E. 2008 Multiple jets as PV staircases: the Phillips effect and the resilience of eddy-transport barriers. J. Atmos. Sci. 65, 855–874.Google Scholar
Farrell, B. F. & Ioannou, P. J. 2003 Structural stability of turbulent jets. J. Atmos. Sci. 60, 2101–2118.Google Scholar
Farrell, B. F. & Ioannou, P. J. 2007 Structure and spacing of jets in barotropic turbulence. J. Atmos. Sci. 64, 3652–3665.Google Scholar
Frishman, A., Laurie, J. & Falkovich, G. 2017 Jets or vortices? What flows are generated by an inverse turbulent cascade? Phys. Rev. Fluids 2 (3), 032602.Google Scholar
Galperin, B., Sukoriansky, S. & Huang, H.-P. 2001 Universal n -5 spectrum of zonal flows on giant planets. Phys. Fluids 13 (6), 1545–1548.Google Scholar
Galperin, B., Young, R. M., Sukoriansky, S., Dikovskaya, N., Read, P. L., Lancaster, A. J. & Armstrong, D. 2014 Cassini observations reveal a regime of zonostrophic macroturbulence on Jupiter. Icarus 229, 295–320.Google Scholar
Garcí, E. & Sánchez-Lavega, A. 2001 A study of the stability of jovian zonal winds from HST images: 1995–2000. Icarus 152 (2), 316–330.Google Scholar
Ingersoll, A. P. 1990 Atmospheric dynamics of the outer planets. Science 248 (4953), 308–315.Google Scholar
Ingersoll, A. P., Beebe, R. F., Mitchell, J. L., Garneau, G. W., Yagi, G. M. & Müller, J.-P. 1981 Interaction of eddies and mean zonal flow on Jupiter as inferred from Voyager 1 and 2 images. J. Geophys. Res. A 86 (A10), 8733–8743.Google Scholar
Kolokolov, I. V. & Lebedev, V. V. 2016a Structure of coherent vortices generated by the inverse cascade of two-dimensional turbulence in a finite box. Phys. Rev. E 93 (3), 033104.Google Scholar
Kolokolov, I. V. & Lebedev, V. V. 2016b Velocity statistics inside coherent vortices generated by the inverse cascade of 2-D turbulence. J. Fluid Mech. 809, R2.Google Scholar
Laurie, J., Boffetta, G., Falkovich, G., Kolokolov, I. & Lebedev, V. 2014 Universal profile of the vortex condensate in two-dimensional turbulence. Phys. Rev. Lett. 113 (25), 254503.Google Scholar
Li, L., Ingersoll, A. P. & Huang, X. 2006 Interaction of moist convection with zonal jets on Jupiter and Saturn. Icarus 180 (1), 113–123.Google Scholar
Marston, J. B., Conover, E. & Schneider, T. 2008 Statistics of an unstable barotropic jet from a cumulant expansion. J. Atmos. Sci. 65, 1955–1966.Google Scholar
Pedlosky, J. 1964 The stability of currents in the atmosphere and the ocean: Part II. J. Atmos. Sci. 21 (4), 342–353.Google Scholar
Pedlosky, J. 1982 Geophysical Fluid Dynamics. Springer.Google Scholar
Porco, C. C., West, R. A., McEwen, A., Del Genio, A. D., Ingersoll, A. P., Thomas, P., Squyres, S., Dones, L., Murray, C. D., Johnson, T. V. et al. 2003 Cassini imaging of Jupiter’s atmosphere, satellites, and rings. Science 299 (5612), 1541–1547.Google Scholar
Read, P. L., Yamazaki, Y. H., Lewis, S. R., Williams, P. D., Miki-Yamazaki, K., Sommeria, J., Didelle, H. & Fincham, A. 2004 Jupiter’s and Saturn’s convectively driven banded jets in the laboratory. Geophys. Res. Lett. 31 (22), L22701.Google Scholar
Reed, M. & Simon, B. 1978 Modern methods of mathematical physics. In Analysis of Operators. Academic Press.Google Scholar
Salyk, C., Ingersoll, A. P., Lorre, J., Vasavada, A. & Del Genio, A. D. 2006 Interaction between eddies and mean flow in Jupiter’s atmosphere: analysis of Cassini imaging data. Icarus 185 (2), 430–442.Google Scholar
Sánchez-Lavega, A., Orton, G. S., Hueso, R., García-Melendo, E., Pérez-Hoyos, S., Simon-Miller, A., Rojas, J. F., Gómez, J. M., Yanamandra-Fisher, P., Fletcher, L. et al. 2008 Depth of a strong jovian jet from a planetary-scale disturbance driven by storms. Nature 451 (7177), 437–440.Google Scholar
Schneider, T. & Liu, J. 2009 Formation of jets and equatorial superrotation on Jupiter. J. Atmos. Sci. 66, 579–601.Google Scholar
Sommeria, J. 1986 Experimental study of the two-dimensional inverse energy cascade in a square box. J. Fluid Mech. 170, 139–168.Google Scholar
Srinivasan, K. & Young, W. R. 2014 Reynolds stress and eddy diffusivity of 𝛽-plane shear flows. J. Atmos. Sci. 71 (6), 2169–2185.Google Scholar
Vallis, G. K. & Maltrud, M. E. 1993 Generation of mean flows and jets on a beta plane and over topography. J. Phys. Oceanogr. 23 (7), 1346–1362.Google Scholar
Vasavada, A. R. & Showman, A. P. 2005 Jovian atmospheric dynamics: an update after Galileo and Cassini. Rep. Progr. Phys. 68 (8), 1935.Google Scholar
Williams, G. P. 1978 Planetary circulations: 1. Barotropic representation of Jovian and terrestrial turbulence. J. Atmos. Sci. 35 (8), 1399–1426.Google Scholar
Woillez, E. & Bouchet, F. 2017 Theoretical prediction of Reynolds stresses and velocity profiles for barotropic turbulent jets. Europhys. Lett. 118 (5), 54002.Google Scholar