Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-23T03:28:40.977Z Has data issue: false hasContentIssue false
  • English
  • Français

An elaborate experiment on the single-mode Richtmyer–Meshkov instability

Published online by Cambridge University Press:  23 August 2018

Lili Liu ,
Yu Liang ,
Juchun Ding ,
Naian Liu  and
Xisheng Luo Open the ORCID record for Xisheng Luo [Opens in a new window]
Lili Liu
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China
Yu Liang
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China
Juchun Ding
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China
Naian Liu
Affiliation:
State Key Laboratory of Fire Science, University of Science and Technology of China, Hefei 230026, China
Xisheng Luo*
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China State Key Laboratory of Fire Science, University of Science and Technology of China, Hefei 230026, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

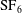High-fidelity experiments of Richtmyer–Meshkov instability on a single-mode air/$\text{SF}_{6}$ interface are carried out at weak shock conditions. The soap-film technique is extended to create single-mode gaseous interfaces which are free of small-wavelength perturbations, diffusion layers and three-dimensionality. The interfacial morphologies captured show that the instability evolution evidently involves the smallest experimental uncertainty among all existing results. The performances of the impulsive model and other nonlinear models are thoroughly examined through temporal variations of the perturbation amplitude. The individual growth of bubbles or spikes demonstrates that all nonlinear models can provide a reliable forecast of bubble development, but only the model of Zhang & Guo (J. Fluid Mech., vol. 786, 2016, pp. 47–61) can reasonably predict spike development. The distinct images of the interface morphology obtained also provide a rare opportunity to extract interface contours such that a spectral analysis of the interfacial contours can be performed, which realizes the first direct validation of the high-order nonlinear models of Zhang & Sohn (Phys. Fluids, vol. 9, 1997, pp. 1106–1124) and Vandenboomgaerde et al. (Phys. Fluids, vol. 14 (3), 2002, pp. 1111–1122) in terms of the fundamental mode and high-order harmonics. It is found that both models show a very good and almost identical accuracy in predicting the first two modes. However, the model of Zhang & Sohn (1997) becomes much more accurate in modelling the third-order harmonics due to the fewer simplifications used.

JFM classification

Instability: Nonlinear instability Compressible Flows: Shock waves Mixing: Turbulent mixing
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 853 , 25 October 2018 , R2
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arnett, W. D., Bahcall, J. N., Kirshner, R. P. & Woosley, S. E. 1989 Supernova 1987A. Annu. Rev. Astron. Astrophys. 27, 629–700.Google Scholar
Balakumar, B. J., Orlicz, G. C., Ristorcelli, J. R., Balasubramanian, S., Prestridge, K. P. & Tomkins, C. D. 2012 Turbulent mixing in a Richtmyer–Meshkov fluid layer after reshock: velocity and density statistics. J. Fluid Mech. 696, 67–93.Google Scholar
Brouillette, M. 2002 The Richtmyer–Meshkov instability. Annu. Rev. Fluid Mech. 34, 445–468.Google Scholar
Brouillette, M. & Bonazza, R. 1999 Experiments on the Richtmyer–Meshkov instability: wall effects and wave phenomena. Phys. Fluids 11, 1127–1142.Google Scholar
Collins, B. D. & Jacobs, J. W. 2002 PLIF flow visualization and measurements of the Richtmyer–Meshkov instability of an air/SF6 interface. J. Fluid Mech. 464, 113–136.Google Scholar
Dimonte, G. & Ramaprabhu, P. 2010 Simulations and model of the nonlinear Richtmyer–Meshkov instability. Phys. Fluids 22, 014104.Google Scholar
Ding, J., Si, T., Chen, M., Zhai, Z., Lu, X. & Luo, X. 2017 On the interaction of a planar shock with a three-dimensional light gas cylinder. J. Fluid Mech. 828, 289–317.Google Scholar
Erez, L., Sadot, O., Oron, D., Erez, G., Levin, L. A., Shvarts, D. & Ben-Dor, G. 2000 Study of membrane effect on turbulent mixing measurements in shock tubes. Shock Waves 10, 241–251.Google Scholar
Fontaine, G., Mariani, C., Martinez, S., Jourdan, G., Houas, L., Vandenboomgaerde, M. & Souffland, D. 2009 An attempt to reduce the membrane effects in Richtmyer–Meshkov instability shock tube experiments. Shock Waves 19, 285–289.Google Scholar
Goncharov, V. N. 2002 Analytical model of nonlinear, single-mode, classical Rayleigh–Taylor instability at arbitrary Atwood numbers. Phys. Rev. Lett. 88, 134502.Google Scholar
Haas, J. F. & Sturtevant, B. 1987 Interaction of weak shock waves with cylindrical and spherical gas inhomogeneities. J. Fluid Mech. 181, 41–76.Google Scholar
Jacobs, J. W. & Krivets, V. V. 2005 Experiments on the late-time development of single-mode Richtmyer–Meshkov instability. Phys. Fluids 17, 034105.Google Scholar
Jones, M. A. & Jacobs, J. W. 1997 A membraneless experiment for the study of Richtmyer–Meshkov instability of a shock-accelerated gas interface. Phys. Fluids 9, 3078–3085.Google Scholar
Jourdan, G. & Houas, L. 2005 High-amplitude single-mode perturbation evolution at the Richtmyer–Meshkov instability. Phys. Rev. Lett. 95, 204502.Google Scholar
Layes, G., Jourdan, G. & Houas, L. 2009 Experimental study on a plane shock wave accelerating a gas bubble. Phys. Fluids 21, 074102.Google Scholar
Lindl, J., Landen, O., Edwards, J., Moses, E. & Team, N. 2014 Review of the National Ignition Campaign 2009–2012. Phys. Plasmas 21, 020501.Google Scholar
Lombardini, M. & Pullin, D. I. 2009 Startup process in the Richtmyer–Meshkov instability. Phys. Fluids 21 (4), 044104.Google Scholar
Luo, X., Wang, X. & Si, T. 2013 The Richtmyer–Meshkov instability of a three-dimensional air/SF6 interface with a minimum-surface feature. J. Fluid Mech. 722, R2.Google Scholar
Luo, X., Zhai, Z., Si, T. & Yang, J. 2014 Experimental study on the interfacial instability induced by shock waves. Adv. Mech. 44, 260–290.Google Scholar
Mariani, C., Vandenboomgaerde, M., Jourdan, G., Souffland, D. & Houas, L. 2008 Investigation of the Richtmyer–Meshkov instability with stereolithographed interfaces. Phys. Rev. Lett. 100, 254503.Google Scholar
Meshkov, E. E. 1969 Instability of the interface of two gases accelerated by a shock wave. Fluid Dyn. 4, 101–104.Google Scholar
Meyer, K. A. & Blewett, P. J. 1972 Numerical investigation of the stability of a shock-accelerated interface between two fluids. Phys. Fluids 15, 753–759.Google Scholar
Mikaelian, K. O. 2003 Explicit expressions for the evolution of single-mode Rayleigh–Taylor and Richtmyer–Meshkov instabilities at arbitrary Atwood numbers. Phys. Rev. E 67, 026319.Google Scholar
Mikaelian, K. O. 2008 Limitations and failures of the Layzer model for hydrodynamic instabilities. Phys. Rev. E 78, 015303.Google Scholar
Ranjan, D., Oakley, J. & Bonazza, R. 2011 Shock-bubble interactions. Annu. Rev. Fluid Mech. 43, 117–140.Google Scholar
Richtmyer, R. D. 1960 Taylor instability in shock acceleration of compressible fluids. Commun. Pure Appl. Maths 13, 297–319.Google Scholar
Sadot, O., Erez, L., Alon, U., Oron, D., Levin, L. A., Erez, G., Ben-Dor, G. & Shvarts, D. 1998 Study of nonlinear evolution of single-mode and two-bubble interaction under Richtmyer–Meshkov instability. Phys. Rev. Lett. 80, 1654–1657.Google Scholar
Sohn, S. I. 2003 Simple potential-flow model of Rayleigh–Taylor and Richtmyer–Meshkov instabilities for all density ratios. Phys. Rev. E 67, 026301.Google Scholar
Vandenboomgaerde, M., Gauthier, S. & Mügler, C. 2002 Nonlinear regime of a multimode Richtmyer–Meshkov instability: a simplified perturbation theory. Phys. Fluids 14 (3), 1111–1122.Google Scholar
Vandenboomgaerde, M., Souffland, D., Mariani, C., Biamino, L., Jourdan, G. & Houas, L. 2014 An experimental and numerical investigation of the dependency on the initial conditions of the Richtmyer–Meshkov instability. Phys. Fluids 26 (2), 024109.Google Scholar
Weber, C., Haehn, N., Oakley, J., Rothamer, D. & Bonazza, R. 2012 Turbulent mixing measurements in the Richtmyer–Meshkov instability. Phys. Fluids 24, 074105.Google Scholar
Wouchuk, J. G. 2001 Growth rate of the linear Richtmyer–Meshkov instability when a shock is reflected. Phys. Rev. E 63, 056303.Google Scholar
Yang, J., Kubota, T. & Zukoski, E. E. 1993 Application of shock-induced mixing to supersonic combustion. AIAA J. 31, 854–862.Google Scholar
Zabusky, N. J. 1999 Vortex paradigm for accelerated inhomogeneous flows: visiometrics for the Rayleigh–Taylor and Richtmyer–Meshkov environments. Annu. Rev. Fluid Mech. 31, 495–536.Google Scholar
Zhai, Z., Si, T., Luo, X. & Yang, J. 2011 On the evolution of spherical gas interfaces accelerated by a planar shock wave. Phys. Fluids 23, 084104.Google Scholar
Zhang, Q. & Guo, W. 2016 Universality of finger growth in two-dimensional Rayleigh–Taylor and Richtmyer–Meshkov instabilities with all density ratios. J. Fluid Mech. 786, 47–61.Google Scholar
Zhang, Q. & Sohn, S. I. 1996 An analytical nonlinear theory of Richtmyer–Meshkov instability. Phys. Lett. A 212, 149–155.Google Scholar
Zhang, Q. & Sohn, S. I. 1997 Nonlinear theory of unstable fluid mixing driven by shock wave. Phys. Fluids 9, 1106–1124.Google Scholar
Zhang, Q. & Sohn, S. I. 1999 Quantitative theory of Richtmyer–Meshkov instability in three dimensions. Z. Angew. Math. Phys. 50, 1–46.Google Scholar