Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T00:58:36.910Z Has data issue: false hasContentIssue false
  • English
  • Français

Wake dynamics and flow-induced vibration of a freely rolling cylinder

Published online by Cambridge University Press:  02 October 2020

F. Y. Houdroge Open the ORCID record for F. Y. Houdroge [Opens in a new window] ,
T. Leweke Open the ORCID record for T. Leweke [Opens in a new window] ,
K. Hourigan  and
M. C. Thompson
F. Y. Houdroge
Affiliation:
FLAIR, Department of Mechanical and Aerospace Engineering, Monash University, Clayton, VIC3800, Australia
T. Leweke
Affiliation:
IRPHE, CNRS, Aix-Marseille Université, Centrale Marseille, 13384Marseille, France
K. Hourigan
Affiliation:
FLAIR, Department of Mechanical and Aerospace Engineering, Monash University, Clayton, VIC3800, Australia
M. C. Thompson*
Affiliation:
FLAIR, Department of Mechanical and Aerospace Engineering, Monash University, Clayton, VIC3800, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

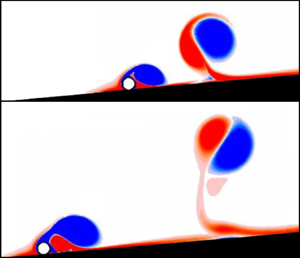
This article examines numerically the two-dimensional fluid–structure interaction problem of a circular cylinder rolling under gravity along an inclined surface under the assumption of a fixed but small gap. The motion of the cylinder is governed by the ratio of cylinder and fluid densities and the Reynolds number based on a velocity scale derived from the momentum balance in the asymptotic regime. For increasing Reynolds number, the cylinder wake undergoes a transition from steady to periodic flow, causing oscillations of the cylinder motion. The critical Reynolds number increases for light cylinders. Whereas the time-averaged characteristics of the asymptotic rolling states depend only on the Reynolds number, the density ratio has an additional influence on the vibration amplitude and on the cylinder motion during a start-up transient from rest. Light cylinders reach their final state quickly after the initial acceleration; heavier cylinders traverse a series of quasi-steady states, including a temporary velocity overshoot, before settling in the asymptotic regime. The amplitudes of the flow-induced vibrations remain small over the entire parameter range, which can be attributed to the value of the added-mass force associated with a rolling cylinder. Special attention is paid to the influence of the small but finite gap between cylinder and wall, since lubrication theory predicts a diverging pressure drag for a vanishing gap. The variations with gap size of the forces, torque and added mass are explored. The gap also influences the characteristics of the cylinder vibrations in the unsteady wake regime, in particular their amplitude.

JFM classification

Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 903 , 25 November 2020 , A48
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Anagnostopoulos, P. & Bearman, P. W. 1992 Response characteristics of a vortex-excited cylinder at low Reynolds numbers. J. Fluids Struct. 6, 39–50.Google Scholar
Armaly, B. F., Durst, F., Pereira, J. C. F. & Schönung, B. 1983 Experimental and theoretical investigation of backward-facing step flow. J. Fluid Mech. 127, 473–496.Google Scholar
Barkley, D. & Henderson, R. D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.Google Scholar
Blackburn, H. M. & Henderson, R. 1996 Lock-in behavior in simulated vortex-induced vibration. Exp. Therm. Fluid Sci. 12, 184–189.Google Scholar
Blackburn, H. M. & Karniadakis, G. E. 1993 Two- and three-dimensional simulations of vortex-induced vibration of a circular cylinder. In Third International Offshore and Polar Engineering Conference (ed. Chung, J. S., Natvig, B. J., Das, B. M. & Li, Y.-C.), pp. 715–720.Google Scholar
Bourguet, R. & Lo Jacono, D. 2014 Flow-induced vibrations of a rotating cylinder. J. Fluid Mech. 740, 342–380.Google Scholar
Brennan, C. E. 1982 A review of added mass and fluid inertial forces. Tech. Rep. N62583-81-MR-554. Naval Civil Engineering Laboratory.Google Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. & Zang, T. A. 2007 Spectral Methods. Springer.CrossRefGoogle Scholar
Carty, J. J. 1957 Resistance coefficients for spheres on a plane boundary. BSc thesis, Massachusetts Institute of Technology, Cambridge, MA.Google Scholar
Chhabra, R. P. & Ferreira, J. M. 1999 An analytical study of the motion of a sphere rolling down a smooth inclined plane in an incompressible Newtonian fluid. Powder Technol. 104, 130–138.Google Scholar
Chung, H. & Chen, S. S. 1984 Hydrodynamic mass. Internal Report CONF-840647–9, Argonne National Laboratory.Google Scholar
Feng, C. C. 1968 The measurement of vortex induced effects in flow past stationary and oscillating circular and D-section cylinders. PhD thesis, University of British Columbia.Google Scholar
Fredsøe, J., Sumer, B. M., Andersen, J. & Hansen, E. A. 1987 Transverse vibrations of a cylinder very close to a plane wall. Trans. ASME: J. Offshore Mech. Arctic Engng 109, 52–60.Google Scholar
Govardhan, R. & Williamson, C. H. K. 2000 Modes of vortex formation and frequency response of a freely vibrating cylinder. J. Fluid Mech. 420, 85–130.CrossRefGoogle Scholar
Guilmineau, E. & Queutey, P. 2002 A numerical simulation of vortex shedding from an oscillating circular cylinder. J. Fluids Struct. 16, 773–794.CrossRefGoogle Scholar
Henderson, R. D. 1997 Nonlinear dynamics and pattern formation in turbulent wake transition. J. Fluid Mech. 352, 65–112.CrossRefGoogle Scholar
Houdroge, F. Y., Leweke, T., Hourigan, K. & Thompson, M. C. 2017 Two- and three-dimensional wake transitions of an impulsively started uniformly rolling circular cylinder. J. Fluid Mech. 826, 32–59.CrossRefGoogle Scholar
Jan, C.-D. & Chen, J.-C. 1997 Movements of a sphere rolling down an inclined plane. J. Hydraul. Res. 35, 689–706.CrossRefGoogle Scholar
Jeffrey, D. J. & Onishi, Y. 1981 The slow motion of a cylinder next to a plane wall. Q. J. Mech. Appl. Maths 34, 129–137.CrossRefGoogle Scholar
Karniadakis, G. Em. & Sherwin, S. J. 1999 Spectral/hp Element Methods for Computational Fluid Dynamics. Oxford University Press.Google Scholar
Khalak, A. & Williamson, C. H. K. 1996 Dynamics of a hydroelastic cylinder with very low mass and damping. J. Fluids Struct. 10, 455–472.CrossRefGoogle Scholar
Khalak, A. & Williamson, C. H. K. 1999 Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping. J. Fluids Struct. 13, 813–851.CrossRefGoogle Scholar
Lee, H., Hourigan, K. & Thompson, M. C. 2013 Vortex-induced vibration of a neutrally buoyant tethered sphere. J. Fluid Mech. 719, 97–128.CrossRefGoogle Scholar
Lei, C., Cheng, L. & Kavanagh, K. 1999 Re-examination of the effect of a plane boundary on force and vortex shedding of a circular cylinder. J. Wind Engng Ind. Aerodyn. 80, 263–286.CrossRefGoogle Scholar
Leontini, J. S., Thompson, M. C. & Hourigan, K. 2006 The beginning of branching behaviour of vortex-induced vibration during two-dimensional flow. J. Fluids Struct. 22, 857–864.CrossRefGoogle Scholar
Leontini, J. S., Thompson, M. C. & Hourigan, K. 2007 Three-dimensional transition in the wake of a transversely oscillating cylinder. J. Fluid Mech. 577, 79–104.CrossRefGoogle Scholar
Li, Z., Yao, W., Yang, K., Jaiman, R. K. & Khoo, B. C. 2016 On the vortex-induced oscillations of a freely vibrating cylinder in the vicinity of a stationary plane wall. J. Fluids Struct. 65, 495–526.CrossRefGoogle Scholar
Lighthill, J. 1986 Wave loading on offshore structures. J. Fluid Mech. 173, 667–681.CrossRefGoogle Scholar
Magnus, G. 1853 Ueber die Abweichung der Geschosse, und: Ueber eine auffallende Erscheinung bei rotirenden Körpern. Ann. Phys. Chem. 164, 1–29.CrossRefGoogle Scholar
Merlen, A. & Frankiewicz, C. 2011 Cylinder rolling on a wall at low Reynolds numbers. J. Fluid Mech. 685, 461–494.CrossRefGoogle Scholar
Mittal, S. & Kumar, B. 2003 Flow past a rotating cylinder. J. Fluid Mech. 476, 303–334.CrossRefGoogle Scholar
Mittal, S. & Singh, S. 2005 Vortex-induced vibrations at subcritical Re. J. Fluid Mech. 534, 185–194.CrossRefGoogle Scholar
Mysa, C. R., Kaboudian, A. & Jaiman, R. K. 2016 On the origin of wake-induced vibration in two tandem circular cylinders at low Reynolds number. J. Fluids Struct. 61, 76–98.CrossRefGoogle Scholar
Prasanth, T. K. & Mittal, S. 2008 Vortex-induced vibrations of a circular cylinder at low Reynolds numbers. J. Fluid Mech. 594, 463–491.CrossRefGoogle Scholar
Prasanth, T. K. & Mittal, S. 2009 Vortex-induced vibration of two circular cylinders at low Reynolds number. J. Fluids Struct. 25, 731–741.CrossRefGoogle Scholar
Prokunin, A. N. 2003 On a paradox in the motion of a rigid particle along a wall in a fluid. Fluid Dyn. 38, 443–457.CrossRefGoogle Scholar
Provansal, M., Mathis, C. & Boyer, L. 1987 Bénard-von Kármán instability: transient and forced regimes. J. Fluid Mech. 182, 1–22.CrossRefGoogle Scholar
Radi, A., Thompson, M. C., Rao, A., Hourigan, K. & Sheridan, J. 2013 Experimental evidence of new three-dimensional modes in the wake of a rotating cylinder. J. Fluid Mech. 734, 567–594.CrossRefGoogle Scholar
Raghavan, K., Bernitsas, M. M. & Maroulis, D. E. 2009 Effect of bottom boundary on VIV for energy harnessing at $8\times 10^3 < Re < 1.5\times 10^5$. Trans. ASME: J. Offshore Mech. Arctic Engng 131, 031102.Google Scholar
Rajamuni, M. M., Thompson, M. C. & Hourigan, K. 2020 Vortex dynamics and vibration modes of a tethered sphere. J. Fluid Mech. 885, A10.CrossRefGoogle Scholar
Rao, A., Leontini, J., Thompson, M. C. & Hourigan, K. 2013 a Three-dimensionality in the wake of a rotating cylinder in a uniform flow. J. Fluid Mech. 717, 1–29.CrossRefGoogle Scholar
Rao, A., Leontini, J. S., Thompson, M. C. & Hourigan, K. 2013 b Three-dimensionality in the wake of a rapidly rotating cylinder in uniform flow. J. Fluid Mech. 730, 379–391.CrossRefGoogle Scholar
Rao, A., Stewart, B. E., Thompson, M. C., Leweke, T. & Hourigan, K. 2011 Flows past rotating cylinders next to a wall. J. Fluids Struct. 27, 668–679.CrossRefGoogle Scholar
Rao, A., Thompson, M. C., Leweke, T. & Hourigan, K. 2013 c The flow past a circular cylinder translating at different heights above a wall. J. Fluids Struct. 41, 9–21.CrossRefGoogle Scholar
Rao, A., Thompson, M. C., Leweke, T. & Hourigan, K. 2015 Flow past a rotating cylinder translating at different gap heights along a wall. J. Fluids Struct. 57, 314–330.CrossRefGoogle Scholar
Roshko, A. 1954 On the development of turbulent wakes from vortex streets. NACA Tech. Rep. 1191.Google Scholar
Ryan, K., Thompson, M. C. & Hourigan, K. 2005 Three-dimensional transition in the wake of bluff elongated cylinders. J. Fluid Mech. 538, 1–29.CrossRefGoogle Scholar
Ryan, K., Thompson, M. C. & Hourigan, K. 2007 The effect of mass ratio and tether length on the flow around a tethered cylinder. J. Fluid Mech. 591, 117–144.CrossRefGoogle Scholar
Sarpkaya, T. 1979 Vortex-induced oscillations: a selective review. J. Appl. Mech. 46, 241–258.CrossRefGoogle Scholar
Seddon, J. R. T. & Mullin, T. 2006 Reverse rotation of a cylinder near a wall. Phys. Fluids 18, 041703.CrossRefGoogle Scholar
Shiels, D., Leonard, A. & Roshko, A. 2001 Flow-induced vibration of a circular cylinder at limiting structural parameters. J. Fluids Struct. 15, 3–21.CrossRefGoogle Scholar
Stewart, B. E., Hourigan, K., Thompson, M. C. & Leweke, T. 2006 Flow dynamics and forces associated with a cylinder rolling along a wall. Phys. Fluids 18, 111701.CrossRefGoogle Scholar
Stewart, B. E., Thompson, M. C., Leweke, T. & Hourigan, K. 2010 a Numerical and experimental studies of the rolling sphere wake. J. Fluid Mech. 643, 137–162.CrossRefGoogle Scholar
Stewart, B. E., Thompson, M. C., Leweke, T. & Hourigan, K. 2010 b The wake behind a cylinder rolling on a wall at varying rotation rates. J. Fluid Mech. 648, 225–256.CrossRefGoogle Scholar
Taneda, S. 1956 Experimental investigation of the wakes behind cylinders and plates at low Reynolds numbers. J. Phys. Soc. Japan 11, 1104–1108.CrossRefGoogle Scholar
Taneda, S. 1965 Experimental investigation of vortex streets. J. Phys. Soc. Japan 20, 1714–1721.CrossRefGoogle Scholar
Tang, T. & Ingham, D. B. 1991 On steady flow past a rotating circular cylinder at Reynolds numbers 60 and 100. Comput. Fluids 19, 217–230.CrossRefGoogle Scholar
Tham, D. M. Y, Gurugubelli, P. S., Li, Z. & Jaiman, R. K. 2015 Freely vibrating circular cylinder in the vicinity of a stationary wall. J. Fluids Struct. 59, 103–128.CrossRefGoogle Scholar
Thompson, M. C., Hourigan, K., Cheung, A. & Leweke, T. 2006 Hydrodynamics of a particle impact on a wall. Appl. Math. Model. 30, 1356–1369.CrossRefGoogle Scholar
Thompson, M. C., Hourigan, K. & Sheridan, J. 1996 Three-dimensional instabilities in the wake of a circular cylinder. Exp. Therm. Fluid Sci. 12, 190–196.CrossRefGoogle Scholar
Thompson, M. C., Leweke, T. & Williamson, C. H. K. 2001 The physical mechanism of transition in bluff body wakes. J. Fluids Struct. 15, 607–616.CrossRefGoogle Scholar
Tsahalis, D. T. 1983 The effect of seabottom proximity of the vortex-induced vibrations and fatigue life of offshore pipelines. J. Energy Resour. Technol. 105, 464–468.CrossRefGoogle Scholar
Wang, X. K., Hao, Z. & Tan, S. K. 2013 Vortex-induced vibrations of a neutrally buoyant circular cylinder near a plane wall. J. Fluids Struct. 39, 188–204.CrossRefGoogle Scholar
Williamson, C. H. K. 1988 The existence of two stages in the transition to three-dimensionality of a cylinder wake. Phys. Fluids 31, 3165–3168.CrossRefGoogle Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.CrossRefGoogle Scholar
Williamson, C. H. K. & Govardhan, R. 2004 Vortex-induced vibrations. Annu. Rev. Fluid Mech. 36, 413–455.CrossRefGoogle Scholar
Williamson, C. H. K. & Roshko, A. 1988 Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 2, 355–381.CrossRefGoogle Scholar
Wong, K. W., Zhao, J., Lo Jacono, D., Thompson, M. C. & Sheridan, J. 2017 Experimental investigation of flow-induced vibration of a rotating circular cylinder. J. Fluid Mech. 829, 486–511.CrossRefGoogle Scholar
Yang, B., Gao, F., Jeng, D. S. & Wu, Y. 2009 Experimental study of vortex-induced vibrations of a cylinder near a rigid plane boundary in steady flow. Acta Mechanica Sin. 25, 51–63.CrossRefGoogle Scholar
Yang, B., Gao, F. & Wu, Y. 2008 Experimental study on flow induced vibration of a cylinder with two degrees of freedom near a rigid wall. In The Eighteenth International Offshore and Polar Engineering Conference (ed. Chung, J. S., Hong, S. W., Prinsenberg, S. & Nagata, S.), vol. 3, pp. 469–473.Google Scholar
Zdravkovich, M. M. 1985 Observation of vortex shedding behind a towed circular cylinder near a wall. In Flow Visualization III (ed. Yang, W. J.), pp. 423–427.Google Scholar
Zhang, C., Soga, K., Kumar, K., Sun, Q. & Jin, F. 2017 Numerical study of a sphere descending along an inclined slope in a liquid. Granul. Matter 19, 85.CrossRefGoogle Scholar
Zhao, M. & Cheng, L. 2011 Numerical simulation of two-degree-of-freedom vortex-induced vibration of a circular cylinder close to a plane boundary. J. Fluids Struct. 27, 1097–1110.CrossRefGoogle Scholar
Zhao, M., Cheng, L. & Lu, L. 2014 Vortex induced vibrations of a rotating circular cylinder at low Reynolds number. Phys. Fluids 26, 073602.CrossRefGoogle Scholar