Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-19T10:08:25.421Z Has data issue: false hasContentIssue false
  • English
  • Français

Very near-nozzle shear-layer turbulence and jet noise

Published online by Cambridge University Press:  27 March 2015

Ryan A. Fontaine ,
Gregory S. Elliott ,
Joanna M. Austin  and
Jonathan B. Freund
Ryan A. Fontaine
Affiliation:
Department of Mechanical Science and Engineering, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA
Gregory S. Elliott
Affiliation:
Department of Aerospace Engineering, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA
Joanna M. Austin
Affiliation:
Department of Aerospace Engineering, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA
Jonathan B. Freund*
Affiliation:
Department of Mechanical Science and Engineering, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA Department of Aerospace Engineering, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

One of the principal challenges in the prediction and design of low-noise nozzles is accounting for the near-nozzle turbulent mixing layers at the high Reynolds numbers of engineering conditions. Even large-eddy simulation is a challenge because the locally largest scales are so small relative to the nozzle diameter. Model-scale experiments likewise typically have relatively thick near-nozzle shear layers, which potentially hampers their applicability to high-Reynolds-number design. 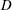To quantify the sensitivity of the far-field sound to nozzle turbulent-shear-layer conditions, a family of diameter $D$ nozzles is studied in which the exit turbulent boundary layer momentum thickness is varied from 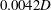$0.0042D$ up to 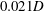$0.021D$ for otherwise identical flow conditions. Measurements include particle image velocimetry (PIV) to within 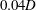$0.04D$ of the exit plane and far-field acoustic spectra. The influence of the initial turbulent-shear-layer thickness is pronounced, though it is less significant than the well-known sensitivity of the far-field sound to laminar versus turbulent shear-layer exit conditions. For thicker shear layers, the nominally missing region, where the corresponding thinner shear layer would develop, leads to the noise difference. The nozzle-exit momentum thickness successfully scales the high-frequency radiated sound for nozzles of different sizes and exhaust conditions. Yet, despite this success, the detailed turbulence statistics show distinct signatures of the different nozzle boundary layers from the different nozzles. Still, the different nozzle shear-layer thicknesses and shapes have a similar downstream development, which is consistent with a linear stability analysis of the measured velocity profiles.

JFM classification

Acoustics: Acoustics Boundary Layers: Boundary Layers Acoustics: Jet noise
Type
Papers
Information
Journal of Fluid Mechanics , Volume 770 , 10 May 2015 , pp. 27 - 51
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahuja, K. K.2003 Designing clean jet noise facilities and making accurate jet noise measurements. AIAA Paper 2003-706.Google Scholar
Ahuja, K. K. & Blakney, D. F. 1985 Tone excited jets, part IV: acoustic measurements. J. Sound Vib. 102 (1), 93–117.Google Scholar
Alkislar, M. B., Krothapalli, A. & Lourenco, L. M.2005 The effect of streamwise vorticity on the aeroacoustics of a Mach 0.9 axisymmetric jet. AIAA Paper 2005-3045.Google Scholar
ANSI 1995 Method for Calculation of the Absorption of Sound by the Atmosphere, ANSI s1.26-1995 edn American National Standards Institute.Google Scholar
ANSI 2004 Specification for Octave, Half-Octave, and Third Octave Band Filter Sets, ANSI s1.11-2004 edn American National Standards Institute.Google Scholar
Arakeri, V. H., Krothapalli, A., Siddavaram, V., Alkislar, M. B. & Lourenco, L. M. 2003 On the use of microjets to suppress turbulence in a Mach 0.9 axisymmetric jet. J. Fluid Mech. 490, 75–98.Google Scholar
ASME 1959 Fluid Meters, their Theory and Application, 5th edn. American Society of Mechanical Engineers.Google Scholar
Bodony, D. J. & Lele, S. K. 2005 On using large-eddy simulation for the prediction of noise from cold and heated turbulent jets. Phys. Fluids 17 (8), 085103.Google Scholar
Bogey, C. & Bailly, C. 2010 Influence of the nozzle-exit boundary-layer conditions on the flow and acoustic fields of initially laminar jets. J. Fluid Mech. 663, 507–538.Google Scholar
Bogey, C. & Marsden, O. 2013 Identification of the effects of the nozzle-exit boundary-layer thickness and its corresponding Reynolds number in initially highly disturbed subsonic jets. Phys. Fluids 25 (5), 055106.CrossRefGoogle Scholar
Bogey, C., Marsden, O. & Bailly, C. 2011 Large-eddy simulation of the flow and acoustic fields of a Reynolds number $10^{5}$ subsonic jet with tripped exit boundary layers. Phys. Fluids 23 (3), 035104.Google Scholar
Bogey, C., Marsden, O. & Bailly, C. 2012 Effects of moderate Reynolds numbers on subsonic round jets with highly disturbed nozzle-exit boundary layers. Phys. Fluids 24 (10), 105107.Google Scholar
Bradshaw, P. 1966 The effect of initial conditions on the development of a free shear layer. J. Fluid Mech. 26 (2), 225–236.Google Scholar
Bridges, J. & Brown, C. A.2004 Parametric testing of chevrons on single flow hot jets. NASA TM 2004-213107.Google Scholar
Bridges, J. E. & Hussain, A. K. M. F. 1987 Roles of initial condition and vortex pairing in jet noise. J. Sound Vib. 117 (2), 289–311.Google Scholar
Brown, C. & Bridges, J.2006 Small hot jet acoustic rig validation. NASA TM 2006-214234.Google Scholar
Brown, G. L. & Roshko, A. 1974 On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 64 (4), 775–816.Google Scholar
Cohen, J. & Wygnanski, I. 1987 The evolution of instabilities in the axisymmetric jet. Part 1. The linear growth of disturbances near the nozzle. J. Fluid Mech. 176, 191–219.Google Scholar
Concept Engineering Ltd 2011 Concept ViCount 180 Smoke System. Concept Engineering Ltd.Google Scholar
Crighton, D. G. & Huerre, P. 1990 Shear-layer pressure fluctuations and superdirective acoustic sources. J. Fluid Mech. 220, 355–368.Google Scholar
Ffowcs Williams, J. E. & Kempton, A. J. 1978 The noise from the large-scale structure of a jet. J. Fluid Mech. 84 (4), 673–694.Google Scholar
Fontaine, R. A.2014 Very near-nozzle shear-layer turbulence and jet noise. PhD thesis, University of Illinois at Urbana-Champaign.Google Scholar
Fontaine, R. A., Bobbitt, B., Austin, J. M., Elliott, G. S. & Freund, J. B.2012 Design and demonstration of a new small-scale jet noise experiment. AIAA Paper 2012-0682.Google Scholar
Freund, J. B. 2001 Noise sources in a low-Reynolds-number turbulent jet at Mach 0.9. J. Fluid Mech. 438, 277–305.Google Scholar
Freund, J. B., Lele, S. K. & Moin, P. 2000 Numerical simulation of a Mach 1.92 turbulent jet and its sound field. AIAA J. 38 (11), 2023–2031.Google Scholar
Freund, J. B. & Moin, P. 2000 Jet mixing enhancement by high-amplitude fluidic actuation. AIAA J. 38 (10), 1863–1870.Google Scholar
Freund, J. B., Moin, P. & Lele, S. K.1997 Compressibility effects in a turbulent annular mixing layer. Tech. Rep. TF-72. Stanford University, Mechanical Engineering, Flow Physics and Computation Division.Google Scholar
Gaster, M., Kit, E. & Wygnanski, I. 1985 Large-scale structures in a forced turbulent mixing layer. J. Fluid Mech. 150, 23–39.Google Scholar
Goldstein, M. E. & Leib, S. J. 2005 The role of instability waves in predicting jet noise. J. Fluid Mech. 525, 37–72.Google Scholar
Gropengeisser, H.1970 Study of the stability of boundary layers in compressible fluids. NASA Rep. TT-F-12.Google Scholar
Huerre, P. & Crighton, D. G.1983 Sound generation by instability waves in a low Mach number jet. AIAA Paper 1983-0661.Google Scholar
Humphreys, W. M. & Bartram, S. M. 2001 Measurement of separating flow structures using a multiple-camera DPIV system. In Instrumentation in Aerospace Simulation Facilities. 19th International Congress on ICIASF, pp. 82–93. IEEE.Google Scholar
Husain, Z. D. & Hussain, A. K. M. F. 1979 Axisymmetric mixing layer: influence of the initial and boundary conditions. AIAA J. 17 (1), 48–55.Google Scholar
Hussain, A. K. M. F. & Zaman, K. B. M. Q. 1985 An experimental study of organized motions in the turbulent plane mixing layer. J. Fluid Mech. 159, 85–104.Google Scholar
Hussain, A. K. M. F. & Zedan, M. F. 1978 Effects of the initial condition on the axisymmetric free shear layer: effects of the initial momentum thickness. Phys. Fluids 21 (7), 1100–1112.CrossRefGoogle Scholar
ISO 2003 Acoustics – Determination of Sound Power Levels of Noise Sources Using Sound Pressure – Precision Methods for Anechoic and Hemi-Anechoic Rooms, iso 3745 edn. International Organization for Standardization.Google Scholar
Janardan, B. A., Hoff, G. E., Barter, J. W., Martens, S., Gliebe, P. R., Mengle, V. & Dalton, W. N.2000 AST critical propulsion and noise reduction technologies for future commercial subsonic engines: separate-flow exhaust system noise reduction concept evaluation. NASA CR 2000-210039.Google Scholar
Jordan, P. & Colonius, T. 2013 Wave packets and turbulent jet noise. Annu. Rev. Fluid Mech. 45, 173–195.Google Scholar
Jubelin, B.1980 New experimental studies on jet noise amplification. AIAA Paper 1980-0961.CrossRefGoogle Scholar
Juvé, D., Sunyach, M. & Comte-Bellot, G. 1979 Filtered azimuthal correlations in the acoustic far field of a subsonic jet. AIAA J. 17 (1), 112–113.Google Scholar
Kerechanin, C. W. II 2000 The effects of nozzle trailing edge modifications on the acoustic far field of a Mach 2 rectangular jet. Master’s thesis, The Ohio State University, Columbus, OH.Google Scholar
Kim, J., Bodony, D. J. & Freund, J. B. 2014 Adjoint-based control of loud events in a turbulent jet. J. Fluid Mech. 741, 28–59.Google Scholar
Lazar, E., DeBlauw, B., Glumac, N., Dutton, C. & Elliott, G.2010 A practical approach to PIV uncertainty analysis. AIAA Paper 2010-4355.Google Scholar
Lilley, G. M. 1993 On the noise radiated from a turbulent high speed jet. In Computational Aeroacoustics (ed. Hardin, J. C. & Hussaini, M. Y.), pp. 85–115. Springer.Google Scholar
Lu, H. Y. 1983 Effect of excitation on coaxial jet noise. AIAA J. 21 (2), 214–220.Google Scholar
Maestrello, L. & McDaid, E. 1971 Acoustic characteristics of high-subsonic jets. AIAA J. 9 (6), 1058–1066.Google Scholar
Mankbadi, R. & Liu, J. T. C. 1984 Sound generated aerodynamically revisited: large-scale structures in a turbulent jet as a source of sound. Phil. Trans. R. Soc. Lond. A 311 (1516), 183–217.Google Scholar
Merkine, L. & Liu, J. T. C. 1975 On the development of noise producing large-scale wavelike eddies in a plane turbulent jet. J. Fluid Mech. 70 (2), 353–368.CrossRefGoogle Scholar
Michalke, A. & Fuchs, H. V. 1975 On turbulence and noise of an axisymmetric shear flow. J. Fluid Mech. 70 (1), 179–205.Google Scholar
Morris, S. C. & Foss, J. F. 2003 Turbulent boundary layer to single-stream shear layer: the transition region. J. Fluid Mech. 494, 187–221.Google Scholar
Narayanan, S., Barber, T. J. & Polak, D. R. 2002 High subsonic jet experiments: turbulence and noise generation studies. AIAA J. 40 (3), 430–437.Google Scholar
Nichols, J. W., Lele, S. K., Moin, P., Ham, F. E. & Bridges, J. E.2012 Large-eddy simulation for supersonic rectangular jet noise prediction: effects of chevrons. AIAA Paper 2012-2212.Google Scholar
Parekh, D. E., Kibens, V., Glezer, A., Wiltse, J. M. & Smith, D. M.1996 Innovative jet flow control – mixing enhancement experiments. AIAA Paper 1996-0308.CrossRefGoogle Scholar
Pope, A. & Harper, J. J. 1966 Low-Speed Wind Tunnel Testing. Wiley.Google Scholar
Reshotko, E., Saric, W. S. & Nagib, H. M.1997 Flow quality issues for large wind tunnels. AIAA Paper 1997-0225.Google Scholar
Ribner, H. S. 1969 Quadrupole correlations governing the pattern of jet noise. J. Fluid Mech. 38 (1), 1–24.Google Scholar
Roshko, A. 1993 Instability and turbulence in shear flows. In Theoretical and Applied Mechanics 1992 (ed. Bodner, S. R., Singer, J., Golan, A. & Hashin, Z.), Elsevier.Google Scholar
Samimy, M., Kim, J. H., Kastner, J., Adamovich, I. & Utkin, Y. 2007 Active control of high-speed and high-Reynolds-number jets using plasma actuators. J. Fluid Mech. 578, 305–330.Google Scholar
Sandberg, R. D., Sandham, N. D. & Suponitsky, V. 2012 Dns of compressible pipe flow exiting into a coflow. Intl J. Heat Fluid Flow 35, 33–44.Google Scholar
Sandham, N. D. & Reynolds, W. C. 1990 Compressible mixing layer: linear theory and direct simulation. AIAA J. 28 (4), 618–624.Google Scholar
Tam, C. K. W. & Auriault, L. 1999 Jet mixing noise from fine-scale turbulence. AIAA J. 37 (2), 145–153.Google Scholar
Tam, C. K. W. & Burton, D. E. 1984 Sound generated by instability waves of supersonic flows. Part 2. Axisymmetric jets. J. Fluid Mech. 138, 273–295.Google Scholar
Tam, C. K. W., Golebiowski, M. & Seiner, J. M.1996 On the two components of turbulent mixing noise from supersonic jets. AIAA Paper 1996-1716.Google Scholar
Uzun, A., Bin, J. & Hussaini, M. Y. 2011 High-fidelity numerical simulation of a chevron nozzle jet flow. Intl J. Aeroacoust. 10 (5–6), 531–564.Google Scholar
Uzun, A. & Hussaini, M. Y. 2009 Simulation of noise generation in near-nozzle region of a chevron nozzle jet. AIAA J. 47 (8), 1793–1810.Google Scholar
Viswanathan, K. 2004 Aeroacoustics of hot jets. J. Fluid Mech. 516, 39–82.Google Scholar
Viswanathan, K. 2006 Instrument considerations for accurate jet noise measurements. AIAA J. 44 (6), 1137–1149.Google Scholar
Viswanathan, K. & Clark, L. T. 2004 Effect of nozzle internal contour on jet aeroacoustics. Intl J. Aeroacoust. 3 (2), 103–135.Google Scholar
Viswanathan, K. & Morris, P. J. 1992 Predictions of turbulent mixing in axisymmetric compressible shear layers. AIAA J. 30 (6), 1529–1536.Google Scholar
Wang, M., Freund, J. B. & Lele, S. K. 2006 Computational prediction of flow-generated sound. Annu. Rev. Fluid Mech. 38, 483–512.Google Scholar
Zaman, K. B. M. Q. 1985a Effect of initial condition on subsonic jet noise. AIAA J. 23 (9), 1370–1373.Google Scholar
Zaman, K. B. M. Q. 1985b Far-field noise of a subsonic jet under controlled excitation. J. Fluid Mech. 152, 83–111.Google Scholar
Zaman, K. B. M. Q. 1986 Flow field and near and far sound field of a subsonic jet. J. Sound Vib. 106 (1), 1–16.Google Scholar
Zaman, K. B. M. Q. 2012 Effect of initial boundary-layer state on subsonic jet noise. AIAA J. 50 (8), 1784–1795.Google Scholar
Zaman, K. B. M. Q. & Hussain, A. K. M. F. 1980 Vortex pairing in a circular jet under controlled excitation. Part 1. General jet response. J. Fluid Mech. 101, 493–544.Google Scholar
Zaman, K. B. M. Q. & Hussain, A. K. M. F. 1981 Turbulence suppression in free shear flows by controlled excitation. J. Fluid Mech. 103, 133–159.Google Scholar