Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-17T11:25:29.320Z Has data issue: false hasContentIssue false
  • English
  • Français

Understanding discrete capillary-wave turbulence using a quasi-resonant kinetic equation

Published online by Cambridge University Press:  06 March 2017

Yulin Pan  and
Dick K. P. Yue Open the ORCID record for Dick K. P. Yue [Opens in a new window]
Yulin Pan
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Dick K. P. Yue*
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Experimental and numerical studies have shown that, with sufficient nonlinearity, the theoretical capillary-wave power-law spectrum derived from the kinetic equation (KE) of weak turbulence theory can be realized. This is despite the fact that the KE is derived assuming an infinite domain with continuous wavenumber, while experiments and numerical simulations are conducted in realistic finite domains with discrete wavenumbers for which the KE theoretically allows no energy transfer. To understand this, we first analyse results from direct simulations of the primitive Euler equations to elucidate the role of nonlinear resonance broadening (NRB) in discrete turbulence. We define a quantitative measure of the NRB, explaining its dependence on the nonlinearity level and its effect on the properties of the obtained stationary power-law spectra. This inspires us to develop a new quasi-resonant kinetic equation (QKE) for discrete turbulence, which incorporates the mechanism of NRB, governed by a single parameter $\unicode[STIX]{x1D705}$ expressing the ratio of NRB and wavenumber discreteness. At 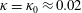$\unicode[STIX]{x1D705}=\unicode[STIX]{x1D705}_{0}\approx 0.02$, the QKE recovers simultaneously the spectral slope 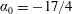$\unicode[STIX]{x1D6FC}_{0}=-17/4$ and the Kolmogorov constant 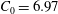$C_{0}=6.97$ (corrected from the original derivation) of the theoretical continuous spectrum, which physically represents the upper bound of energy cascade capacity for the discrete turbulence. For 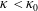$\unicode[STIX]{x1D705}<\unicode[STIX]{x1D705}_{0}$, the obtained spectra represent those corresponding to a finite domain with insufficient nonlinearity, resulting in a steeper spectral slope 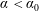$\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D6FC}_{0}$ and reduced capacity of energy cascade 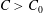$C>C_{0}$. The physical insights from the QKE are corroborated by direct simulation results of the Euler equations.

JFM classification

Waves/Free-surface Flows: Capillary waves Turbulent Flows: Turbulence theory Waves/Free-surface Flows: Waves/Free-surface Flows
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 816 , 10 April 2017 , R1
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Annenkov, S. Y. & Shrira, V. I. 2001 Numerical modelling of water-wave evolution based on the Zakharov equation. J. Fluid Mech. 449, 341–371.Google Scholar
Brazhnikov, M. Y., Kolmakov, G. V., Levchenko, A. A. & Mezhov-Deglin, L. P. 2002 Observation of capillary turbulence on the water surface in a wide range of frequencies. Europhys. Lett. 58 (4), 510.Google Scholar
Connaughton, C., Nazarenko, S. & Pushkarev, A. 2001 Discreteness and quasiresonances in weak turbulence of capillary waves. Phys. Rev. E 63 (4), 046306.Google Scholar
Deike, L., Bacri, J.-C. & Falcon, E. 2013 Nonlinear waves on the surface of a fluid covered by an elastic sheet. J. Fluid Mech. 733, 394–413.Google Scholar
Deike, L., Berhanu, M. & Falcon, E. 2014a Energy flux measurement from the dissipated energy in capillary wave turbulence. Phys. Rev. E 89 (6), 023003.Google Scholar
Deike, L., Daniel, F., Berhanu, M. & Falcon, E. 2014b Direct numerical simulations of capillary wave turbulence. Phys. Rev. Lett. 112 (1), 234501.Google Scholar
Denissenko, P., Lukaschuk, S. & Nazarenko, S. 2007 Gravity wave turbulence in a laboratory flume. Phys. Rev. Lett. 99 (1), 014501.Google Scholar
Dyachenko, S., Newell, A. C., Pushkarev, A. & Zakharov, V. E. 1992 Optical turbulence: weak turbulence, condensates and collapsing filaments in the nonlinear Schrödinger equation. Physica D 57 (1), 96–160.Google Scholar
Falcon, E., Laroche, C. & Fauve, S. 2007 Observation of gravity–capillary wave turbulence. Phys. Rev. Lett. 98 (9), 94503.Google Scholar
Galtier, S., Nazarenko, S. V., Newell, A. C. & Pouquet, A. 2002 Anisotropic turbulence of shear-Alfvén waves. Astrophys. J. Lett. 564 (1), L49.Google Scholar
Kartashova, E. A. 1990 Partitioning of ensembles of weakly interacting dispersing waves in resonators into disjoint classes. Physica D 46 (1), 43–56.Google Scholar
Lighthill, M. J. 1958 An Introduction to Fourier Analysis and Generalised Functions. Cambridge University Press.Google Scholar
Lvov, V. S. & Nazarenko, S. 2010 Discrete and mesoscopic regimes of finite-size wave turbulence. Phys. Rev. E 82 (5), 056322.Google Scholar
Lvov, Y. V., Polzin, K. L. & Tabak, E. G. 2004 Energy spectra of the ocean’s internal wave field: theory and observations. Phys. Rev. Lett. 92 (12), 128501.Google Scholar
Nazarenko, S. 2006 Sandpile behaviour in discrete water-wave turbulence. J. Stat. Mech. 2006 (02), L02002.Google Scholar
Nazarenko, S. 2011 Wave Turbulence, vol. 825. Springer Science and Business Media.Google Scholar
Newell, A. C. & Rumpf, B. 2011 Wave turbulence. Annu. Rev. Fluid Mech. 43, 59–78.Google Scholar
Pan, Y.2016 Understanding of weak turbulence of capillary waves. PhD thesis, Massachusetts Institute of Technology.Google Scholar
Pan, Y. & Yue, D. K. P. 2014 Direct numerical investigation of turbulence of capillary waves. Phys. Rev. Lett. 113 (9), 094501.Google Scholar
Pan, Y. & Yue, D. K. P. 2015 Decaying capillary wave turbulence under broad-scale dissipation. J. Fluid Mech. 780, R1.Google Scholar
Piscopia, R., Polnikov, V., DeGirolamo, P. & Magnaldi, S. 2003 Validation of the three-wave quasi-kinetic approximation for the spectral evolution in shallow water. Ocean Engng 30 (5), 579–599.Google Scholar
Polnikov, V. G. & Manenti, S. 2009 Study of relative roles of nonlinearity and depth refraction in wave spectrum evolution in shallow water. Engng Appl. Comput. Fluid Mech. 3 (1), 42–55.Google Scholar
Pushkarev, A., Resio, D. & Zakharov, V. 2003 Weak turbulent approach to the wind-generated gravity sea waves. Physica D 184 (1), 29–63.Google Scholar
Pushkarev, A. N. & Zakharov, V. E. 1996 Turbulence of capillary waves – theory and numerical simulation. Phys. Rev. Lett. 76 (18), 3320–3323.Google Scholar
Pushkarev, A. N & Zakharov, V. E. 2000 Physica D 135 (1), 98–116.Google Scholar
Wright, W. B., Budakian, R. & Putterman, S. J. 1996 Diffusing light photography of fully developed isotropic ripple turbulence. Phys. Rev. Lett. 76 (24), 4528–4531.Google Scholar
Xia, H., Shats, M. & Punzmann, H. 2010 Modulation instability and capillary wave turbulence. Europhys. Lett. 91 (1), 14002.Google Scholar
Zakharov, V. E. 2010 Energy balance in a wind-driven sea. Phys. Scr. 2010 (T142), 014052.Google Scholar
Zakharov, V. E. & Filonenko, N. N. 1966 The energy spectrum for stochastic oscillations of a fluid surface. Dokl. Akad. Nauk SSSR 170, 1292–1295.Google Scholar
Zakharov, V. E. & Filonenko, N. N. 1967 Weak turbulence of capillary waves. J. Appl. Mech. Tech. Phys. 8, 37–40.Google Scholar
Zakharov, V. E., L’vov, V. S. & Falkovich, G. 1992 Kolmogorov Spectra of Turbulence 1. Wave Turbulence, vol. 1, p. 275. Springer, ISBN: 3-540-54533-6.Google Scholar
Zaslavskii, M. M. & Polnikov, V. G 1998 Three-wave quasi-kinetic approximation in the problem of the evolution of a spectrum of nonlinear gravity waves at small depths. Izv. Atmos. Ocean. Phys. 34, 609–616.Google Scholar