Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-26T10:29:02.907Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent pair dispersion as a ballistic cascade phenomenology

Published online by Cambridge University Press:  08 May 2015

Mickaël Bourgoin
Mickaël Bourgoin*
Affiliation:
Laboratoire des Écoulements Géophysiques et Industriels, CNRS/UJF/G-INP, UMR 5519, Université de Grenoble, BP53, 38041, Grenoble, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Since the pioneering work of Richardson in 1926, later refined by Batchelor and Obukhov in 1950, it is predicted that the rate of separation of pairs of fluid elements in turbulent flows with initial separation at inertial scales, grows ballistically first (Batchelor regime), before undergoing a transition towards a super-diffusive regime where the mean-square separation grows as 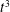$t^{3}$ (Richardson regime). Richardson empirically interpreted this super-diffusive regime in terms of a non-Fickian process with a scale-dependent diffusion coefficient (the celebrated Richardson’s ‘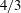$4/3$rd’ law). However, the actual physical mechanism at the origin of such a scale dependent diffusion coefficient remains unclear. The present article proposes a simple physical phenomenology for the time evolution of the mean-square relative separation in turbulent flows, based on a scale-dependent ballistic scenario rather than a scale-dependent diffusive. It is shown that this phenomenology accurately retrieves most of the known features of relative dispersion for particles mean-square separation, among others: (i) it is quantitatively consistent with most recent numerical simulations and experiments for mean-square separation between particles (both for the short-term Batchelor regime and the long-term Richardson regime, and for all initial separations at inertial scales); (ii) it gives a simple physical explanation of the origin of the super-diffusive 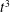$t^{3}$ Richardson regime which naturally builds itself as an iterative process of elementary short-term scale-dependent ballistic steps; (iii) it shows that the Richardson constant is directly related to the Kolmogorov constant (and eventually to a ballistic persistence parameter); and (iv) in a further extension of the phenomenology, taking into account third-order corrections, it robustly describes the temporal asymmetry between forward and backward dispersion, with an explicit connection to the cascade of energy flux across scales. An important aspect of this phenomenology is that it simply and robustly connects long-term super-diffusive features to elementary short-term mechanisms, and at the same time it connects basic Lagrangian features of turbulent relative dispersion (both at short and long times) to basic Eulerian features of the turbulent field: second-order Eulerian statistics control the growth of separation (both at short and long times) while third-order Eulerian statistics control the temporal asymmetry of the dispersion process, which can then be directly identified as the signature of the energy cascade and associated to well-known exact results as the Karman–Howarth–Monin relation.

JFM classification

Mixing: Mixing Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 772 , 10 June 2015 , pp. 678 - 704
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abecassis, B., Cottin-Bizonne, C., Ybert, C., Ajdari, A. & Bocquet, L. 2008 Boosting migration of large particles by solute contrasts. Nat. Mater. 7 (10), 785–789.Google Scholar
Batchelor, G. K. 1950 The application of the similarity theory of turbulence to atmospheric diffusion. Q. J. R. Meteorol. Soc. 76 (328), 133–146.Google Scholar
Berg, J., Lüthi, B., Mann, J. & Ott, S. 2006 Backwards and forwards relative dispersion in turbulent flow: an experimental investigation. Phys. Rev. E 74 (1), 016304.CrossRefGoogle ScholarPubMed
Biferale, L., Boffetta, G., Celani, A., Devenish, B. J., Lanotte, A. & Toschi, F. 2005 Lagrangian statistics of particles pairs in homogeneous isotropic turbulence. Phys. Fluids 17, 115101.Google Scholar
Bitane, R., Homann, H. & Bec, J. 2012 Time scales of turbulent relative dispersion. Phys. Rev. E 86 (4), 045302.Google Scholar
Boffetta, G. & Ecke, R. E. 2012 Two-dimensional turbulence. Annu. Rev. Fluid Mech. 44 (1), 427–451.CrossRefGoogle Scholar
Boffetta, G. & Sokolov, I. 2002a Relative dispersion in fully developed turbulence: the Richardsons law and intermittency corrections. Phys. Rev. Lett. 88 (9), 094501.Google Scholar
Boffetta, G. & Sokolov, I. M. 2002b Statistics of two-particle dispersion in two-dimensional turbulence. Phys. Fluids 14 (9), 3224–3232.CrossRefGoogle Scholar
Bourgoin, M., Ouellette, N. T., Xu, H., Berg, J. & Bodenschatz, E. 2006 The role of pair dispersion in turbulent flow. Science 311 (5762), 835–838.Google Scholar
Bragg, A. D., Ireland, P. J. & Collins, L. R.2014 Forward and backward in time dispersion of fluid and inertial particles in isotropic turbulence. Preprint arXiv:1403.5502 [physics.flu-dyn], p. 30.Google Scholar
Faber, T. & Vassilicos, J. C. 2009 Turbulent pair separation due to multiscale stagnation point structure and its time asymmetry in two-dimensional turbulence. Phys. Fluids 21 (1), 015106.Google Scholar
Frisch, U. 1995 Turbulence: The Legacy of A. N. Kolmogorov. Cambridge University Press.Google Scholar
Goto, S. & Vassilicos, J. C. 2004 Particle pair diffusion and persistent streamline topology in two-dimensional turbulence. New J. Phys. 6, 65, 1–35.CrossRefGoogle Scholar
Grossmann, S. 1990 Diffusion by turbulence. Ann. Phys. 47, 577–582.Google Scholar
Grossmann, S. & Procaccia, I. 1984 Unified theory of relative turbulent diffusion. Phys. Rev. A 29, 1358–1365.Google Scholar
Hill, R. J. 2006 Opportunities for use of exact statistical equations. J. Turbul. 7, 43, 1–13.Google Scholar
Jucha, J., Xu, H., Pumir, A. & Bodenschatz, E. 2014 Time-reversal-symmetry breaking in turbulence. Phys. Rev. Lett. 113 (5), 054501.Google Scholar
Jullien, M.-C., Paret, J. & Tabeling, P. 1999 Richardson pair dispersion in two-dimensional turbulence. Phys. Rev. Lett. 82 (14), 2872–2875.Google Scholar
Klafter, J., Blumen, A. & Shlesinger, M. F. 1987 Stochastic pathway to anomalous diffusion. Phys. Rev. E 35, 3081–3085.Google Scholar
Kolmogorov, A. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 301–305.Google Scholar
Lindborg, E. 1999 Can the atmospheric kinetic energy spectrum be explained by two-dimensional turbulence? J. Fluid Mech. 388, 259–288.Google Scholar
Mann, J., Ott, S. & Andersen, J. S.1999 Experimental study of relative, turbulent diffusion. Tech. Rep. Riso-R-1036 (EN). Risoe National Laboratory, Roskilde, Denmark.Google Scholar
Ott, S. & Mann, J. 2000 An experimental investigation of the relative diffusion of particle pairs in three-dimensional turbulent flow. J. Fluid Mech. 422, 207–223.Google Scholar
Ouellette, N. T., Xu, H., Bourgoin, M. & Bodenschatz, E. 2006 An experimental study of turbulent relative dispersion models. New J. Phys. 8 (6), 109, 1–23.Google Scholar
Rast, M. & Pinton, J.-F. 2009 Point-vortex model for Lagrangian intermittency in turbulence. Phys. Rev. E 79 (4), 046314.Google Scholar
Rast, M. P. & Pinton, J.-F. 2011 Pair dispersion in turbulence: the subdominant role of scaling. Phys. Rev. Lett. 107 (21), 214501.Google Scholar
Richardson, L. F. 1926 Atmospheric diffusion shown on a distance-neighbour graph. Proc. R. Soc. Lond. A 110 (756), 709–737.Google Scholar
Salazar, J. P. L. C. & Collins, L. R. 2009 Two-particle dispersion in isotropic turbulent flows. Annu. Rev. Fluid Mech. 41, 405–432.Google Scholar
Sawford, B. 2001 Turbulent relative dispersion. Annu. Rev. Fluid Mech. 33, 289–317.Google Scholar
Sawford, B. L., Yeung, P. K. & Borgas, M. S. 2005 Comparison of backwards and forwards relative dispersion in turbulence. Phys. Fluids 17 (9), 095109.Google Scholar
Sokolov, I. M. 1999 Two-particle dispersion by correlated random velocity fields. Phys. Rev. E 60 (5), 5528–5532.Google Scholar
Sokolov, I. M., Klafter, J. & Blumen, A. 2000 Ballistic versus diffusive pair dispersion in the Richardson regime. Phys. Rev. E 61 (3), 2717–2722.CrossRefGoogle Scholar
Sreenivasan, K. R. 1995 On the universality. Phys. Fluids 7 (3), 2778–2784.Google Scholar
Thalabard, S., Krstulovic, G. & Bec, J. 2014 Turbulent pair dispersion as a continuous-time random walk. J. Fluid Mech. 755, R4.CrossRefGoogle Scholar