Article contents
Tunable diffusion in wave-driven two-dimensional turbulence
Published online by Cambridge University Press: 27 February 2019
Abstract
We report an abrupt change in the diffusive transport of inertial objects in wave-driven turbulence as a function of the object size. In these non-equilibrium two-dimensional flows, the turbulent diffusion coefficient 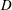 $D$ of finite-size objects undergoes a sharp change for values of the object size
$D$ of finite-size objects undergoes a sharp change for values of the object size 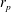 $r_{p}$ close to the flow forcing scale
$r_{p}$ close to the flow forcing scale 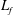 $L_{f}$. For objects larger than the forcing scale (
$L_{f}$. For objects larger than the forcing scale (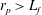 $r_{p}>L_{f}$), the diffusion coefficient is proportional to the flow energy
$r_{p}>L_{f}$), the diffusion coefficient is proportional to the flow energy 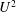 $U^{2}$ and inversely proportional to the size
$U^{2}$ and inversely proportional to the size 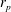 $r_{p}$. This behaviour,
$r_{p}$. This behaviour, 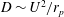 $D\sim U^{2}/r_{p}$ , observed in a chaotic macroscopic system is reminiscent of a fluctuation–dissipation relation. In contrast, the diffusion coefficient of smaller objects (
$D\sim U^{2}/r_{p}$ , observed in a chaotic macroscopic system is reminiscent of a fluctuation–dissipation relation. In contrast, the diffusion coefficient of smaller objects (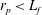 $r_{p}<L_{f}$) follows
$r_{p}<L_{f}$) follows 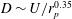 $D\sim U/r_{p}^{0.35}$. This result does not allow simple analogies to be drawn but instead it reflects strong coupling of the small objects with the fabric and memory of the out-of-equilibrium flow. In these turbulent flows, the flow structure is dominated by transient but long-living bundles of fluid particle trajectories executing random walk. The characteristic widths of the bundles are close to
$D\sim U/r_{p}^{0.35}$. This result does not allow simple analogies to be drawn but instead it reflects strong coupling of the small objects with the fabric and memory of the out-of-equilibrium flow. In these turbulent flows, the flow structure is dominated by transient but long-living bundles of fluid particle trajectories executing random walk. The characteristic widths of the bundles are close to 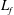 $L_{f}$. We propose a simple phenomenology in which large objects interact with many bundles. This interaction with many degrees of freedom is the source of the fluctuation–dissipation-like relation. In contrast, smaller objects are advected within coherent bundles, resulting in diffusion properties closely related to those of fluid tracers.
$L_{f}$. We propose a simple phenomenology in which large objects interact with many bundles. This interaction with many degrees of freedom is the source of the fluctuation–dissipation-like relation. In contrast, smaller objects are advected within coherent bundles, resulting in diffusion properties closely related to those of fluid tracers.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 13
- Cited by


