Article contents
Transient flows and migration in granular suspensions: key role of Reynolds-like dilatancy
Published online by Cambridge University Press: 23 September 2022
Abstract
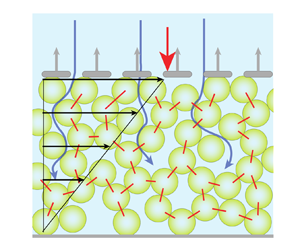
We investigate the transient dynamics of a sheared suspension of neutrally buoyant particles in pressure-imposed rheology configuration, subject to a sudden change in shear rate or external pressure. Discrete element method simulations show that, depending on the flow parameters (particle and system size, initial volume fraction), the early stress response of the suspension may differ strongly from the prediction of the suspension balance model based on the steady-state rheology. We show that a two-phase model incorporating the Reynolds-like dilatancy law of Pailha & Pouliquen (J. Fluid Mech., vol. 633, 2009, pp. 115–135), which prescribes the dilation rate of the suspension over a strain scale  $\gamma _0$, captures quantitatively the suspension dilation/compaction over the whole range of parameters investigated. Together with the Darcy flow induced by the pore pressure gradient during dilation or compaction, this Reynolds-like dilatancy implies that the early stress response of the suspension is non-local, with a non-local length scale
$\gamma _0$, captures quantitatively the suspension dilation/compaction over the whole range of parameters investigated. Together with the Darcy flow induced by the pore pressure gradient during dilation or compaction, this Reynolds-like dilatancy implies that the early stress response of the suspension is non-local, with a non-local length scale  $\ell$ that scales with the particle size and diverges algebraically at jamming. In regions affected by
$\ell$ that scales with the particle size and diverges algebraically at jamming. In regions affected by  $\ell$, the stress level is fixed, not by the steady-state rheology, but by the Darcy fluid pressure gradient resulting from the dilation/compaction rate. Our results extend the validity of the Reynolds-like dilatancy flow rule, initially proposed for jammed suspensions, to flowing suspension below the critical volume fraction at which the suspension jams, thereby providing a unified framework to describe dilation and shear-induced migration. They pave the way for understanding more complex unsteady flows of dense suspensions, such as impacts, transient avalanches or the impulsive response of shear-thickening suspensions.
$\ell$, the stress level is fixed, not by the steady-state rheology, but by the Darcy fluid pressure gradient resulting from the dilation/compaction rate. Our results extend the validity of the Reynolds-like dilatancy flow rule, initially proposed for jammed suspensions, to flowing suspension below the critical volume fraction at which the suspension jams, thereby providing a unified framework to describe dilation and shear-induced migration. They pave the way for understanding more complex unsteady flows of dense suspensions, such as impacts, transient avalanches or the impulsive response of shear-thickening suspensions.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
REFERENCES
- 6
- Cited by



