Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-06T00:23:15.190Z Has data issue: false hasContentIssue false
  • English
  • Français

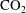$\text{CO}_{2}$ dissolution in a background hydrological flow

Published online by Cambridge University Press:  26 January 2016

H. Juliette T. Unwin ,
Garth N. Wells  and
Andrew W. Woods
H. Juliette T. Unwin
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
Garth N. Wells
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
Andrew W. Woods*
Affiliation:
BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

During 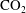$\text{CO}_{2}$ sequestration into a deep saline aquifer of finite vertical extent, 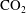$\text{CO}_{2}$ will tend to accumulate in structural highs such as offered by an anticline. Over times of tens to thousands of years, some of the 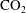$\text{CO}_{2}$ will dissolve into the underlying groundwater to produce a region of relatively dense, saturated water directly below the plume of 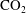$\text{CO}_{2}$. Continued dissolution then requires the supply of unsaturated aquifer water. In an aquifer of finite vertical extent, this may be provided by a background hydrological flow, or a laterally-spreading buoyancy-driven flow caused by the greater density of the 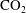$\text{CO}_{2}$ saturated water relative to the original aquifer water.

We investigate long time steady-state dissolution in the presence of a background hydrological flow. In steady state, the distribution of 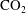$\text{CO}_{2}$ in the groundwater upstream of the aquifer involves a balance between three competing effects: (i) the buoyancy-driven flow of 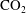$\text{CO}_{2}$ saturated water; (ii) the diffusion of 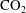$\text{CO}_{2}$ from saturated to under-saturated water; and (iii) the advection associated with the oncoming background flow. This leads to three limiting regimes. In the limit of very slow diffusion, a nearly static intrusion of dense fluid may extend a finite distance upstream, balanced by the pressure gradient associated with the oncoming background flow. In the limit of fast diffusion relative to the flow, a gradient zone may become established in which the along-aquifer diffusive flux balances the advection associated with the background flow. However, if the buoyancy-driven flow speed exceeds the background hydrological flow speed, then a third, intermediate regime may become established. In this regime, a convective recirculation develops upstream of the anticline involving the vertical diffusion of 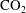$\text{CO}_{2}$ from an upstream propagating flow of dense 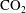$\text{CO}_{2}$ saturated water into the downstream propagating flow of 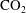$\text{CO}_{2}$ unsaturated water. For each limiting case, we find analytical solutions for the distribution of 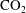$\text{CO}_{2}$ upstream of the anticline, and test our analysis with full numerical simulations. A key result is that, although there may be very different controls on the distribution and extent of 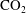$\text{CO}_{2}$ bearing water upstream of the anticline, in each case the dissolution rate is given by the product of the background volume flux and the difference in concentration between the 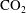$\text{CO}_{2}$ saturated water and the original aquifer water upstream.

JFM classification

Geophysical and Geological Flows: Gravity currents Low-Reynolds-number flows: Porous media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 789 , 25 February 2016 , pp. 768 - 784
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bear, J. 1972 Dynamics of Fluids in Porous Media. Courier Corporation.Google Scholar
Boait, F. C., White, N. J., Bickle, M. J., Chadwick, R. A., Neufeld, J. A. & Huppert, H. E. 2012 Spatial and temporal evolution of injected $\text{CO}_{2}$ at the Sleipner Field, North Sea. J. Geophys. Res. 117 (B3), B03309.Google Scholar
Hesse, M. A., Tchelepi, H. A., Cantwel, B. J. & Orr, F. M. 2007 Gravity currents in horizontal porous layers: transition from early to late self-similarity. J. Fluid Mech. 577, 363–383.CrossRefGoogle Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2014 High rayleigh number convection in a three-dimensional porous medium. J. Fluid Mech. 748, 879–895.CrossRefGoogle Scholar
Huppert, H. E. & Woods, A. W. 1995 Gravity-driven flows in porous layers. J. Fluid Mech. 292, 55–69.CrossRefGoogle Scholar
IPCC2005 Carbon dioxide capture and storage. IPCC Geneva, Switzerland, https://www.ipcc.ch/publications_and_data/_reports_carbon_dioxide.htm.Google Scholar
Lindeberg, E. & Wessel-Berg, D. 1997 Vertical convection in an aquifer column under a gas cap of $\text{CO}_{2}$ . Energy Convers. Manage. 38, S229–S234; Proc. 3rd Int. Conf. on Carbon Dioxide Removal.CrossRefGoogle Scholar
Logg, A., Mardal, K.-A. & Wells, G. N.(Eds) 2012 Automated Solution of Differential Equations by the Finite Element Method, Lecture Notes in Computational Science and Engineering, vol. 84. Springer.CrossRefGoogle Scholar
Pau, G. S. H., Bell, J. B., Pruess, K. S., Almgren, A. J., Lijewsji, M. & Zhang, K. 2009 Numerical studies of density-driven flow in $\text{CO}_{2}$ storage in saline aquifers. In TOUGH Symposium 2009.Google Scholar
Pruess, K., Xu, T., Apps, J. & Garcia, J. 2003 Numerical modeling of aquifer disposal of $\text{CO}_{2}$ . Soc. Petrol. Engng J. 8, 49–60.Google Scholar
Riaz, A., Hesse, M., Tchelepi, H. A. & Orr, F. M. 2006 Onset of convection in a gravitationally unstable diffusive boundary layer in porous media. J. Fluid Mech. 548, 87–111.CrossRefGoogle Scholar
Szulczewski, M. L., Hesse, M. A. & Juanes, R. 2013 Carbon dioxide dissolution in structural and stratigraphic traps. J. Fluid Mech. 736, 287–315.CrossRefGoogle Scholar
Taylor, G. 1953 Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond. A 219 (1137), 186–203.Google Scholar
Unwin, H. J. T. & Wells, G. N.2015 Supporting material. https://www.repository.cam.ac.uk/handle/1810/252804.Google Scholar
Verdon, J. P., Kendall, J.-M., Stork, A. L., Chadwick, R. A., White, D. J. & Bissell, R. C. 2013 Comparison of geomechanical deformation induced by megatonne-scale $\text{CO}_{2}$ storage at Sleipner, Weyburn, and In Salah. Proc. Natl Acad. Sci. USA 110 (30), E2762–E2771.CrossRefGoogle Scholar
Woods, A. W. 2015 Flow in Porous Rock. Cambridge University Press.Google Scholar
Woods, A. W. & Espie, T. 2012 Controls on the dissolution of $\text{CO}_{2}$ plumes in structural traps in deep saline aquifers. Geophys. Res. Lett. 39 (8), L08401.CrossRefGoogle Scholar