Published online by Cambridge University Press: 06 June 2016
The internal waves (IWs) radiated by the turbulent wake of a sphere of diameter 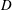 $D$ towed at speed
$D$ towed at speed 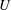 $U$ are investigated using three-dimensional fully nonlinear simulations performed in a linearly stratified Boussinesq fluid with buoyancy frequency
$U$ are investigated using three-dimensional fully nonlinear simulations performed in a linearly stratified Boussinesq fluid with buoyancy frequency 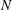 $N$. The study focuses on a broad range of wave characteristics in the far field of the turbulent wave source, specifically at the sea surface (as modelled by a free-slip rigid lid) where the IWs reflect. Six simulations are performed at Reynolds number
$N$. The study focuses on a broad range of wave characteristics in the far field of the turbulent wave source, specifically at the sea surface (as modelled by a free-slip rigid lid) where the IWs reflect. Six simulations are performed at Reynolds number 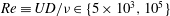 $Re\equiv UD/{\it\nu}\in \{5\times 10^{3},10^{5}\}$ and Froude number
$Re\equiv UD/{\it\nu}\in \{5\times 10^{3},10^{5}\}$ and Froude number 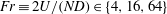 $Fr\equiv 2U/(ND)\in \{4,16,64\}$, where
$Fr\equiv 2U/(ND)\in \{4,16,64\}$, where  ${\it\nu}$ is viscosity. The wave-emitting wake is located at a fixed distance of
${\it\nu}$ is viscosity. The wave-emitting wake is located at a fixed distance of 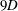 $9D$ below the surface. As the wake evolves for up to
$9D$ below the surface. As the wake evolves for up to 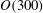 $O(300)$ units of buoyancy time scale
$O(300)$ units of buoyancy time scale 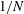 $1/N$, IW characteristics, such as horizontal wavelength
$1/N$, IW characteristics, such as horizontal wavelength 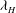 ${\it\lambda}_{H}$ and wave period
${\it\lambda}_{H}$ and wave period 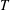 $T$, are sampled at the sea surface via wavelet transforms of horizontal divergence signals. The statistics of amplitudes and orientations of IW-induced surface strains are also reported. The mean dimensionless observable wavelength
$T$, are sampled at the sea surface via wavelet transforms of horizontal divergence signals. The statistics of amplitudes and orientations of IW-induced surface strains are also reported. The mean dimensionless observable wavelength 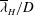 $\overline{{\it\lambda}}_{H}/D$ at the sea surface decays in time as
$\overline{{\it\lambda}}_{H}/D$ at the sea surface decays in time as 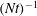 $(Nt)^{-1}$, which is due to the waves’ dispersion. This observation is in agreement with a linear propagation model that is independent of the wake
$(Nt)^{-1}$, which is due to the waves’ dispersion. This observation is in agreement with a linear propagation model that is independent of the wake 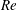 $Re$ and
$Re$ and 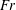 $Fr$. This agreement further suggests that the most energetic waves impacting the surface originate from the early-time wake that is adjusting to buoyancy. The most energetic dimensionless wavelength
$Fr$. This agreement further suggests that the most energetic waves impacting the surface originate from the early-time wake that is adjusting to buoyancy. The most energetic dimensionless wavelength 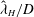 $\hat{{\it\lambda}}_{H}/D$ is found to scale as
$\hat{{\it\lambda}}_{H}/D$ is found to scale as 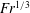 $Fr^{1/3}$ and decrease with
$Fr^{1/3}$ and decrease with 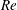 $Re$, which causes the arrival time (in
$Re$, which causes the arrival time (in 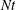 $Nt$ units) of the strongest waves at the surface to scale as
$Nt$ units) of the strongest waves at the surface to scale as 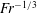 $Fr^{-1/3}$ and increase with
$Fr^{-1/3}$ and increase with 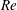 $Re$. This wavelength
$Re$. This wavelength 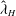 $\hat{{\it\lambda}}_{H}$ is also found to correlate with the vertical Taylor scale of the wake turbulence. IW-driven phenomena at the surface that are of interest to an observer, such as the local enrichment of surfactant and the transport of ocean surface tracers, are also examined. The local enrichment ratio of surface scalar scales linearly with the steepness of IWs that reach the surface, and the ratio often exceeds a possible visibility threshold. The Lagrangian drifts of ocean tracers, which are linked to the nonlinear interaction between incident and reflecting IW packets, create a local divergence in lateral mass transport right above the wake centreline, an effect that intensifies strongly with increasing
$\hat{{\it\lambda}}_{H}$ is also found to correlate with the vertical Taylor scale of the wake turbulence. IW-driven phenomena at the surface that are of interest to an observer, such as the local enrichment of surfactant and the transport of ocean surface tracers, are also examined. The local enrichment ratio of surface scalar scales linearly with the steepness of IWs that reach the surface, and the ratio often exceeds a possible visibility threshold. The Lagrangian drifts of ocean tracers, which are linked to the nonlinear interaction between incident and reflecting IW packets, create a local divergence in lateral mass transport right above the wake centreline, an effect that intensifies strongly with increasing 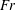 $Fr$. The findings of this study may serve as a platform to investigate the generation and surface manifestation of IWs radiated by other canonical submerged stratified turbulent flows.
$Fr$. The findings of this study may serve as a platform to investigate the generation and surface manifestation of IWs radiated by other canonical submerged stratified turbulent flows.