Article contents
Superfast amplification and superfast nonlinear saturation of perturbations as a mechanism of turbulence
Published online by Cambridge University Press: 15 October 2020
Abstract
Ruelle predicted that the maximal amplification of perturbations in homogeneous isotropic turbulence is exponential  $\exp ({\sigma \sqrt {Re} \,t})$ (where
$\exp ({\sigma \sqrt {Re} \,t})$ (where  $\sigma \sqrt {Re}$ is the maximal Lyapunov exponent). In our earlier works, we predicted that the maximal amplification of perturbations in fully developed turbulence is faster than exponential and is given by
$\sigma \sqrt {Re}$ is the maximal Lyapunov exponent). In our earlier works, we predicted that the maximal amplification of perturbations in fully developed turbulence is faster than exponential and is given by  $\exp ({\sigma \sqrt {Re} \sqrt {t} +\sigma _1 t})$ where
$\exp ({\sigma \sqrt {Re} \sqrt {t} +\sigma _1 t})$ where  $\sigma \sqrt {Re} \sqrt {t}$ is much larger than
$\sigma \sqrt {Re} \sqrt {t}$ is much larger than  $\sigma \sqrt {Re} \, t$ for small
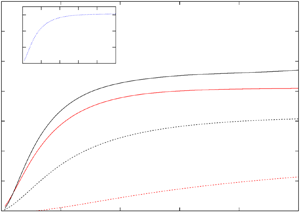
$\sigma \sqrt {Re} \, t$ for small  $t$. That is, we predicted superfast initial amplification of perturbations. Built upon our earlier numerical verification of our prediction, here, we conduct a large numerical verification with resolution up to
$t$. That is, we predicted superfast initial amplification of perturbations. Built upon our earlier numerical verification of our prediction, here, we conduct a large numerical verification with resolution up to  $2048^3$ and Reynolds number up to
$2048^3$ and Reynolds number up to  $6210$. Our direct numerical simulation here confirms our analytical prediction. Our numerical simulation also demonstrates that such superfast amplification of perturbations leads to superfast nonlinear saturation. We conclude that such superfast amplification and superfast nonlinear saturation of ever existing perturbations suggest a mechanism for the generation, development and persistence of fully developed turbulence.
$6210$. Our direct numerical simulation here confirms our analytical prediction. Our numerical simulation also demonstrates that such superfast amplification of perturbations leads to superfast nonlinear saturation. We conclude that such superfast amplification and superfast nonlinear saturation of ever existing perturbations suggest a mechanism for the generation, development and persistence of fully developed turbulence.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
Footnotes
Present address: Marian Smoluchowski Institute of Theoretical Physics, Jagiellonian University, Lojasiewicza 11, 30-348 Krakow, Poland.
References
REFERENCES
- 10
- Cited by



