Published online by Cambridge University Press: 15 May 2019
This paper follows a recent article of Nambiar et al. (J. Fluid Mech., vol. 812, 2017, pp. 41–64) on the linear rheological response of a dilute bacterial suspension (e.g. E. coli) to impulsive starting and stopping of simple shear flow. Here, we analyse the time dependent nonlinear rheology for a pair of linear flows – simple shear (a canonical weak flow) and uniaxial extension (a canonical strong flow), again in response to impulsive initiation and cessation. The rheology is governed by the bacterium orientation distribution which satisfies a kinetic equation that includes rotation by the imposed flow, and relaxation to isotropy via rotary diffusion and tumbling. The relevant dimensionless parameters are the Péclet number 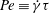 $Pe\equiv \dot{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D70F}$, which dictates the importance of flow-induced orientation anisotropy, and
$Pe\equiv \dot{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D70F}$, which dictates the importance of flow-induced orientation anisotropy, and 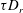 $\unicode[STIX]{x1D70F}D_{r}$, which quantifies the relative importance of the two intrinsic orientation decorrelation mechanisms (tumbling and rotary diffusion). Here,
$\unicode[STIX]{x1D70F}D_{r}$, which quantifies the relative importance of the two intrinsic orientation decorrelation mechanisms (tumbling and rotary diffusion). Here,  $\unicode[STIX]{x1D70F}$ is the mean run duration of a bacterium that exhibits a run-and-tumble dynamics,
$\unicode[STIX]{x1D70F}$ is the mean run duration of a bacterium that exhibits a run-and-tumble dynamics, 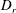 $D_{r}$ is the intrinsic rotary diffusivity of the bacterium and
$D_{r}$ is the intrinsic rotary diffusivity of the bacterium and 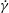 $\dot{\unicode[STIX]{x1D6FE}}$ is the characteristic magnitude of the imposed velocity gradient. The solution of the kinetic equation is obtained numerically using a spectral Galerkin method, that yields the rheological properties (the shear viscosity, the first and second normal stress differences for simple shear, and the extensional viscosity for uniaxial extension) over the entire range of
$\dot{\unicode[STIX]{x1D6FE}}$ is the characteristic magnitude of the imposed velocity gradient. The solution of the kinetic equation is obtained numerically using a spectral Galerkin method, that yields the rheological properties (the shear viscosity, the first and second normal stress differences for simple shear, and the extensional viscosity for uniaxial extension) over the entire range of 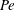 $Pe$. For simple shear, we find that the stress relaxation predicted by our analysis at small
$Pe$. For simple shear, we find that the stress relaxation predicted by our analysis at small 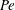 $Pe$ is in good agreement with the experimental observations of Lopez et al. (Phys. Rev. Lett., vol. 115, 2015, 028301). However, the analysis at large
$Pe$ is in good agreement with the experimental observations of Lopez et al. (Phys. Rev. Lett., vol. 115, 2015, 028301). However, the analysis at large 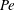 $Pe$ yields relaxations that are qualitatively different. Upon step initiation of shear, the rheological response in the experiments corresponds to a transition from a nearly isotropic suspension of active swimmers at small
$Pe$ yields relaxations that are qualitatively different. Upon step initiation of shear, the rheological response in the experiments corresponds to a transition from a nearly isotropic suspension of active swimmers at small 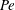 $Pe$, to an apparently (nearly) isotropic suspension of passive rods at large
$Pe$, to an apparently (nearly) isotropic suspension of passive rods at large 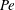 $Pe$. In contrast, the computations yield the expected transition to a nearly flow-aligned suspension of passive rigid rods at high
$Pe$. In contrast, the computations yield the expected transition to a nearly flow-aligned suspension of passive rigid rods at high 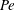 $Pe$. We probe this active–passive transition systematically, complementing the numerical solution with analytical solutions obtained from perturbation expansions about appropriate base states. Our study suggests courses for future experimental and analytical studies that will help understand relaxation phenomena in active suspensions.
$Pe$. We probe this active–passive transition systematically, complementing the numerical solution with analytical solutions obtained from perturbation expansions about appropriate base states. Our study suggests courses for future experimental and analytical studies that will help understand relaxation phenomena in active suspensions.