Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-19T05:55:21.665Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability analysis of experimental flow fields behind a porous cylinder for the investigation of the large-scale wake vortices

Published online by Cambridge University Press:  09 January 2013

Simone Camarri ,
Bengt E. G. Fallenius  and
Jens H. M. Fransson
Simone Camarri*
Affiliation:
Dipartimento di Ingegneria Aerospaziale, Università di Pisa, via G. Caruso N. 8, 56122 Pisa, Italy
Bengt E. G. Fallenius
Affiliation:
Linné Flow Centre, KTH Mechanics, SE-100 44 Stockholm, Sweden
Jens H. M. Fransson
Affiliation:
Linné Flow Centre, KTH Mechanics, SE-100 44 Stockholm, Sweden
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

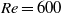When the linear stability analysis is applied to the time-averaged flow past a circular cylinder after the primary instability of the wake, a nearly marginally stable global mode is predicted with a frequency in time equal to that of the saturated vortex shedding. This behaviour has recently been shown to hold up to Reynolds number $\mathit{Re}= 600$ by direct numerical simulations. In the present work we verify that the global stability analysis provides reasonable estimation also when applied to experimental velocity fields measured in the wake past a porous circular cylinder at 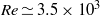$\mathit{Re}\simeq 3. 5\ensuremath{\times} 1{0}^{3} $. Different intensities of continuous suction and blowing through the entire surface of the cylinder are considered. The global direct and adjoint stability modes, derived from the experimental data, are used to sort the random instantaneous snapshots of the velocity field in phase. The proposed method is remarkable, sorting the snapshots in phase with respect to the vortex shedding, allowing phase-averaged velocity fields to be extracted from the experimental database. The phase-averaged flow fields are analysed in order to study the effect of the transpiration on the kinematical characteristics of the large-scale wake vortices.

JFM classification

Instability: Instability Vortex Flows: Vortex shedding Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 715 , 25 January 2013 , pp. 499 - 536
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barkley, D. 2006 Linear analysis of the cylinder wake mean flow. Europhys. Lett. 75 (5), 750–756.Google Scholar
Fallenius, B. E. G. 2011 Experimental design and vortex analyses in turbulent wake flows. PhD thesis, Royal Institute of Technology (KTH), Stockholm; TRITA-MEK Tech. Rep. 2011:12.Google Scholar
Fischer, P. F. & Kerkemeier, S. G. 2008 nek5000, web page. http://nek5000.mcs.anl.gov.Google Scholar
Fransson, J. H. M. & Alfredsson, P. H. 2003 On the disturbance growth in an asymptotic suction boundary layer. J. Fluid Mech. 482, 51–90.Google Scholar
Fransson, J., Konieczny, P. & Alfredsson, P. 2004 Flow around a porous cylinder subject to continuous suction or blowing. J. Fluids Struct. 19 (8), 1031–1048.Google Scholar
Giannetti, F., Camarri, S. & Luchini, P. 2010 Structural sensitivity of the secondary instability in the wake of a circular cylinder. J. Fluid Mech. 651, 319–337.CrossRefGoogle Scholar
Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.Google Scholar
Hernàndez, V., Romàn, J. E., Romero, E. & Vidal, A. T. V. 2009 SLEPc Users Manual, Scalable library for eigenvalue problem computations. Tech. Rep. Universidad Politecnica de Valencia.Google Scholar
Juniper, M. P., Tammisola, O. & Lundell, F. 2011 The local and global stability of confined planar wakes at intermediate Reynolds number. J. Fluid Mech. 686, 218–238.CrossRefGoogle Scholar
Leontini, J. S., Thompson, M. C. & Hourigan, K. 2010 A numerical study of global frequency selection in the time-mean wake of a circular cylinder. J. Fluid Mech. 645, 435–446.Google Scholar
Lindgren, B. 2002 Flow facility design and experimental studies of wall-bounded turbulent shear-flows. PhD thesis, Royal Institute of Technology (KTH), Stockholm; TRITA-MEK Tech. Rep. 2002:16.Google Scholar
Malkus, W. V. R. 1956 Outline of a theory of turbulent shear flow. J. Fluid Mech. 1, 521–539.CrossRefGoogle Scholar
Marquet, O., Sipp, D. & Jacquin, L. 2008 Sensitivity analysis and passive control of cylinder flows. J. Fluid Mech. 615, 221–252.Google Scholar
Mathelin, L., Bataille, F. & Lallemand, A. 2001 Near wake of a circular cylinder submitted to blowing – II. Impact on dynamics. Intl J. Heat Mass Transfer 44, 3709–3719.CrossRefGoogle Scholar
Meliga, P., Pujals, G. & Serre, E. 2012 Sensitivity of 2-D turbulent flow past a D-shaped cylinder using global stability. Phys. Fluids 24, 061701.Google Scholar
Noack, B. R., Afanasiev, K., Morzynski, M., Tadmor, G. & Thiele, F. 2003 A hierarchy of low-dimensional models for the transient and post-transient cylinder wake. J. Fluid Mech. 497, 335–363.CrossRefGoogle Scholar
Oberleithner, K., Sieber, M., Nayeri, C. N., Paschereit, C. O., Petz, C., Hege, H.-C., Noack, B. R. & Wygnanski, I. 2011 Three-dimensional coherent structures in a swirling jet undergoing vortex breakdown: stability analysis and empirical mode construction. J. Fluid Mech. 679, 383–414.Google Scholar
Pujals, G., Garcia-Villalba, M., Cossu, C. & Depardon, S. 2009 A note on optimal transient growth in turbulent channel flows. Phys. Fluids 21, 015109.CrossRefGoogle Scholar
Sipp, D. & Lebedev, A. 2007 Global stability of base and mean flows: a general approach and its applications to cylinder and open cavity flows. J. Fluid Mech. 593, 333–358.Google Scholar
Schmid, P. J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 2–28.Google Scholar
Schmid, P. J., Li, L., Juniper, M. P. & Prust, O. 2011 Applications of the dynamic mode decomposition. Theor. Comput. Fluid Dyn. 25, 249–259.Google Scholar
Wu, J.-Z., Xiong, A.-K. & Yang, Y.-T. 2005 Axial stretching and vortex definition. Phys. Fluids 17 (3), 038108.Google Scholar
Zdravkovich, M. M. 1997 Flow Around Circular Cylinders – Vol. 1: Fundamentals. Oxford Science Publications.Google Scholar