Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-16T18:00:57.722Z Has data issue: false hasContentIssue false
  • English
  • Français

A squirmer across Reynolds numbers

Published online by Cambridge University Press:  29 April 2016

Nicholas G. Chisholm ,
Dominique Legendre ,
Eric Lauga  and
Aditya S. Khair
Nicholas G. Chisholm
Affiliation:
Department of Chemical Engineering, Carnegie Mellon University, Pittsburgh, PA 15213, USA
Dominique Legendre
Affiliation:
IMFT (Institut de Mécanique des Fluides de Toulouse), Université de Toulouse, INPT-UPS, Allée Camille Soula, F-31400 Toulouse, France
Eric Lauga
Affiliation:
Department of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
Aditya S. Khair*
Affiliation:
Department of Chemical Engineering, Carnegie Mellon University, Pittsburgh, PA 15213, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

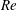The self-propulsion of a spherical squirmer – a model swimming organism that achieves locomotion via steady tangential movement of its surface – is quantified across the transition from viscously to inertially dominated flow. Specifically, the flow around a squirmer is computed for Reynolds numbers ($Re$) between 0.01 and 1000 by numerical solution of the Navier–Stokes equations. A squirmer with a fixed swimming stroke and fixed swimming direction is considered. We find that fluid inertia leads to profound differences in the locomotion of pusher (propelled from the rear) versus puller (propelled from the front) squirmers. Specifically, pushers have a swimming speed that increases monotonically with 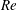$Re$, and efficient convection of vorticity past their surface leads to steady axisymmetric flow that remains stable up to at least 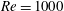$Re=1000$. In contrast, pullers have a swimming speed that is non-monotonic with 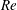$Re$. Moreover, they trap vorticity within their wake, which leads to flow instabilities that cause a decrease in the time-averaged swimming speed at large 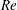$Re$. The power expenditure and swimming efficiency are also computed. We show that pushers are more efficient at large 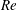$Re$, mainly because the flow around them can remain stable to much greater 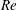$Re$ than is the case for pullers. Interestingly, if unstable axisymmetric flows at large 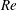$Re$ are considered, pullers are more efficient due to the development of a Hill’s vortex-like wake structure.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Biological Fluid Dynamics: Propulsion Biological Fluid Dynamics: Swimming/flying
Type
Papers
Information
Journal of Fluid Mechanics , Volume 796 , 10 June 2016 , pp. 233 - 256
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abraham, F. F. 1970 Functional dependence of drag coefficient of a sphere on Reynolds number. Phys. Fluids 13 (8), 2194–2195.Google Scholar
Afanasyev, Y. D. 2004 Wakes behind towed and self-propelled bodies: asymptotic theory. Phys. Fluids 16, 3235–3238.Google Scholar
Batchelor, G. K. 1956 A proposal concerning laminar wakes behind bluff bodies at large Reynolds number. J. Fluid Mech. 1 (04), 388–398.CrossRefGoogle Scholar
Batchelor, G. K. 1967 An Introduction to Fluid Mechanics. Cambridge University Press.Google Scholar
Batchelor, G. K. 1970 The stress system in a suspension of force-free particles. J. Fluid Mech. 41, 545–570.Google Scholar
Blake, J. R. 1971 A spherical envelope approach to ciliary propulsion. J. Fluid Mech. 46, 199–208.Google Scholar
Blanco, A. & Magnaudet, J. 1995 The structure of the axisymmetric high-Reynolds number flow around an ellipsoidal bubble of fixed shape. Phys. Fluids 7 (6), 1265–1274.Google Scholar
Brennen, C. & Winnet, H. 1977 Fluid mechanics of propulsion by cilia and flagella. Annu. Rev. Fluid Mech. 9, 339–398.Google Scholar
Childress, S. 1981 Mechanics of Swimming and Flying. Cambridge University Press.CrossRefGoogle Scholar
Dandy, D. S. & Leal, L. G. 1986 Boundary-layer separation from a smooth slip surface. Phys. Fluids 29 (5), 1360–1366.CrossRefGoogle Scholar
Deen, W. M. 1998 Analysis of Transport Phenomena. Oxford University Press.Google Scholar
Dennis, S. C. R. & Walker, J. D. A. 1971 Calculation of the steady flow past a sphere at low and moderate Reynolds numbers. J. Fluid Mech. 48 (04), 771–789.CrossRefGoogle Scholar
Drescher, K., Leptos, K. C. C., Tuval, I. & Ishikawa, T. 2009 Dancing Volvox: Hydrodynamic bound states of swimming algae. Phys. Rev. Lett. 102, 168101.Google Scholar
Ern, P., Risso, F., Fabre, D. & Magnaudet, J. 2012 Wake-induced oscillatory paths of bodies freely rising or falling in fluids. Annu. Rev. Fluid Mech. 44, 97–121.CrossRefGoogle Scholar
Fabre, D., Auguste, F. & Magnaudet, J. 2008 Bifurcations and symmetry breaking in the wake of axisymmetric bodies. Phys. Fluids 20 (5), 051702.CrossRefGoogle Scholar
Fornberg, B. 1988 Steady viscous flow past a sphere at high Reynolds numbers. J. Fluid Mech. 190, 471–489.CrossRefGoogle Scholar
Gazzola, M., Van Rees, W. M. & Koumoutsakos, P. 2012 C-start: optimal start of larval fish. J. Fluid Mech. 698, 5–18.Google Scholar
Geuzaine, C. & Remacle, J.-F. 2009 Gmsh: A 3-D finite element mesh generator with built-in pre-and post-processing facilities. Intl J. Numer. Meth. Engng 79 (11), 1309–1331.CrossRefGoogle Scholar
Gottlieb, D. & Orszag, S. A. 1977 Numerical Analysis of Spectral Methods: Theory and Applications. vol. 26. SIAM.Google Scholar
Gray, J. 1968 Animal Locomotion. Weidenfeld & Nicolson.Google Scholar
Hallez, Y. & Legendre, D. 2011 Interaction between two spherical bubbles rising in a viscous liquid. J. Fluid Mech. 673, 406–431.CrossRefGoogle Scholar
Hamel, A., Fisch, C., Combettes, L., Dupuis-Williams, P. & Baroud, C. N. 2011 Transitions between three swimming gaits in paramecium escape. Proc. Natl Acad. Sci. USA 108 (18), 7290–7295.Google Scholar
Horowitz, M. & Williamson, C. H. K. 2010 The effect of Reynolds number on the dynamics and wakes of freely rising and falling spheres. J. Fluid Mech. 651, 251–294.CrossRefGoogle Scholar
Hunter, J. D. 2007 Matplotlib: A 2D graphics environment. Comput. Sci. Engng 9 (3), 90–95.CrossRefGoogle Scholar
Ishikawa, T., Simmonds, M. P. & Pedley, T. J. 2006 Hydrodynamic interaction of two swimming model micro-organisms. J. Fluid Mech. 568, 119–160.CrossRefGoogle Scholar
Ishikawa, T., Simmonds, M. P. & Pedley, T. J. 2007 The rheology of a semi-dilute suspension of swimming model micro-organisms. J. Fluid Mech. 588, 399–435.CrossRefGoogle Scholar
Johnson, T. A. & Patel, V. C. 1999 Flow past a sphere up to a Reynolds number of 300. J. Fluid Mech. 378, 19–70.Google Scholar
Jones, E., Oliphant, T. & Peterson, P.2015 SciPy: Open source scientific tools for Python. Available at www.scipy.org.Google Scholar
Jordan, C. E. 1992 A model of rapid-start swimming at intermediate Reynolds number: undulatory locomotion in the chaetognath Sagitta elegans . J. Expl Biol. 163 (1), 119–137.CrossRefGoogle Scholar
Karniadakis, G. E. & Sherwin, S. 2005 Spectral/hp Element Methods for Computational Fluid Dynamics, 2nd edn. Oxford University Press.CrossRefGoogle Scholar
Kern, S. & Koumoutsakos, P. 2006 Simulations of optimized anguilliform swimming. J. Expl Biol. 209, 4841–4857.CrossRefGoogle ScholarPubMed
Khair, A. S. & Chisholm, N. G. 2014 Expansions at small Reynolds numbers for the locomotion of a spherical squirmer. Phys. Fluids 26, 011902.CrossRefGoogle Scholar
Lauga, E. & Powers, T. R. 2009 The hydrodynamics of swimming microorganisms. Rep. Prog. Phys. 72, 096601.Google Scholar
Leal, L. G. 1989 Vorticity transport and wake structure for bluff bodies at finite Reynolds number. Phys. Fluids A 1 (1), 124–131.CrossRefGoogle Scholar
Legendre, D. & Magnaudet, J. 1998 The lift force on a spherical body in a viscous linear shear flow. J. Fluid Mech. 368, 81–126.CrossRefGoogle Scholar
Legendre, D., Merle, A. & Magnaudet, J. 2006 Wake of a spherical bubble or a solid sphere set fixed in a turbulent environment. Phys. Fluids 18 (4), 048102.CrossRefGoogle Scholar
Li, G.-J. & Ardekani, A. M. 2014 Hydrodynamic interaction of microswimmers near a wall. Phys. Rev. E 90, 013010.Google ScholarPubMed
Lighthill, M. J. 1952 On the squirming motion of nearly spherical deformable bodies through liquids at very small Reynolds numbers. Commun. Pure Appl. Maths 5, 109–118.Google Scholar
Lighthill, M. J. 1975 Mathematical Biofluiddynamics. SIAM.CrossRefGoogle Scholar
Lin, Z., Thiffeault, J.-L. & Childress, S. 2011 Stirring by squirmers. J. Fluid Mech. 669, 167–177.Google Scholar
Llopis, I. & Pagonabarraga, I. 2010 Hydrodynamic interactions in squirmer motion: Swimming with a neighbour and close to a wall. J. Non-Newtonian Fluid Mech. 165 (17–18), 946–952.Google Scholar
Magar, V., Goto, T. & Pedley, T. J. 2003 Nutrient uptake by a self-propelled steady squirmer. Q. J. Mech. Appl. Maths 56, 65–91.Google Scholar
Magar, V. & Pedley, T. J. 2005 Average nutrient uptake by a self-propelled unsteady squirmer. J. Fluid Mech. 539, 93–112.CrossRefGoogle Scholar
Magnaudet, J. & Mougin, G. 2007 Wake instability of a fixed spheroidal bubble. J. Fluid Mech. 572, 311–337.Google Scholar
Magnaudet, J., Rivero, M. & Fabre, J. 1995 Accelerated flows past a rigid sphere or a spherical bubble. Part 1. Steady straining flow. J. Fluid Mech. 284, 97–135.CrossRefGoogle Scholar
Matsumoto, G. I. 1991 Swimming movements of ctenophores, and the mechanics of propulsion by ctene rows. Hydrobiologia 216–217 (1), 319–325.Google Scholar
McHenry, M. J., Azizi, E. & Strother, J. A. 2003 The hydrodynamics of locomotion at intermediate Reynolds numbers: undulatory swimming in ascidian larvae (Botrylloides sp.). J. Expl Biol. 206 (2), 327–343.CrossRefGoogle ScholarPubMed
Merle, A., Legendre, D. & Magnaudet, J. 2005 Forces on a high-Re spherical bubble in a turbulent flow. J. Fluid Mech. 532, 53–62.CrossRefGoogle Scholar
Michelin, S. & Lauga, E. 2011 Optimal feeding is optimal swimming for all Peclet numbers. Phys. Fluids 23 (10), 101901.CrossRefGoogle Scholar
Moore, D. W. 1963 The boundary layer on a spherical gas bubble. J. Fluid Mech. 16 (02), 161–176.Google Scholar
Mougin, G. & Magnaudet, J. 2001 Path instability of a rising bubble. Phys. Rev. Lett. 88 (1), 014502.Google Scholar
Natarajan, R. & Acrivos, A. 1993 The instability of the steady flow past spheres and disks. J. Fluid Mech. 254, 323–344.Google Scholar
Pak, O. S. & Lauga, E. 2016 Theoretical models of low-Reynolds-number locomotion. In Fluid-Structure Interactions in Low-Reynolds-Number Flows (ed. Duprat, C. & Stone, H.), chap. 4, pp. 100–167. The Royal Society of Chemistry.Google Scholar
Purcell, E. M. 1977 Life at low Reynolds number. Am. J. Phys. 45, 3–11.Google Scholar
Pushkin, D. O., Shum, H. & Yeomans, J. M. 2013 Fluid transport by individual microswimmers. J. Fluid Mech. 726, 5–25.Google Scholar
Ryskin, G. 1980 The extensional viscosity of a dilute suspension of spherical particles at intermediate microscale Reynolds numbers. J. Fluid Mech. 99 (03), 513–529.CrossRefGoogle Scholar
Stone, H. A. 1993 An interpretation of the translation of drops and bubbles at high Reynolds numbers in terms of the vorticity field. Phys. Fluids A 5 (10), 2567–2569.Google Scholar
Stone, H. A. & Samuel, A. D. T. 1996 Propulsion of microorganisms by surface distortions. Phys. Rev. Lett. 77, 4102–4104.Google Scholar
Subramanian, G. 2010 Viscosity-enhanced bio-mixing of the oceans. Curr. Sci. 98 (8), 1103–1108.Google Scholar
Tamm, S. L. 2014 Cilia and the life of ctenophores. Invertebr. Biol. 133 (1), 1–46.Google Scholar
Thiffeault, J.-L. & Childress, S. 2010 Stirring by swimming bodies. Phys. Lett. A 374 (34), 3487–3490.CrossRefGoogle Scholar
Tomboulides, A. G. & Orszag, S. A. 2000 Numerical investigation of transitional and weak turbulent flow past a sphere. J. Fluid Mech. 416, 45–73.CrossRefGoogle Scholar
Tytell, E. D., Hsu, C.-Y., Williams, T. L., Cohen, A. H. & Fauci, L. J. 2010 Interactions between internal forces, body stiffness, and fluid environment in a neuromechanical model of lamprey swimming. Proc. Natl Acad. Sci. USA 107 (46), 19832–19837.Google Scholar
Vogel, S. 1996 Life in Moving Fluids. Princeton University Press.Google Scholar
Walker, J. A. 2002 Functional morphology and virtual models: physical constraints on the design of oscillating wings, fins, legs, and feet at intermediate Reynolds numbers. Integr. Comp. Biol. 42 (2), 232–242.CrossRefGoogle ScholarPubMed
Wang, S. & Ardekani, A. 2012 Inertial squirmer. Phys. Fluids 24, 101902.CrossRefGoogle Scholar
Zhu, L., Do-Quang, M., Lauga, E. & Brandt, L. 2011 Locomotion by tangential deformation in a polymeric fluid. Phys. Rev. E 83 (1), 011901.Google Scholar
Zhu, L., Lauga, E. & Brandt, L. 2012 Self-propulsion in viscoelastic fluids: pushers versus pullers. Phys. Fluids 24 (5), 091902.Google Scholar